Canvas 行列式与矩阵基础

Posted 2022-08-31 liangklfang

矩阵变换是图形绘制中很重要的一个概念，本部分主要对 Canvas 中牵涉到的矩阵相关知识进行深入的剖析。比如数学中常见的行列式、逆矩阵等等，同时给出了在 Canvas 2D 环境中如何计算逆矩阵的通用方法，通过这部分的学习将有助于后续更好的理解 Canvas 中的矩阵知识。

1.什么是 n 阶行列式

1.1 n 阶行列式的定义

按照一定的规则，由排成正方形的一组(n 个)数(称为元素)之乘积形成的代数和，称为 n 阶行列式。例如，四个数 a、b、c、d 所排成的二阶行式记为:

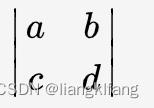
它的展开式为 ad-bc。九个数 a1，a2，a3；b1，b2，b3；c1，c2，c3 排成的三阶行列式记为：

它的展开式为 a1b2c3 + a2b3c1 + a3b1c2 - a1b3c2 - a2b1c3 - a3b2c1。行列式起源于线性方程组的求解，在数学各分支有广泛的应用。在代数上，行列式可用来简化某些表达式，例如表示含较少未知数的线性方程组的解等。

1.2 n 阶行列式的值

1.1 小节讲述了 n 阶行列式的定义，现在假如有如下 n 阶行列式，那么如何求该行列式的值呢？