欠定方程组的最小范数解

Posted 2022-08-30 陆嵩

欠定方程组的最小范数解（超曲面和原点的距离，原点球心球面和超曲面的切点）

今天小白问了我一个问题，我觉得颇有意思，做个记录。

问题描述

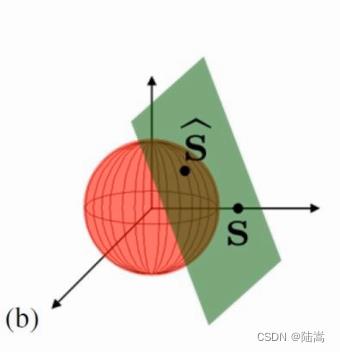
小白：插入一个问题，这个切点怎么求？就是固定超平面Ax=b 怎么求它的最小二范数。

她说得不是很清楚，我再翻译一下。几何的提法是，超平面 $Ax=b$ 到圆心距离是多少？代数的提法是，欠定方程组 $Ax=b$ 的最小范数解是什么？

问题建模

我喜欢代数这个提法。重新描述一下，我们考虑
$$y=Ax$$
这里的 $A\in {\mathbf{R}}^{m\times n}$ 是个 胖矩阵，即 $m<n$。我们不妨假定 $A$ 是行满秩的。
对于这个问题，我们知道这里未知量的个数比方程的个数多，也就是解是存在不唯一的。代数学知识告诉我们，它的解集是
$$x\mid Ax=y=x_p+z\mid z\in \mathcal{N}(A)$$
这里 $x_p$ 是个特解。零空间的维数 $\mathcal{N}(A)=n-m$ 刻画了自由度的数目。那么，我们能否选择一个 $z$ ，使得 $x_p+z$ 的二范数最小呢？

问题解答

这是个经典的计算数学问题了，如果是低于三维的情况，高中的知识很快就能解出来了。高维情况，答案也很简单，他就是
$$x_{\ln }=A^T{\left(A{A}^T\right)}^{-1}y$$
因为 A 是行满秩的，所以 $A{A}^T$ 是可逆的。怎么得到的这个解？对于
$$Ax=b$$
我们令 $x=A^T\bar{x}$，$\bar{x}$ 是个 m 维的。则有
$$x=A^T\bar{x}=A^T(A{A}^T{)}^{-1}b.$$
事实上，这个 $x_{\ln }$ 就是最小范数解，它极小化了如下的优化问题，

minimize $\Vert x\Vert$
subject to $Ax=y$

其中，$x\in {\mathbf{R}}^n$。证明如下：

假定其它解满足 $Ax=y$，那么 $A\left(x-x_{\ln }\right)=0$，且
$$\begin{array}{rl}{\left(x-x_{\ln }\right)}^T{x}_{\ln }& ={\left(x-x_{\ln }\right)}^T{A}^T{\left(A{A}^T\right)}^{-1}y\\ & ={\left(A\left(x-x_{\ln }\right)\right)}^T{\left(A{A}^T\right)}^{-1}y\\ & =0\end{array}$$
也就是说，$\left(x-x_{\ln }\right)\perp x_{\ln }$，那么
$$\Vert x{\Vert }^2={\Vert x_{\ln }+x-x_{\ln }\Vert }^2={\Vert x_{\ln }\Vert }^2+{\Vert x-x_{\ln }\Vert }^2\ge {\Vert x_{\ln }\Vert }^2$$
说明了 $x_{\ln }$ 是范数最小的解。

$A^{†}:=A^T{\left(A{A}^T\right)}^{-1}$ 叫做行满秩胖矩阵 $A$ 的伪逆，实际上是 $A$ 的右逆。

几何观点

画个示意图如下，

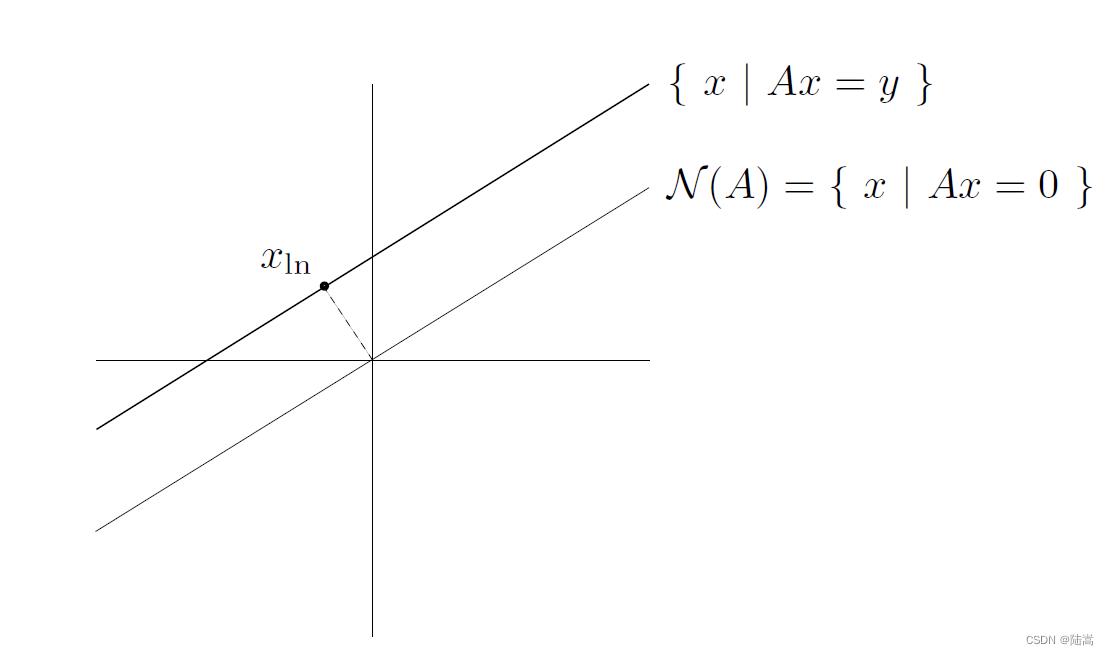
• 这个解垂直于零空间， x ln ⁡ ⊥ N ( A ) x_\\ln \\perp \\mathcalN(A) x欠定方程组的最小范数解

  欠定方程组的最小范数解

  Matlab在线性代数中的应用：求解非齐次线性方程组

  matlab练习程序（椭球拟合）

  稀疏优化L1范数最小化问题求解之基追踪准则(Basis Pursuit)——原理及其Python实现

  稀疏优化L1范数最小化问题求解之基追踪准则(Basis Pursuit)——原理及其Python实现