图的抽象：如何从概念的定义中提取模型？

Posted 2022-08-30 Phodal

最近的业余时间里，一直在研究图相关的领域，顺便构建出 feakin 图形引擎。在研究了 Mermaid、Cytoscape、Drawio/MxGraph/MaxGraph、Excalidraw 等图形库之后，大概写了两个 PoC（概念验证）：

• 数据的处理。即将文本转换为可渲染的数据模型。即结合语法解析、图算法来对数据进行处理。

• 图形的渲染。即基于 Konva.js 的 Canvas 方式来渲染图形。

在这个过程中，因为研究时间比较分散，一些概念相对比较模糊。所以，便想抽空重新梳理一下其中的思路，方便于后续继续研究。

什么是图，什么是图表？

开始之前，我们需要定义一下什么是图（Graph），以及本文所指的图形是什么？我们这里所指的是图是指：

图是计算机科学的一个大主题，可用于抽象表示交通运输系统、人际交往网络和电信网络等。对于训练有素的程序员而言，能够用一种形式来对不同的结构建模是强大的力量之源。—— Steven S. Skiena《算法设计指南》

简单来说，我们这里所指的图是用来表示网络关系的，通常会采用的是节点（Node）来表示实体，使用线条（Edge）来表示关系。诸如于，我们绘制的流程图，便是这里的图；而我们通常所见的曲线图等，可以划到图表里。当然了，要准确区分两者的定义是一件非常困难的事，诸如于 Echarts、D3.js 这一类的图形库， 可以同时表示两种图和图表。

也因此，我们这里说里的图，就是提网络及其关系。

图的模型与概念

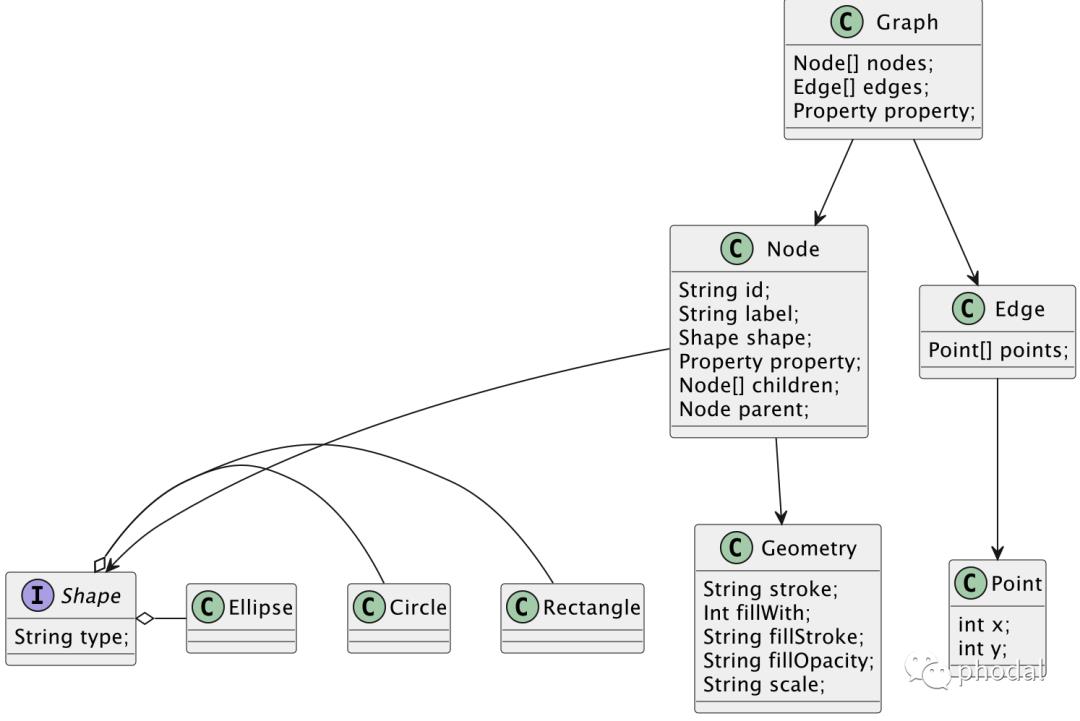
作为一个图领域的新手，在当前的版本里，我构建的模型来源于不同的图形库的实现。而正是这种参考了不同的图形库，使得我对于什么是正确的概念充满了迷惑性。比如，什么是 Geometry（几何），如果从维基百科定义上来说，它主要研究形状（shape）、大小（size）、图形的相对位置（position）、距离（distance）等空间区域关系以及空间形式的度量。

而在 maxGraph（MxGraph 的 TypeScript 版本里），Geometry 下包含了节点（Node）和线条（ Edge），在这时可以认为是他们的子类。

寻找基础的概念：Node 与 Edge

现在，让我们尝试回到标准的定义之下，如果我们基于标准的 Wikimedia 的定义的话，那么 Graph 是这么呈现的：

In mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called vertices (also called nodes or points) and each of the related pairs of vertices is called an edge (also called link or line). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics.

基于它，我们可以构建一个构建出一个基本的图的模型：

• Graph 是一个包含了一系列对象的数据结对，这些对象由表示关系的 Edge（线条）和表示节点的 Node（节点，或者 Vertex，即顶点） 组成。

• Node 可以用 Dot （点）和 Circle （圆圈）的形状来表示。

• Edge 可以用 Line （线）和 Curve（曲线）来表示。

这里的 Dot 和 Circle 可以用 Shape 来进行抽象，而 Line 和 Curve 在实例画之后，就是一系列的 Points（点）。

然后，再让我们打开 Vertex 的定义：

In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another.

在这里，我们又进一步展开了 Node 和 Edge 的定义：

• Node 通常是带有标签的，这里的标签通常是指文本。

• Edge 除了 Line ，还可以带有箭头（arrow），即它是有方向性的。

而如果我们定义的是 Node，那么参考 Node 的定义：

A node is a basic unit of a data structure, such as a linked list or tree data structure. Nodes contain data and also may link to other nodes. Links between nodes are often implemented by pointers. It is a computer connected to the internet that participates in the peer to peer network.

进一步地，因为它是一个树型结构，所以我们需要强化一个 Node 的定义：

• Node 包含 children、parent、depth、degree 等属性。

综上所述，一个 Node 会包含一系列的属性，一个包含大量属性的模型，显然是不利于我们建模的，我们应该怎么办？

引入概念降低认识负载：Geometry

为了更好地描述这些属性，我们就可以考虑引入 Geometry，通过组合的方式解决这个问题。

It is concerned with properties of space such as the distance, shape, size, and relative position of figures.

对于距离、大小、相对位置，我们比较好理解，而 Shape（形状） 同样也是一个非常有意思的概念。

A shape or figure is a graphical representation of an object or its external boundary, outline, or external surface, as opposed to other properties such as color, texture, or material type.

所以 Shape 也需要再次展示，它包含了一些有意思的属性。在我们使用 SVG 或者 Canvas 表示的时候，分别可以对应于：

• Stroke。如 Width 等。

• Fill。如 透明度（Opaciyy）等。

• Scale。缩放

• 等

而从定义上，我们会发现颜色、材质等属性，似乎不应该放在 Shape 中。那么，我们是否需要一些额外的概念来放置它们呢？或者是直接扔到 Node 中，采用 Properties，诸如于 Graph Database 的做法：

Properties are information associated to nodes.

在这时，就会有 Node Properties 和 Edge Properties。在构建了基本的模型之后，就可以将模型可视化出来 。

数据与模型的渲染：Drawing

当我们拿到了模型及其数据之后，就可以对其进行渲染了，而在 Wiki 中 Rendering 讲述的是 3D 图形的渲染，对应于 2D 则是 Graph Drawing。对于绘制来说，我们关注于两点：

• Layout Strategies。布局策略，即各类不同的布局方式。基于布局方式选择不同的算法。

• Renderer。如基于 SVG、Canvas 等的 Renderer。

Layout 策略

关于图算法相关的内容，已经有蛮多的内容可以参考了，也有一系列的代码库可以使用。诸如于：

• Mermaid 采用的是 dagre.js，并使用 dagre-d3 + D3 进行渲染。

• D3.js 也包含了一系列常用的 Layout 策略，如 Force-Layout、Hierarchy-Layout 等。

• Cytoscape.js 也内置了 Breadthfirst、Circle、CoSE 等布局策略，也支持通过扩展的方式来进行。

而随着 AI 的流行，人们也开始在上面探索机器学习的可能性。

Renderer

对于 Renderer 来说，如果我们不加入 Animation 的话，并不存在太复杂的点 —— 只是将数据拿过来，然后在渲染介质上表示出来即可。而如果加上动画的话，就又是一个有意思的问题了 —— 等以后再研究了。

小结

本文主要是针对于自己编码过程中的理解，重新对建模进行了思考。如果你有相关的经验，欢迎留言\\~。

相关的参考内容：

• 《图数据库》

• 《数据分析之图算法》