考研数据结构与算法图论

Posted 2022-08-29 MangataTS

文章目录

• • 一、图的基本概念
  • • 1.1 图的定义
    • 1.2 基本术语
    • • 1.2.1 有向图
      • 1.2.2 无向图
      • 1.2.3 简单图
      • 1.2.4 多重图
      • 1.2.5 完全图
      • 1.2.6 子图
      • 1.2.7 连通、连通分量、连通图
      • 1.2.8 强连通
      • 1.2.9 生成树、森林
      • 1.2.10 顶点的度
      • 1.2.11 边权和网
      • 1.2.12 稠密、稀疏图
      • 1.2.13 路径、路径长度、回路
      • 1.2.14 简单路径、简单回路
      • 1.2.15 距离
      • 1.2.16 有向树
  • 二、图的存储结构
  • • 2.1 邻接矩阵
    • 2.2 邻接表
    • 2.3 十字链表
    • 2.4 邻接多重链表
  • 三、图的遍历方法
  • • 3.1 广度优先搜索（BFS）
    • 3.2 深度优先搜索（DFS）
  • 四、图的基本应用
  • • 4.1 最小生成树
    • 4.2 最短路径
    • 4.3 有向无环图描述表达式
    • 4.4 拓扑排序
    • 4.5 关键路径
  • 五、错题
  • • 选择题

一、图的基本概念

1.1 图的定义

图 G 由顶点集 $V$ 边集 $E$ 组成，记为 $G=(V,E)$ ， 其中 $V(G)$ 表示图 $G$ 中顶点的有限非空集；
$E(G)$ 表示图 $G$ 中顶点之间的关系 （边） 集合。 若 $V=V_1,V_2，\dots ，V_n$，则用 $|V|$ 叫表示图中顶点的个数，也称图 $G$ 的阶， $E=(u,v)|u\in V,v\in V$，用 $|E|$ 表示图 $G$ 中边的条数。

注意：图的顶点集 $V$ 一定为非空，而图的边集 $E$ 可能为空

1.2 基本术语

1.2.1 有向图

图中的边集是由方向的，例如有一个从点 $A$ 到 $B$ 的有向边，那么我们从 $A$ 点可以到达 $B$ 点，而不能从 $B$ 点到达 $A$ 点，这样就是一个有向边，在这条边中点 $A$ 被称为 弧尾 ，而点 $B$ 被称为 弧头 ，我们通常用这样的符号来记录这条边：<A,B>

1.2.2 无向图

很显然没有方向的边和顶点集构成的图就为无向图，按照上面的情况，在无向图中顶点之间是互相连通的，即若有一个点 $A$ 到点 $B$ 的边，从 $B$ 出发也是能到达 $A$ 点的，我们通常使用这样的符号来记录这条边：(A,B)

1.2.3 简单图

一个图 $G$ 若满足：

• ①不存在重复边
• ②不存在顶点到自身的边，则称图 $G$ 为简单图

1.2.4 多重图

若图 $G$ 中某两个结点之间的边数多于一条，又允许顶点通过同一条边也和自己关联，则 $G$ 为多重图。多重图的定义和简单图是相对的

1.2.5 完全图

• 在一个顶点数量为 $n$ 的无向图中，若边的数量为 $\frac{(n-1)\times n}{2}$ ，则该无向图为完全图
• 在一个顶点数量为 $n$ 的有向图中，若边的数量为 $(n-1)\times n$ ，则该有向图为完全图

1.2.6 子图

设有两个图 $G=(V,E)$ 和 $G^{\prime }＝(V^{\prime },E^{\prime })$， 若 $V^{\prime }$是 $V$ 的子集，且 $E^{\prime }$是 $E$ 的子集，则称 $G^{\prime }$ 是 $G$ 的子图，若满足 $V^{\prime }=V$ 且 $E^{\prime }\subset E$ 那么子图 $G^{\prime }$ 为 $G$ 的生成子图

注意：并非 $V$ 和 $E$ 的任何子集都能构成 $G$ 的子图，因为这样的子集可能不是图， 即 $E$ 的子集中的某些边关联的顶点可能不在这个 $V$ 的子集中

1.2.7 连通、连通分量、连通图

关于连通方面的定义都是基于无向图的

• 连通：在无向图中若从顶点 $u$ 到顶点 $v$ 有路径存在，那么称 $u$ 和 $v$ 是连通的
• 连通图：若无向图中任意两点是连通的，那么这个无向图就称为连通图，否则称为非连通图
• 连通分量：对于一个连通图而言，其连通分量只有一个就是其本身，而对于非连通图而言，连通分量有多个，其每一个子图（或者称为极大联通子图）都是一个连通分量

很显然一个 $n$ 个点的连通图最少有 $n-1$ 条边（即后面提到的生成树），最多有 $\frac{(n-1)\times n}{2}$ 个边

这里再补一下 极小连通子图 的定义：一个顶点为 $n$ 的子图的边数为 $n-1$ （其实后面也能知道这其实是生成树的定义） ，就称其为极小连通子图，很显然这样的子图也是一个极大连通子图，因为它是一个连通分量。

例如，对于下面的这个非连通图，其连通分量有三个：

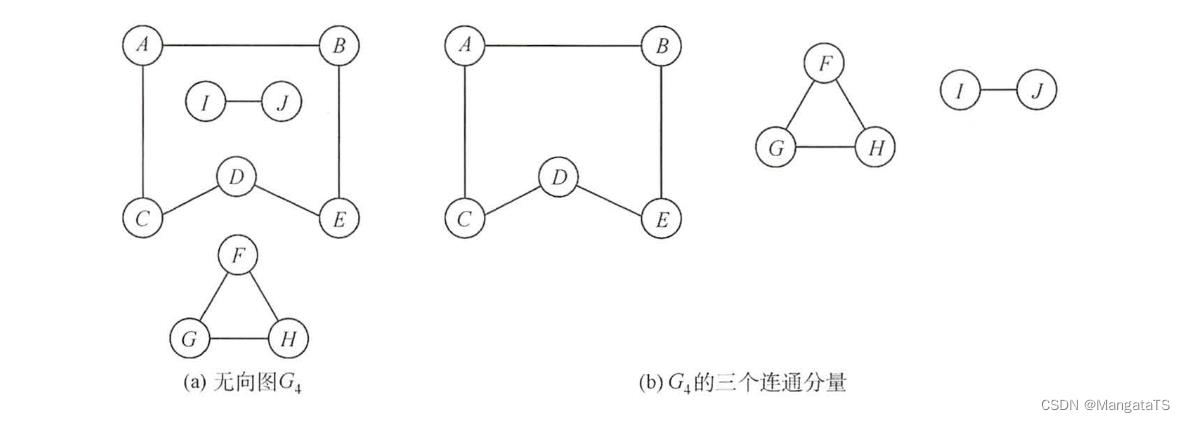
1.2.8 强连通

关于强连通方面的定义都是基于有向图的

• 强连通：在有向图中，若从顶点 $v$ 到顶点 $w$ 和从顶点 $w$ 到顶点 $v$ 之间都有路径 ，则称这两个顶点为强连通的
• 强连通图：若有向图中任意两点之间都是强连通的，那么称这个有向图为强连通图，否则称为非强连通图
• 强连通分量：对于一个强连通图而言，其强连通分量就是本身，而对于一个非强连通图而言，其极大强连通子图就为该非强连通分量（在子图中任意两点仍满足强连通）

例如，对于如下的非强连通图，其中点 $A$ 和 $B$ 构成的子图就为极大联通子图，即强连通分量，而点 $C$ 和 $D$ 构成的子图则不是强连通分量

1.2.9 生成树、森林

生成树、森林一般是基于无向图的

连通图的生成树是包含图中全部顶点的一个极小连通子图，即一个 $n$ 个点的连通图中有 $n-1$ 条边

很显然这样的连通图，如果减去一条边就会形成非连通图，而若是加上一条边，则会形成回路

例如，下图中的连通图就为一个生成树：

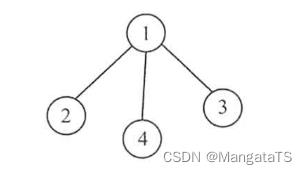
而生成森林其实就是多个连通子图都是极小连通子图（生成树），那么就称这个森林为生成森林，例如下图中左边森林为生成森林，而右边的森林不是连通森林：

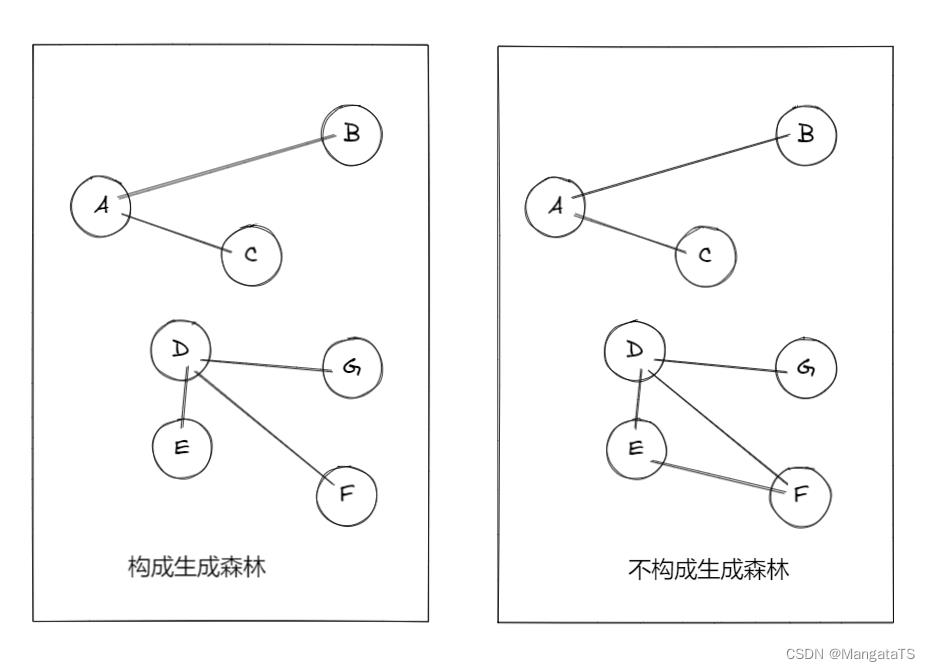
1.2.10 顶点的度

• 无向图：对于无向图而言，顶点的度就是和该顶点相连接的边数
• 有向图：对于有向图而言，指向该顶点的边数称为入度，而从该顶点指出的边数称为出度

• 无向图的全部顶点的度之和等于两倍的边数
• 有向图的全部顶点的出度等于全部顶点的入度等于边数

1.2.11 边权和网

在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值。 这种边上带有权值的图称为带权图，也称网 。
网中通常分为， $AOV$ 网和 $AOE$ 网

• $AOV$ 网：没有权值，或者权值都相同，主要是在于点与点之间的先后关系
• $AOE$ 网：有权值，每一个点称为事件，而边称为活动

1.2.12 稠密、稀疏图

• 稠密图：点数较大，而边数较少的图称为稀疏图
• 稠密图：点数较小，而边数较多的图称为稠密图

一般来说当图 $G$ 满足 $|E|<|V|lo{g}_2|V|$ 的时候，可以将图G定义为稀疏图，反之则为稠密图

1.2.13 路径、路径长度、回路

• 路径：顶点 $V_u$ 到顶点 $V_v$ 的顶点序列 $V_p,V_{i1},V_{i_2},\dots \dots ,V_u$ 称为这两点的路径
• 路径长度：路径上边的数目称为路径长度
• 回路：起点和终点相同的非 $0$ 路径长度的路径称为回路

1.2.14 简单路径、简单回路

• 简单路径：在路径的顶点序列中顶点不重复的路径称为简单路径
• 简单回路：除了起点和终点相同外其余顶点不重复的回路称为简单回路

1.2.15 距离

从顶点 $u$ 出发到顶点 $v$ 的最短路径若存在，则此路径的长度称为从 $u$ 到 $v$ 的距离 。 若从 $u$ 到