30个题型+代码(冲刺2023蓝桥杯)(下)
Posted 千帐灯无此声
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了30个题型+代码(冲刺2023蓝桥杯)(下)相关的知识,希望对你有一定的参考价值。
👂 咱们结婚吧(心动版) - 1个球 - 单曲 - 网易云音乐
又一个被社会磨平棱角灰头土脸的失败者平庸人罢了
-----------------------------------分界线----------------------------
2023/5/13~8/13持续更新
(上)(1条消息) 30个题型+代码(冲刺2023蓝桥杯)(上)_码龄?天的博客-CSDN博客
(中) 30个题型+代码(冲刺2023蓝桥杯)(中)_码龄?天的博客-CSDN博客
AcW需要付费的题,可以考虑上洛谷,New Oj找替代,或者花点钱
目录
👊(二)1701: [NewOJ Contest 1] 01卡片
🍎注意
上篇博客写完第4个题型已经31063字了,卡得写不动了,敲完一行字等10秒才显示
每10个题型写一个博客,分为上中下末4个博客,15万字收尾
后续再补充剩下两个博客地址
(上)(1条消息) 30个题型+代码(冲刺2023蓝桥杯)(上)_码龄?天的博客-CSDN博客
(中)(11条消息) 30个题型+代码(冲刺2023蓝桥杯)(中)_蓝桥杯题型_千帐灯无此声的博客-CSDN博客
🌼前言
前缀和√,差分√,二分√,双指针√,递归√,递推√,BFS√,DFS,Dijkstra, Floyd,质数筛,最大公约数,背包dp,线性dp,区间dp,组合计数,快速幂,哈希√,并查集√,博弈论
每个类型第一题来自AcWing蓝桥杯集训-每日一题
1,花5块钱
2,上洛谷找替代 / 原题
题型
前缀和,差分,二分,双指针,递推,递归,并查集,哈希,单调队列,
KMP,Trie,BFS,DFS,拓扑排序,Dijkstra,Floyd,最小生成树,
最近公共祖先,二分图,筛质数,最大公约数,快速幂,组合计数,博弈论,
背包DP,线性DP,区间DP,树型DP,树状数组,线段树,矩阵乘法
如果你想冲省一,拿22年A组为例,你得拿60分,也就是2道填空题 + 4道编程题
5 + 5 + 10 + 10 + 15 + 15
省赛需要掌握的有:
前缀和,差分,二分,双指针,递归,递推,BFS,DFS,Dijkstra, Floyd,质数筛,最大公约数,背包dp,线性dp,区间dp,组合计数,快速幂,哈希,并查集,博弈论
围绕省赛需要掌握的类型,针对性地下手
先给大家看个时间复杂度(来源于AcWing)

🌼二十一,筛质数
🌼二十二,最大公约数
🌼二十三,快速幂
🌼二十四,组合计数
🌼二十五,博弈论
🌼二十七,线性DP
👊知识分析
动态规划其实就是,通过记住求过的解,来节省时间(通过避免重复计算已经算过的东西)
通常用 一维 / 二维 / 三维 数组保存求过的解(这里的解是,通过决策保存有可能达到最优的局部解) ------关于开几维数组,看你需要几个变量
1,线性dp就是普通dp / 裸dp,实际上就是递推 + 一个数组(保存过程中需要的数据)
2,动态规划与分治的区别:
(1)动态规划:子问题重叠;分治:子问题相互独立
比如斐波那契数列,更适合用dp来做,因为F(7) = F(6) + F(5),
而F(6) = F(5) + F(4),容易发现,F(5)在分治里被计算了2次
而dp用一维数组dp[i]将F(i)保存起来,后续需要子问题的解,直接从数组找就行
-----(2)同时,如果子问题的最优解能代表整个问题的最优解,才适用于动态规划
dp解斐波那契数列
#include<iostream>
using namespace std;
int dp[40];
int fibo(int n)
if(n <= 1) return n;
for(int i = 2; i <= n; ++i)
dp[i] = dp[i - 2] + dp[i - 1];
return dp[n];
int main()
dp[0] = 0, dp[1] = 1;
int n;
cin>>n;
cout<<fibo(n);
return 0;
分治解斐波那契数列
#include<iostream>
using namespace std;
int fibo(int n)
if(n <= 1) return n;
return fibo(n - 1) + fibo(n - 2);
int main()
int n;
cin>>n;
cout<<fibo(n);
return 0;
显而易见,分治比dp少了个一维数组保存中间的结果,但是慢了上百倍,具体参考这几个博客
然而,当我做了2题后发现,动规不一定要数组保存中间结果,它也可以是通过递推/递归/分治等来实现,只要能避免子问题的重复计算,提高速度就行
→ (20条消息) 分治法与动态规划求解斐波那契数列_kingdragonfly的博客-CSDN博客
→ (20条消息) 动态规划与分治法异同_动态规划和分治法的区别_白给、少年的博客-CSDN博客
→ 动态规划和分治法的区别 - Frank_Allen - 博客园 (cnblogs.com)
我在学习dp过程看的其他博客(强烈建议全看一遍,不做题最多2小时就吸收完了!)

DP核心👆
→ (9条消息) 算法-动态规划 Dynamic Programming--从菜鸟到老鸟_HankingHu的博客-CSDN博客
→ (9条消息) 经典中的经典算法:动态规划(详细解释,从入门到实践,逐步讲解)_动态规划算法_god 's favored one的博客-CSDN博客
→ (12条消息) C++之动态规划(动态规划入门)_DJS编程小白的博客-CSDN博客
→ (10条消息) C++动态规划详解_Godvvvvvvv的博客-CSDN博客
→ (9条消息) 告别动态规划,连刷40道动规算法题,我总结了动规的套路_Hollis Chuang的博客-CSDN博客
看完这9个博客,请再来看3个视频
视频中的思路都差不多,先摆出方法论(dp的步骤),再结合方法论(套路/模板),套到每一道题目上
dp的步骤
一,确定 dp[i] 或者 dp[i][j] 中 dp[i] 和 i( dp[i][j] 和 i , j )的具体含义(状态),比如斐波那契数列中,dp[i] 表示第 i 个斐波那契数,i 表示第几个
二,找递推公式(通过最后一步,将问题转化成子问题)
三,如何初始化(你要初始化多少个,初始化的值是什么,同时避免越界)
四,确定遍历顺序(一维前往后后往前;二维从左上角,右下角,甚至是中间等开始遍历)
五,打印dp数组(cout或者printf的形式debug)
B站10万浏览量以上的up讲的都差不多,关于dp,就4个步骤,就是以上的步骤👆
dp的题型
一,计数
·走到右下角的方式有多少种
·选出k个数和为sum的可能数
·青蛙每次跳n格,跳到最后一格的方案数
二,求最大最小值
·左上角 -> 右下角路径的最大数字和
·最长上升子序列长度
三,求存在性
·取石子,先手是否必胜
·能不能选出k个数使得和为sum
·青蛙能否跳到最后一个格子
观察上述dp题型,求的都是种类数,个数,数字的和,长度,true/false,都是一个结果,而非路径
如果要输出路径,不用dp(只能输出结果而已),一般用dfs或bfs
1,
从此再也不怕动态规划了,动态规划解题方法论大曝光 !| 理论基础 |力扣刷题总结| 动态规划入门_哔哩哔哩_bilibili
2,
手把手带你入门动态规划 | 对应力扣(leetcode)题号:509.斐波那契数_哔哩哔哩_bilibili
3,
2小时超详细推理过程,建议看看👇
【动态规划专题班】ACM总冠军、清华+斯坦福大神带你入门动态规划算法_哔哩哔哩_bilibili
然后,,可以开始做题了,循序渐进,由简到繁
👊(一)1112: 平面分割
标签:基础题,动态规划
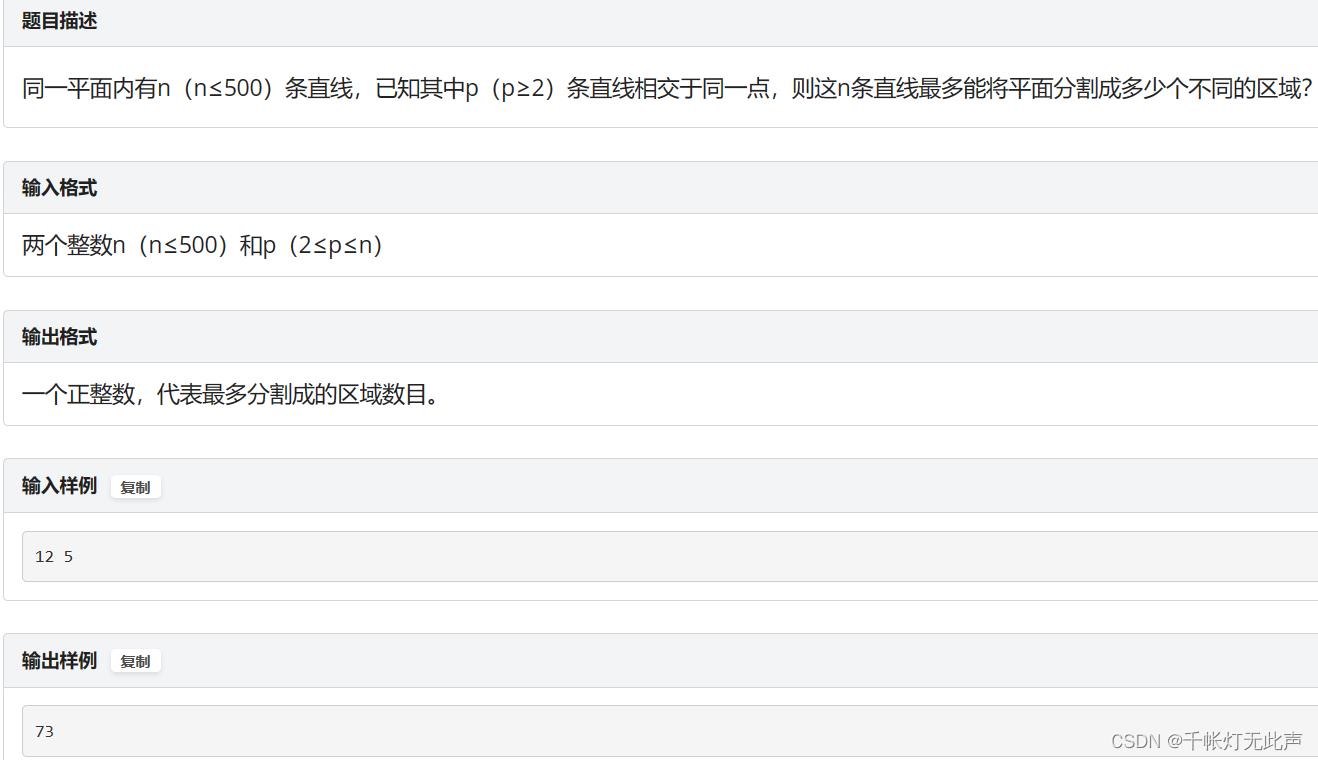
思路
1,确定状态(含义):
这里我们用dp[i]表示前 i 条直线分割的最大区域数,i 表示用到了 i 条直线
怎么分割才是最大区域数呢,新的直线和所有旧的直线都相交就行,也就是不平行
2,找递推公式:
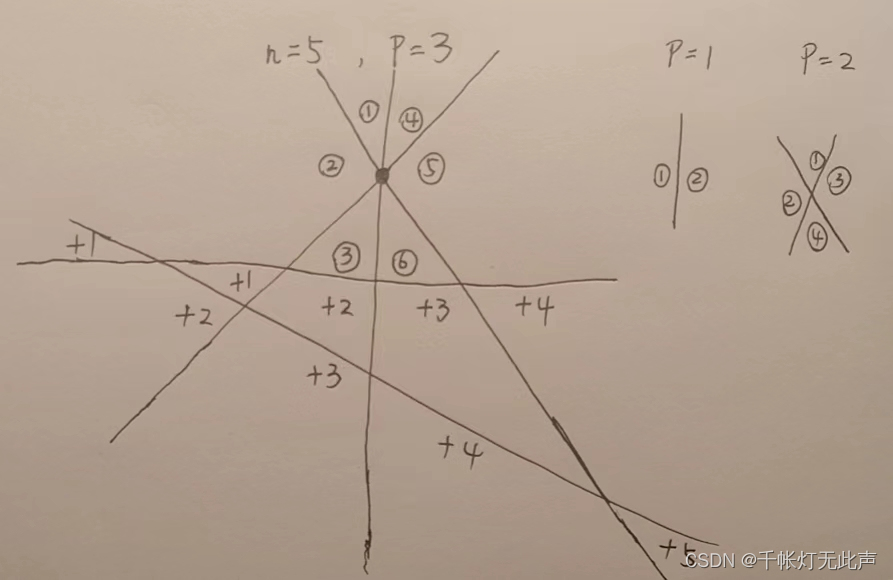
由上图,dp[p] = 2 * p是显然的,后续增加第 i 条直接,就增加 i 个区域
dp[i] = dp[i - 1] + i;3,初始状态当然就是dp[p] = 2 * p;
4,遍历顺序从前到后
AC 代码1
#include<iostream>
using namespace std;
int dp[510], n, p;
int main()
cin>>n>>p;
dp[p] = 2 * p;
for(int i = p + 1; i <= n; ++i)
dp[i] = dp[i - 1] + i;
cout<<dp[n];
return 0;
AC 代码2
用int型变量代替了dp[]
#include<iostream>
using namespace std;
int sum, n, p;
int main()
cin>>n>>p;
sum = 2 * p;
for(int i = p + 1; i <= n; ++i)
sum += i;
cout<<sum;
return 0;
👊(二)1701: [NewOJ Contest 1] 01卡片
P1701 - [NewOJ Contest 1] 01卡片 - New Online Judge (ecustacm.cn)
标签:基础题,模拟,动态规划
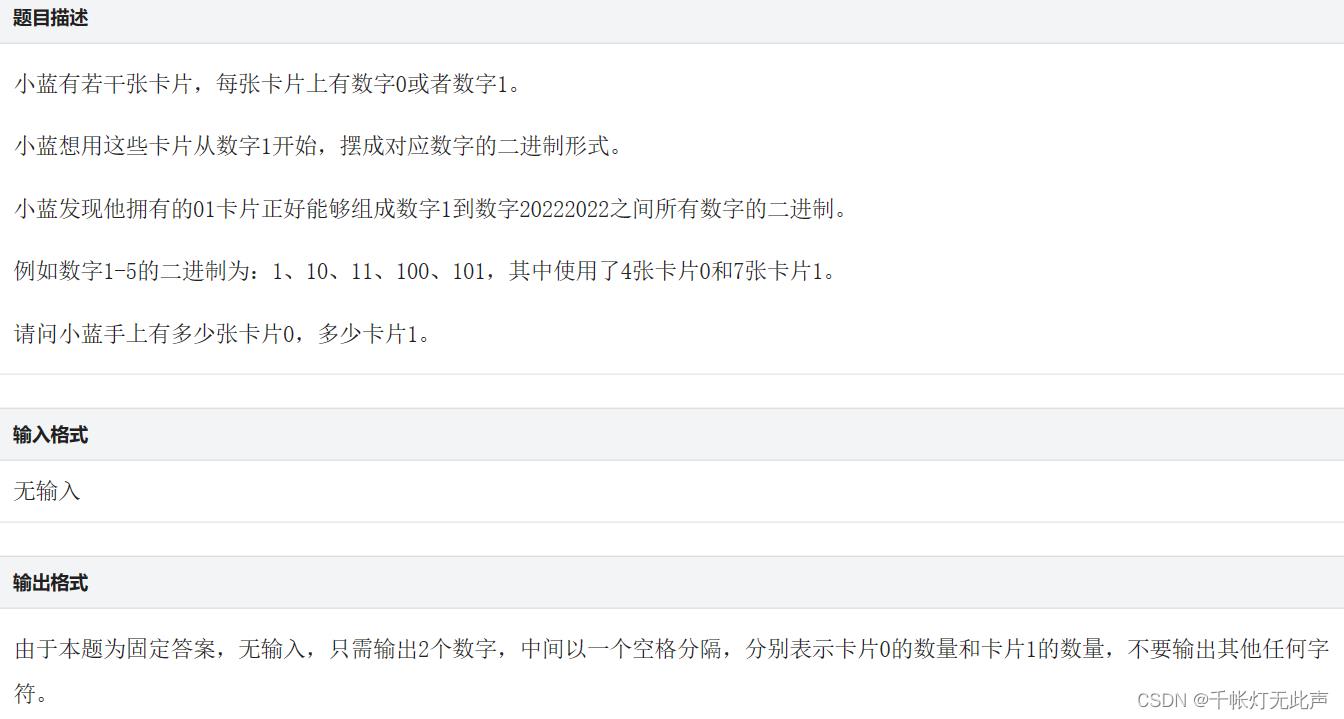
🌳AC 暴力 O(nlogn)
本地编译器代码
#include<iostream>
using namespace std;
long long sum0, sum1;
//10转2后含有的0和1
void binary(int x)
while(x)
if(x % 2 == 0)
sum0 += 1;
else if(x % 2 == 1)
sum1 += 1;
x /= 2;
int main()
for(int i = 1; i <= 20222022; ++i)
binary(i);
cout<<sum0<<" "<<sum1;
return 0;
测试了2组数据,修改 i <= 5和 i <= 10的输出都正确了,可以提交
提交代码
#include<iostream>
using namespace std;
int main()
cout<<230401142<<" "<<241595002;
return 0;
🌳AC 递推 O(n)
将佬的思路加进来,主要为了加深对动规的理解,要我写也写不出来
不过我写成了递推
fzl的思路很清奇,反正像我一样的大多数普通人,估计是想不到,除非经过大量训练
思路来源博客B题 (96条消息) NewOJ 2022 Contest 1题解_傅志凌的博客-CSDN博客
首先
dp[i]表示前i个数二进制表示中,0的个数和;记s[i]表示i的二进制中0的个数
dp[6] = (s[1] + s[3] + s[5]) + (s[2] + s[4] + s[6])
s[1] + s[3] + s[5] = s[0] + s[1] + s[2] = dp[2]
s[2] + s[4] + s[6] = 3 + s[1] + s[2] + s[3]
即dp[6] = 3 + dp[2] + dp[3]
由此扩展到所有偶数
dp[n] = n / 2 + dp[n / 2] + dp[n / 2 - 1]
类似对于奇数
dp[n] = n / 2 + 2 * dp[n / 2] --------以上除法均向下取整
类似对于1的个数。。。。
然而我写出来的,看似想用动规,实际上只是递推
如果判断子问题重复计算呢,自己模拟下递归树,看看是否一直有重复就行
从2遍历到20222022,显然,中间很多步骤并不需要
#include<iostream>
using namespace std;
int dp0[20222032], dp1[20222032];
int main()
//初始化dp数组
dp0[1] = 0, dp1[1] = 1;
//递推
for(int i = 2; i <= 20222022; ++i)
if(i % 2 == 0) //偶数
dp0[i] = dp0[i / 2] + dp0[i / 2 - 1] + i / 2;
dp1[i] = dp1[i / 2] + dp1[i / 2 - 1] + i / 2;
else //奇数
dp0[i] = 2 * dp0[i / 2] + i / 2;
dp1[i] = 2 * dp1[i / 2] + i / 2 + 1;
cout<<dp0[20222022]<<" "<<dp1[20222022];
return 0;
🌳AC 动规 O(logn)
这个是fzl的原代码
动规的思路,递推来实现,容易发现,这个思路没有重复计算,比如20222022直接到了10111011
中间计算的每一步,都是需要的,不像前面的暴力或者遍历+递推,重复计算了大量子问题
#include<bits/stdc++.h>
using namespace std;
int Zero(int x)
if(x <= 1)return 0;
if(x & 1) return 2 * Zero(x / 2) + x / 2;
else return Zero(x / 2) + Zero(x / 2 - 1) + x / 2;
int One(int x)
if(x <= 1)return x;
if(x & 1) return 2 * One(x / 2) + x / 2 + 1;
else return One(x / 2) + One(x / 2 - 1) + x / 2;
int main()
cout<<Zero(20222022)<<" "<<One(20222022)<<endl;
return 0;
👊(三)1114: 放苹果
P1114 - 放苹果 - New Online Judge (ecustacm.cn)
标签:基础题,动态规划,递归
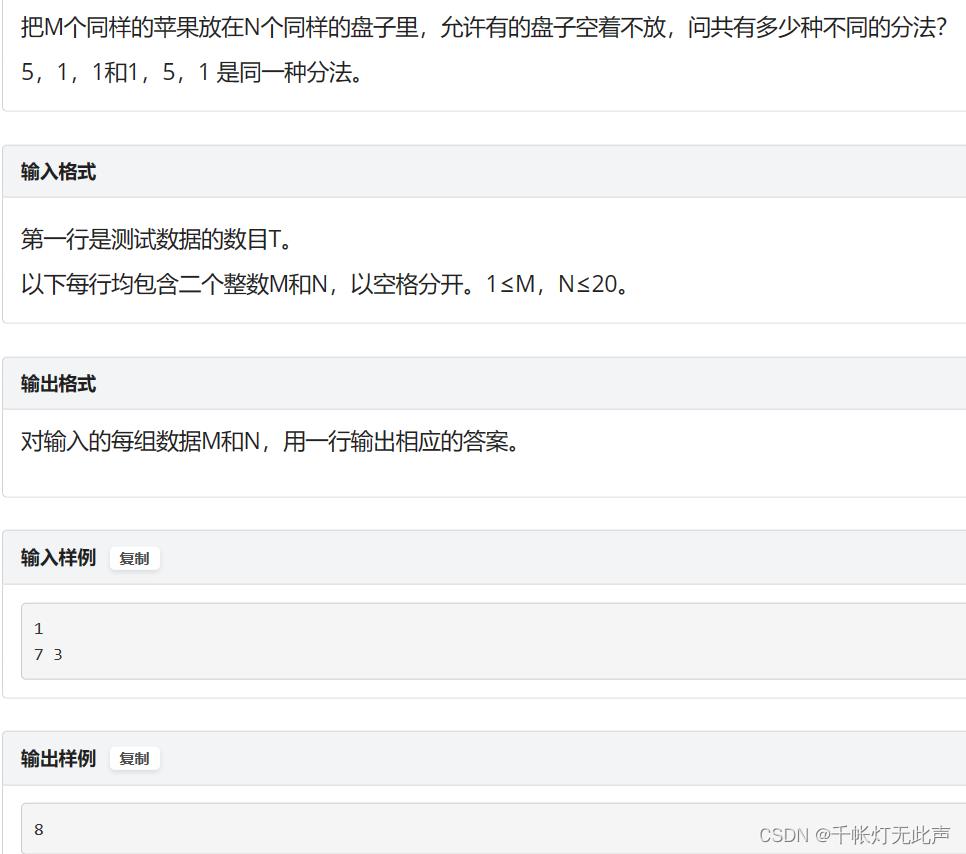
AC很容易,找找题解,模仿着一写就以为自己会了
难得是把这题摸透一点,比如,
为什么自己的代码,时间复杂度那么高(O(2^n, n^3, n^2)),而别人的那么低(O(logn, n, nlogn))
如果数据量达到1e4,1e5你还能AC吗,如果题目换个条件,你还会做吗?
如何改进?每一行代码该怎么解释?过一周再遇到一道类似的,你能在半小时内AC吗?
思路
dp[i][j]表示将 i 个苹果 放入 j 个盘子(状态)
dp[i][j] = dp[i][j - 1] + dp[i - j][j](递推式)
dp[i][1] = 1, dp[0][j] = 1;(初始化)
前往后遍历(遍历方式)
分析
首先注意题目字眼
1,“同样的苹果盘子” --> 5, 1, 1和1, 5, 1一样,所以不能用dfs搜索
2,“允许有空的盘子” --> 这句话影响了递推式怎么写
主要解释下递推式和初始化
假设此时有 i 个苹果,j 个盘子,i 个苹果放入 j 个盘子的方案数,可以分成两部分思考
等于将 i 个苹果放入 j - 1 个盘子 加上 先在 j 个盘子,每个盘子放一个苹果,再将剩下
i - j个苹果放入 j 个盘子的方案数,写出来就是dp[i][j - 1] + dp[i - j][j]
---------------------------------------------------------
再解释下初始化
初始化是由递推式推导过来的,先写出递推式,才能进一步找到初始条件
解释:将任何数量的苹果放入一个垃圾桶中或没有垃圾桶可放苹果时的方案数都为 1
由于递推式中 j 的变化只有 j - 1的情况,显然,当 j == 1只剩一个盘子时,所有的苹果只能放进这一个盘子,是一种情况,所以dp[i][1] = 1
第二个就是,i 的变化只有 i - j,i - j == 0的情况显然存在,此时剩0个苹果,所以也只有一种可能(假设此时 i = 1, j = 100,第一步就是变成 i = 1, j = 1,下一步直接就 i = i - j直接=0了,所以是1种)
初始化的状态表示递归的终点
对比
本题中第二个代码使用了动规的思路,将子问题的解保存到二维数组中,通过递推得到当前问题的解,避免了重复计,也减小了问题的规模
而第一个代码虽然简单易懂,但复杂度指数级别,数据量大就会TLE
🌳AC 递推 O(2^n)
这个是指数级复杂度,与dp只有一个记忆化的距离,其实dp和记忆化是一个东西,说到底是一种思想
复杂度高达2^n,因为每个苹果都有2种选择,进 / 不进盘子
#include<iostream>
using namespace std;
int m, n;
//x个苹果放入y个垃圾桶
int dfs(int x, int y)
if(x < y)
return dfs(x, x); //去掉多于垃圾桶无影响
if(x == 0 || y == 1) //0个苹果或1个垃圾桶, 有递推式判断初始状态
return 1;
return dfs(x, y - 1) + dfs(x - y, y);
int main()
int t;
cin>>t;
while(t--)
cin>>m>>n;
cout<<dfs(m, n)<<endl;
return 0;
🌳AC 动规 O(mn)
这个可能数据量到10^4甚至10^5都不会超时
#include<iostream>
using namespace std;
int dp[30][30], m, n, t;
int main()
cin>>t;
while(t--)
cin>>m>>n;
//初始状态, 尽量从0开始初始化
for(int i = 0; i <= m; ++i) dp[i][1] = 1; //剩1种可能
for(int j = 0; j <= n; ++j) dp[0][j] = 1; //同上
//递推式
for(int i = 0; i <= m; ++i) //i个苹果放入j个垃圾桶
for(int j = 1; j <= n; ++j)
if(i < j) dp[i][j] = dp[i][i]; //去掉多余盘子
else dp[i][j] = dp[i][j - 1] + dp[i - j][j];
//else不要漏
cout<<dp[m][n]<<endl;
return 0;
👊(四)P1115 最大子段和
P1115 最大子段和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
标签:动态规划,分治,递推,线性数据结构,普及-
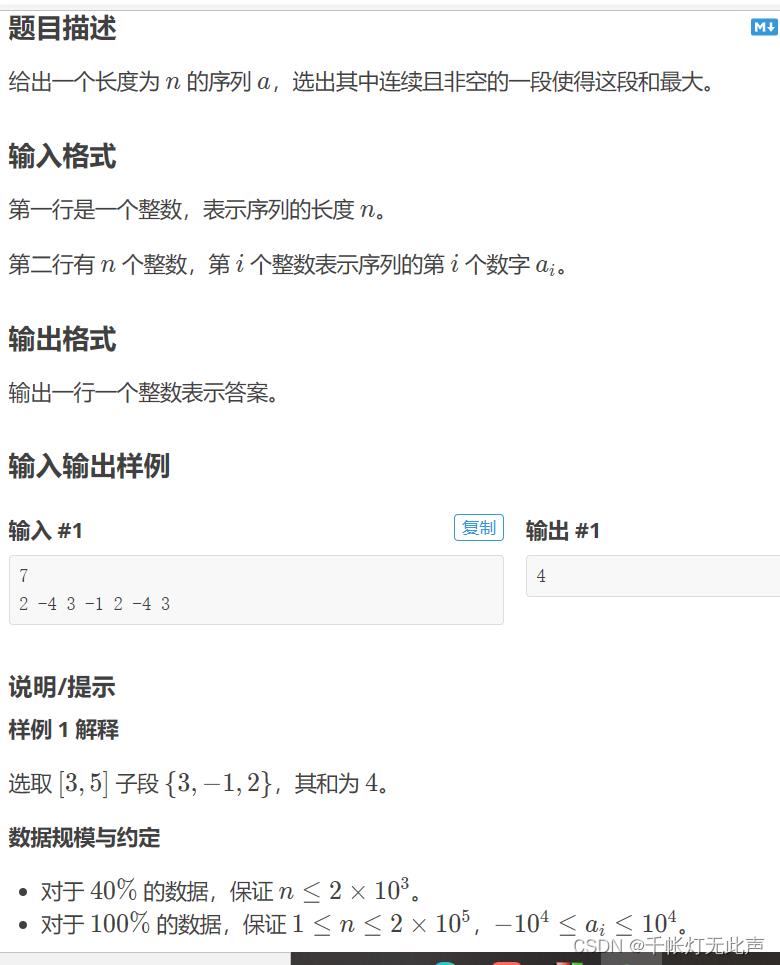
你可以认为这题是第(五)题的铺垫,实际上我先做了第(五)题才回来写这题
本题采用3种解法,1,双指针 2,前缀和 3,动态规划
知识点
双指针的认识还很浅,,,缺乏练习,真遇到大概率做不出来
→ 前缀和 & 差分 - OI Wiki (oi-wiki.org)
🌳AC 双指针
#include<iostream>
#include<cstdio> //scanf()
using namespace std;
int a[200010], ans = -1e9, sum;
int main()
int n;
scanf("%d", &n);
for(int i = 0; i < n; ++i)
scanf("%lld", &a[i]);
//ans保存最大子段和, sum保存当前子段和
//i是右边界, sum代替了左边界的作用
for(int i = 0; i < n; ++i)
if(sum < 0) sum = a[i]; //这里是= a[i]而不是0, 存在负数
else sum += a[i];
ans = max(ans, sum);
cout<<ans;
return 0;
🌳AC 前缀和
注意
1,前缀和可以在输入时求出
2,显而易见,ans初始值设置要小于-1e4,关键是int Min = 0;这个不能设置为尽可能小的负数
否则无法取到第1至第i个元素的最小前缀和,第1个会取不到
#include<iostream>
#include<cstdio> //scanf()
using namespace std;
int a[200010], s[200010], ans = -1e9; //s[]前缀和
int main()
int n;
scanf("%d", &n);
//读入的同时得到前缀和
for(int i = 1; i <= n; ++i)
scanf("%d", &a[i]);
s[i] = s[i - 1] + a[i];
int Min = 0; //Min是前缀和在[0, i]的最小值
//边取子段和边得到当前最小前缀和
for(int i = 1; i <= n; ++i)
ans = max(ans, s[i] - Min);
Min = min(Min, s[i]);
cout<<ans;
return 0;
动规思路
1,状态
dp[i]表示以a[i]结尾的最大子段和
2,递推式(也称状态转移)
dp[i] = max(dp[i - 1] + a[i], a[i]);
3,初始
dp[0] = 0(假设a[i]从1开始输入)
4,遍历
从前往后
🌳AC 动规
#include<iostream>
using namespace std;
int dp[200010], a[200010], ans = -1e9;
int main()
int n;
cin>>n;
for(int i = 1; i <= n; ++i)
cin>>a[i];
dp[0] = 0;
//dp[i]表示a[i]结尾的最大子段和
for(int i = 1; i <= n; ++i)
dp[i] = max(dp[i - 1] + a[i], a[i]);
//遍历找出1~n最大子段和
for(int i = 1; i <= n; ++i)
ans = max(ans, dp[i]);
cout<<ans;
return 0;
👊(五)1051. 最大的和
标签:DP,线性DP,简单,前后缀分解

🌳AC 50% O(n^2)暴力
Max函数每遍历一次就是n,主函数中再遍历一次分界点也是n,所以复杂度O(n^2),对于30*5e4*5e4,已经达到了7.5 * 10^10 >> 10^8,所以Time Limit
注意,考虑到结果可能小于0,因为两个子段必然是存在的,如果全为负数...
所以代码第8和30行,都应初始化为-1e9(虽说-1e4也都AC了,但是往大了初始化安全)
#include<iostream>
#include<cstdio> //scanf()
using namespace std;
int a[50010], t, n, ans;
int Max(int x)
int sum1 = 0, sum2 = 0, ans1 = -1e9, ans2 = -1e9;
//判断前半段
for(int i = 0; i <= x; ++i)
if(sum1 < 0)
sum1 = 0;
sum1 += a[i];
ans1 = max(ans1, sum1);
//判断后半段
for(int i = x + 1; i < n; ++i)
if(sum2 < 0)
sum2 = 0;
sum2 += a[i];
ans2 = max(ans2, sum2);
return ans1 + ans2; //返回最大两字段和
int main()
scanf("%d", &t);
while(t--)
scanf("%d", &n);
ans = -1e9;
for(int i = 0; i < n; ++i)
scanf("%d", &a[i]);
//分界点i,
for(int i = 0; i < n - 1; ++i)
ans = max(ans, Max(i));
cout<<ans<<endl;
return 0;
🌳AC 动规 O(n)
看完y总的思路,发现其实对一段的处理,和前面的暴力差不多
然而有2段,方法是预处理下前缀最大和,后缀最大和,第一次接触这种方法
解析在注释里
思路
1,先确定状态,也就是注释中的
dp[i]是a[i]结尾的最大子段和
g[i]是a[0]到a[i]最大子段和
h[i]是a[i]到a[n - 1]最大子段和
2,找递推式
说下预处理前缀的,dp[i] = max(dp[i - 1] + a[i], a[i]),注意最后是a[i]而不是0
3,初始状态
我们根据递推式推初始
预处理前缀:
初始i == 1,i - 1 == 0,g[0]表示a[0]到a[0]的最大子段和,就是a[0],dp[0]表示a[0]到a[0]的最大子段和,也是a[0],所以dp[0] = a[0], g[0] = a[0]
预处理后缀:
当i = n - 1,i + 1 == n,由于输入a[]从0开始的,考虑到存在负数,为了保证取到想要的max值,我们需要将dp[n]和h[n]都设为-1e9(-1e4就能过)
4,遍历顺序,在初始状态中说完了
AC 代码
其实第21行初始化为-1e4即可,因为单个数最小才-10000,
只是最后的ans初始化需要-1e9,-50000*10000 = -5e8
#include<iostream>
#include<cstdio> //scanf()
using namespace std;
int a[50010], g[50010], h[50010]; //输入数组,前缀数组,后缀数组
int dp[50010], t, n;
//dp[i]是a[i]结尾的最大子段和
int main()
scanf("%d", &t);
while(t--)
scanf("%d", &n);
for(int i = 0; i < n; ++i)
scanf("%d", &a[i]);
//预处理前缀, g[i]是a[0]到a[i]最大子段和
dp[0] = a[0], g[0] = a[0];
for(int i = 1; i < n; ++i)
dp[i] = max(dp[i - 1] + a[i], a[i]);
g[i] = max(dp[i], g[i - 1]);
//预处理后缀, h[i]是a[i]到a[n - 1]最大子段和
dp[n] = -1e9, h[n] = -1e9;
for(int i = n - 1; i >= 0; --i)
dp[i] = max(dp[i + 1] + a[i], a[i]);
h[i] = max(dp[i], h[i + 1]);
//分界点i
int ans = -1e9;
for(int i = 0; i < n; ++i)
ans = max(g[i] + h[i + 1], ans);
cout<<ans<<endl;
return 0;
空间优化
补充个用变量sum代替dp数组,对空间进行优化的代码,只进行了细微的修改
为什么能去掉dp[]呢,看看上面代码第17和23行,dp[i]只和它的上一个相关
比如假设一个
dp[i] = dp[i - 1] + a[i];
//或者
dp[i] = dp[i + 1] + a[i];显然可以表示成(当然这里看遍历顺序,sum分别代表dp里的-1和+1,都是上一个的意思)
sum = sum + a[i];
//或者
sum = sum + a[i];AC 代码2
😃只需要把所有dp出现的地方,全换成sum就行了
#include<iostream>
#include<cstdio> //scanf()
using namespace std;
int a[50010], g[50010], h[50010]; //输入数组,前缀数组,后缀数组
int t, n, sum;
//dp[i]是a[i]结尾的最大子段和
int main()
scanf("%d", &t);
while(t--)
scanf("%d", &n);
for(int i = 0; i < n; ++i)
scanf("%d", &a[i]);
//预处理前缀, g[i]是a[0]到a[i]最大子段和
sum = a[0], g[0] = a[0];
for(int i = 1; i < n; ++i)
sum = max(sum + a[i], a[i]);
g[i] = max(sum, g[i - 1]);
//预处理后缀, h[i]是a[i]到a[n - 1]最大子段和
sum = -1e9, h[n] = -1e9;
for(int i = n - 1; i >= 0; --i)
sum = max(sum + a[i], a[i]);
h[i] = max(sum, h[i + 1]);
//分界点i
int ans = -1e9;
for(int i = 0; i < n; ++i)
ans = max(g[i] + h[i + 1], ans);
cout<<ans<<endl;
return 0;
对比下空间(当然,空间优化只在面试考,算法比赛只看时间复杂度)
 ----------->>>>
----------->>>>
👊(六)895. 最长上升子序列
标签:动态规划,线性DP,最长上升子序列,简单

注意,它没说连续,做动规的题一定要抠字眼,每个字眼都会对递推式产生影响,甚至有些字眼导致无法用dp解决问题
1,明确状态
错误思路:dp[i]表示前 i 个元素中,递增子序列(不一定连续)的最大长度
这样你很难写的出递推式
正确思路:dp[i]表示以第 i 个元素结尾的递增子序列的最大长度
递推式:dp[i] = max(dp[j] + 1, dp[i])
其中 i 是外层循环的,j 是内层循环,内层循环从 第 0 个元素遍历到第 i - 1 个元素,
如果a[j] < a[i],说明可以dp[j] + 1,最后dp[i]取到前面dp[j]的最大值 + 1
2,初始化
显而易见,一个元素时,子序列的长度都为1,所以将dp[i]全初始化为1
这样,最后求结果,只需要遍历一遍dp数组找到最大值
这一步可以放在前面的二层循环里
----------------------------------------------------------
思路参考这个博客:(7条消息) 最长上升子序列(动态规划)_syc_36的博客-CSDN博客
其实还有一种贪心 + 二分,O(nlogn)的方法...感兴趣的自己试试
3,代码
即使 n <= 1e4 还是可以做的,如果到了 n <= 1e5,只能贪心 + 二分了
额外的测试
8
8 7 2 1 2 5 1 7
4有个坑,ans记得初始化为1,ans = 0的话,当输入这个会输出0,因为避开了两层for循环
1
1
0AC DP O(n^2)
#include<iostream>
using namespace std;
int dp[1010], a[1010], ans = 1, n;
int main()
cin>>n;
for(int i = 0; i < n; ++i)
cin>>a[i]; //读入序列
dp[i] = 1; //初始化dp数组
for(int i = 1; i < n; ++i)
for(int j = 0; j < i; ++j)
if(a[i] > a[j])
dp[i] = max(dp[j] + 1, dp[i]);
ans = max(ans, dp[i]);
cout<<ans;
return 0;
🌼二十六,背包DP
👂 Edamame (ft. Rich Brian) - bbno$/Rich Brian - 单曲 - 网易云音乐
不打竞赛,只是准备大厂面试的话,搞清楚01背包和完全背包就够了
因为力扣据说只有01背包和完全背包的题
01背包更是基础中的基础,完全和多重背包,都是在01的基础上进化来的
先区分下01,完全,多重背包
01背包:n种物品,每种物品只有1个(即每个物品只能选0次或1次)
完全背包:n种物品,每种物品无限个
多重背包:n种物品,每种物品的个数,各不相同
🦆01背包知识
视频
👇(这2个视频01背包讲的很清楚)
1,
带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili
2,
带你学透01背包问题(滚动数组篇) | 从此对背包问题不再迷茫!_哔哩哔哩_bilibili
👆
(下面这个视频补充理解)
博客
→ 背包 DP - OI Wiki (oi-wiki.org)
思路
1,状态确定
dp[i][j]表示只能放前 i 个物品的前提下,容量为 j 的背包的最大总价值
(或者说,假设下标从0开始,表示下标为[0, i]之间的物品,任取,放进容量为 j 的背包...)
(如果从1开始,就是下标为[1, i]之间的物品...)
2,递推式
分两步讨论
(1)不放物品 i :dp[i][j] = dp[i - 1][j],表示(剩余)容量不变,从只能放前 i 个物品 -->
只能放前 i - 1个物品
(2)放物品 i :dp[i][j] = dp[i - 1][j - weight[i]] + value[i]
所以在两者中取最大值,dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
(后面熟悉后,weight[i] --> w[i],value[i] --> v[i])
3,初始化
 凑合着看把
凑合着看把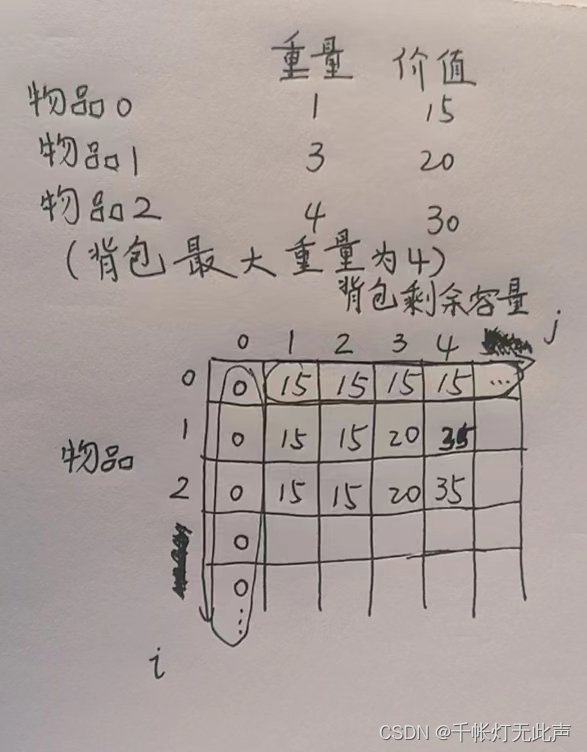
显然,对于二维我们只需初始化第一列和第一行,第一列初始化为0,第一行从背包容量大于等于weight[0]开始,要初始化为value[0]
如何得出上述初始化的呢?
当然是根据递推式以及画图来推的,递推式dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])
i - 1表示正上方,加上个j - w[i],就是左上方,所以当前的dp[][]来自上一行的两个方向,为保证后续dp[][]能实现,只需初始化第一列和第一行
再说下二维 --> 一维,也就是滚动数组
二维正 / 逆序遍历都可以,而且先遍历物品( i )还是背包( j )都行
但是一维只能逆序遍历
解释:二维数组利用的是左上方和正上方的数据,不存在覆盖,所以正向 / 反向遍历都可以
但是转变为一维数组后,正向遍历会覆盖左边数据,所以得反着来(可以去第2个视频看看)
倒叙遍历,保证一维dp[]中,每个物品最多被添加一次
滚动数组递推式:dp[j] = max(dp[j], dp[j - w[i]] + v[i]),把 i 部分去掉就行
🦆完全背包知识
-----------------------------分界线------------------------------
👊(一)2. 01背包问题
标签:背包DP,模板,简单

01背包模板题
我先用二维dp[][]试试会不会MLE(Memory Limit Exceeded)
再用一维dp[]做
第一次敲完,样例对了,又测
蓝桥杯刷题冲刺 | 倒计时13天
🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾
文章目录
1.母牛的故事
-
题目
链接: [递归]母牛的故事 - C语言网 (dotcpp.com)
有一头母牛,它每年年初生一头小母牛。每头小母牛从第四个年头开始,每年年初也生一头小母牛。请编程实现在第n年的时候,共有多少头母牛?
输入格式
输入数据由多个测试实例组成,每个测试实例占一行,包括一个整数n(0<n<55),n的含义如题目中描述。
n=0表示输入数据的结束,不做处理。输出格式
对于每个测试实例,输出在第n年的时候母牛的数量。
每个输出占一行。样例输入
2 4 5 0样例输出
2 4 6 -
第一次 AC 50%
#include<bits/stdc++.h> using namespace std; int main() int n; while(cin>>n) int sum=0; if(n==0) return 0; for(int i=1;i<=n;i++) if(i<=4) sum+=1; else sum+=i-3; cout<<sum<<endl; return 0;枚举了前几个数,找的规律是错的
-
第二次 AC 50% + 超时 50%
#include<bits/stdc++.h> using namespace std; int f(int n) if(n<=4) return n; return f(n-2)+f(n-3)+f(n-4); int main() int n; while(scanf("%d",&n)) if(n==0) return 0; cout<<f(n)<<endl; return 0;递归+规律,第二次递归的规律又找错了
-
第三次 AC 50% + 50% 超时
#include<bits/stdc++.h> using namespace std; int f(int n) if(n<4) return n; return f(n-1)+f(n-3); int main() int n; while(scanf("%d",&n)&&n) //记住这个,当输入0时,跳出循环 cout<<f(n)<<endl; return 0;这次 规律对,但还是 超时
-
第四次 AC 100%
#include<bits/stdc++.h> using namespace std; int main() int n; while(scanf("%d",&n)&&n) int a[60]; a[1]=1,a[2]=2,a[3]=3; for(int i=4;i<=n;i++) //使用数组递归 a[i]=a[i-1]+a[i-3]; cout<<a[n]<<endl; return 0; -
反思
找规律的题:
不要局限在前后相邻的数,不要只找一组,就直接把规律定下来,多找几组
找规律题中+递归,一开始根本没有往这方面想
How
- 找规律,发散思维,很有可能有递归,看看前后几个数之间的关系
- 递归函数,可能会超时,考试的时候,就直接使用 数组来代替函数
2.魔板
-
题目
在魔方风靡全球之后不久,Rubik先生发明了它的简化版――魔板。魔板 由8个同样大小的方块组成,每个方块颜色均不相同,可用数字1-8分别表示。任一时刻魔板的状态可用方块的颜色序列表示:从魔板的左上角开始,按顺时针方 向依次写下各方块的颜色代号,所得到的数字序列即可表示此时魔板的状态。例如,序列(1,2,3,4,5,6,7,8)表示魔板状态为:
1 2 3 4
8 7 6 5
对于魔板,可施加三种不同的操作,具体操作方法如下:
A: 上下两行互换,如上图可变换为状态87654321
B: 每行同时循环右移一格,如上图可变换为41236785
C: 中间4个方块顺时针旋转一格,如上图可变换为17245368
给你魔板的初始状态与目标状态,请给出由初态到目态变换数最少的变换步骤,若有多种变换方案则取字典序最小的那种。输入格式
每组测试数据包括两行,分别代表魔板的初态与目态。
输出格式
对每组测试数据输出满足题意的变换步骤。
样例输入
12345678 17245368 12345678 82754631样例输出
C AC -
第一次 AC 0%
#include<bits/stdc++.h> using namespace std; const int N=1010; int d[N]; string FA(string a) string b=a; a[0]=b[4],a[1]=b[5],a[2]=b[6],a[3]=b[7]; a[4]=b[0],a[5]=b[1],a[6]=b[2],a[7]=b[3]; return a; string FB(string a) string b=a; a[0]=b[3],a[1]=b[0],a[2]=b[1],a[3]=b[2],a[4]=b[6]; a[5]=b[5],a[6]=b[4],a[7]=b[7]; return a; string FC(string a) string b=a; a[0]=b[0],a[1]=b[5],a[2]=b[1],a[3]=b[3]; a[4]=b[4],a[5]=b[6],a[6]=b[2],a[7]=b[7]; return a; void bfs(string st,string over) queue<string> q; q.push(st); unordered_map<string,string> mp; while(q.size()) auto now=q.front(); q.pop(); if(now==over) cout<<mp[now]<<endl; return ; string ss; for(int i=1;i<=3;i++) switch(i) case 1: ss=FA(now); if(!mp.count(ss)) q.push(ss); mp[ss]=mp[now]+'A'; break; case 2: ss=FB(now); if(!mp.count(ss)) q.push(ss); mp[ss]=mp[now]+'B'; break; case 3: ss=FB(now); if(!mp.count(ss)) q.push(ss); mp[ss]=mp[now]+'C'; break; int main() string a,b; while(cin>>a>>b) bfs(a,b); return 0;一开始,框架都写出来,但是输出 转换的路径写不出来,忘记咋写了
好像是倒推,前几天写过,题解中的是用的 STL 里面的 map
哪里出错了,还没有看出来,他没有输出
-
题解
#include<bits/stdc++.h> using namespace std; // 定义两个变量s和f,代表起点状态和终点状态,其值由输入读入 string s, f; // 操作A函数,将输入状态x按照操作A的规则进行变换 string A(string x) string s = x; for (int i = 0; i < 4; i++) swap(s[i], x[7 - i]); swap(s[i + 4], x[3 - i]); return s; // 操作B函数,将输入状态x按照操作B的规则进行变换 string B(string x) string s = x; s[0] = x[3], s[1] = x[0]; s[2] = x[1], s[3] = x[2]; s[4] = x[5], s[5] = x[6]; s[6] = x[7], s[7] = x[4]; return s; // 操作C函数,将输入状态x按照操作C的规则进行变换 string C(string x) string s = x; s[1] = x[6], s[2] = x[1]; s[5] = x[2], s[6] = x[5]; return s; // 广搜函数,使用map进行去重,记录操作序列 void bfs() unordered_map<string, string>mp; // 哈希表,用于存储操作序列 queue<string>q; // 队列,用于存储待搜索状态 q.push(s); // 将初始状态入队 while (!q.empty()) // 只要队列不为空,就继续搜索 string now = q.front(); // 取出队首元素 q.pop(); // 将队首元素出队 if (now == f) // 当达到终点状态,输出操作序列 cout << mp[now] << endl; return; // 搜索结束 string ts; // 操作后的状态 // 按照题目要求,A、B、C操作依次搜索,保证字典序最小 for (int i = 0; i < 3; i++) // 依次搜索ABC操作,保证字典序最小 switch (i) case 0: // A操作 ts = A(now); // 对当前状态进行A操作 if (!mp.count(ts)) // 如果操作后的状态不在哈希表中 q.push(ts); // 将操作后的状态入队 mp[ts] = mp[now] + 'A'; // 更新哈希表,存储操作序列 break; case 1: // B操作 ts = B(now); // 对当前状态进行B操作 if (!mp.count(ts)) // 如果操作后的状态不在哈希表中 q.push(ts); // 将操作后的状态入队 mp[ts] = mp[now] + 'B';// 更新哈希表,存储操作序列 break; case 2://C操作 ts = C(now); // 对当前状态进行B操作 if (!mp.count(ts)) // 如果操作后的状态不在哈希表中 q.push(ts); // 将操作后的状态入队 mp[ts] = mp[now] + 'C';// 更新哈希表,存储操作序列 break; int main() while (cin >> s >> f) bfs(); return 0; -
反思
通过三种不同的转化状态+最少变化步骤,我们可以确定是 BFS
对于我来说,这个题的难点不在于确定最少的步数是多少,而是输出路径
-
学到了使用 switch 执行不同的函数,我差点就使用函数数组了TvT
-
借助了 map 去重+输出路径,学到了
之前我以为路径都必须倒推,很麻烦,map 真的好用
我们再研究一下,路径的记录,再刷一两道题这个类型的题
-

以上是关于30个题型+代码(冲刺2023蓝桥杯)(下)的主要内容,如果未能解决你的问题,请参考以下文章

