基于simulink的Active anti-islanding-AFD主动反孤岛模型仿真

Posted 2022-08-06 fpga和matlab

目录

一、理论基础

二、案例背景

1.问题描述

2.思路流程

三、部分MATLAB程序

四、仿真结论分析

五、参考文献

---

一、理论基础

       l一个性能完善的光伏并网发电系统，需要各种保护措施保证用户的人身安全，同时防止设备因意外而造成的损坏。由于光伏发电系统和电网并联工作，因此光伏发电系统需能及时检测出电网故障并切断其与电网的连接。如果不能及时发现电网故障，就会出现光伏发电系统仍向局部电网供电的情形，从而使本地负载仍处于供电状态，造成设备损坏和人员伤亡。这种现象被称为孤岛效应。

       目前孤岛检测主要分为被动式检测和主动式检测两种。被动式检测是利用电网断电瞬间，逆变器输出功率与局部负载功率不平衡造成的逆变器输出端电压值和频率变化作为孤岛效应检测的依据。其具有检测方法简单，对系统运行无干扰等优点。但是如果在电网停电的瞬间，逆变器输出功率与局部负载功率达到平衡，该方法将失去作用。 

      主动式检测是在系统工作中，对逆变器输出电流、频率或相位施加一定的扰动信号，并对其进行检测。如果电网正常，因电网的巨大平衡作用，逆变器输出不受扰动信号的影响;一旦电网出现故障，这些扰动量就会在逆变器输出端逐步累计，直至超出规定范围，从而反映出电网故障。与被动式检测方法相比，主动式检测方法具有精度高，检测盲区小的优点。但当局部电网存在多个分布式能源系统时，主动式检测效果下降，严重时甚至无效。
        被动式检测主要有电压频率检测、相位检测、频率检测三种方法，在实际中均有一定的应用。但是由于被动式孤岛检测方法对逆变器输出功率与负载功率是否匹配有较高的要求，因此存在较大的检测盲区。所以在此不做详细的描述。
       其中，主动频率偏移(Active Frequency Drift．AFD)孤岛检测方法的思想是通过锁相环(PLL)确定公共点电压的频率和相位．调整光伏逆变器输出电流的给定频率。使电流频率比公共点电压频率略高或略低。若电流半波已完成而电压过零点未到。则强制电流给定为零。直到电压过零点触发到来。电流才开始下一个半波。

       AFD的稳态频率应使负载相角满足如下关系

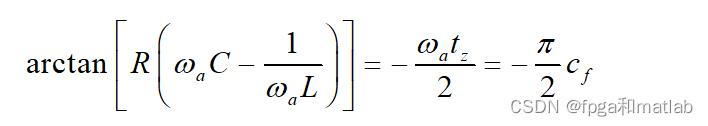
式中tz为电流过零点超前（或滞后）电压过零点的时间间隔。 cf为AFD的截断系数,T为电压周期。

二、案例背景

1.问题描述

首先，这个电力系统，我们做如下的设置，即：

230V/50Hz，单相（single phase or 1 phase）。

    然后，仿真的具体要求为：

负载：小型电网 single phase 1kW grid-connected PV systems 

根据 IEEE 1547 standard 对反孤岛的要求

·Voltage： 240V ± 10%， 

·frequency：50Hz ± 1%

·Quality Factor, Qf:  Qf < 2.5 (Qf = 0 , 0.02,0.04, … , 2.4)

·Required Islanding detection time: tdetect<0.2s  and isolated to the load

·THD: <5%

2.思路流程

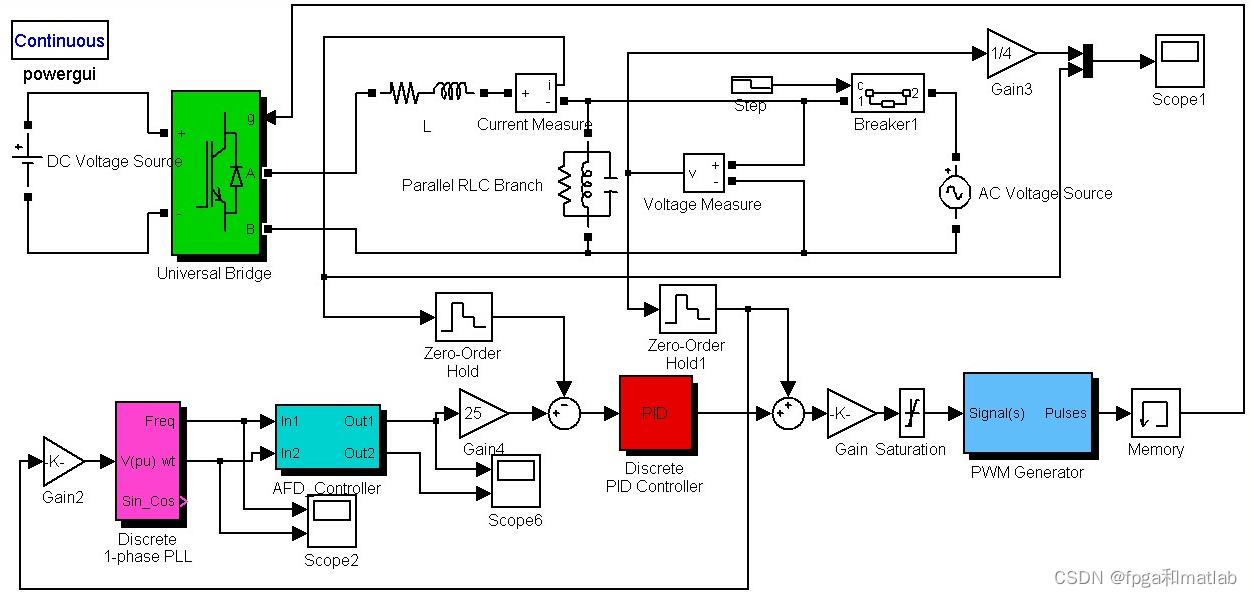
       整个反孤岛模型，采用simulink进行建模，在matlab2010b中，建立仿真模型，其中AFD算法则采用S函数进行设计，并封装为AFD模块供simulink调用。

三、部分MATLAB程序

AFD的S函数部分程序如下：

function [sys,x0,str,ts]=mdlInitializeSizes
%定义全局变量
global f_i;            
global f_vo;
global f_v_hb;
global f_v_lb;
global theta_i;
global theta_vo;
global isIslanding;
global num0;
global num1;
global step;
global step1;
global k;

%以下指标根据IEEE1547来取值
f_i        = 50; %电流频频率
f_vo       = 50; %电压频率
theta_i    = 0;  %电流相位
theta_vo   = 0;  %电压相位
isIslanding= 0;  %非孤岛效应
num0       = 0;
num1       = 0;
k          = 10;
step1      = 0.5;
f_v_hb     = 50;
f_v_lb     = 50;

%获得系统默认的系统参数变量sizes    
sizes                = simsizes;
%连续状态的个数
sizes.NumContStates  = 0;
%离散状态的个数
sizes.NumDiscStates  = 0;
%输出变量的个数
sizes.NumOutputs     = 2;
%输入变量的个数
sizes.NumInputs      = 2;
%布尔变量，表示有无直接馈入。1表示有，0便是没有
sizes.DirFeedthrough = 1;
%采样时间个数，s函数支持多采样系统
sizes.NumSampleTimes = 1;  
%将结构体sizes赋值给sys
sys                  = simsizes(sizes);
%初始变量状态
x0                   = [];
%系统保留值，必须为空
str                  = [];
%采样周期变量
ts                   = [1e-4 0];
 
function sys=mdlOutputs(t,x,u)
%定义全局变量
global f_i;            
global f_vo;
global f_v_hb;
global f_v_lb;
global theta_i;
global theta_vo;
global isIslanding;
global num0;
global num1;
global step;
global step1;
global k;

%锁相环输出
theta_vo=u(2);
%电压相位为0时更新频率
if abs(theta_vo) < 0.04	
  %数字锁相环输出的电压频率
  f_vo=u(1);    
end

%判断是否不是孤岛效应
if(isIslanding==0)	
    %并网电压相位是否过零  
    if abs(theta_vo)<0.04    
    %判断并网电压频率是否越界，根据1547规定，1%的调整，所以就是正负0.5Hz
          if (f_vo>50.5) || (f_vo<49.5)	
                sys         = [0 0];
                %如果超出则为孤岛检测到了
                isIslanding = 1;
          else         
              f_vo = u(1);
              if(f_v_lb < f_vo) 
                 num0=0;
              end
              if(f_vo   < f_v_hb)
                 num1=0;   
              end

              if (f_vo>=50)
                    num1=num1+1;
                    if(num1>0)
                      step=k*step1;
                    else
                      step=step1;
                    end   
                    f_i    = f_vo+step; 
                    f_v_hb = f_i;
              else
                    num0=num0+1;
                    if(num0>0)
                      step=k*step1;
                    else
                      step=step1;
                    end    
                    f_i    = f_vo-step;
                    f_v_lb = f_i;
              end      
          theta_i=theta_vo;
          end
    else
        if(pi-theta_i<0.03) && (pi-theta_vo>0.03) 
            theta_i=pi;
        elseif(2*pi-theta_i<0.03) && (2*pi-theta_vo>0.03) 
            theta_i=2*pi;                    
        elseif (pi-theta_vo<0.03) && (pi-theta_i>0.03)
            theta_i=pi;
        elseif (2*pi-theta_vo<0.03) && (2*pi-theta_i>0.03)
            theta_i=2*pi;
        else
            theta_i=theta_i+2*pi*f_i*1e-4;
        end
    end
    %非孤岛输出正弦波
    sys(1)=sin(theta_i);
else
    %孤岛输出零
    sys(1)=0;
end

sys(2)=f_vo;

AFD的simulink整体模型如下：

四、仿真结论分析

    运行simulink仿真的结果进行显示，具体的仿真结果如下所示：

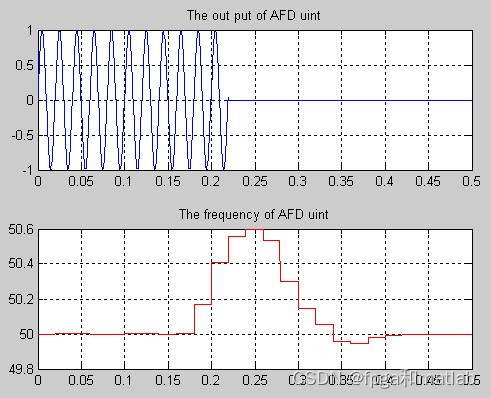
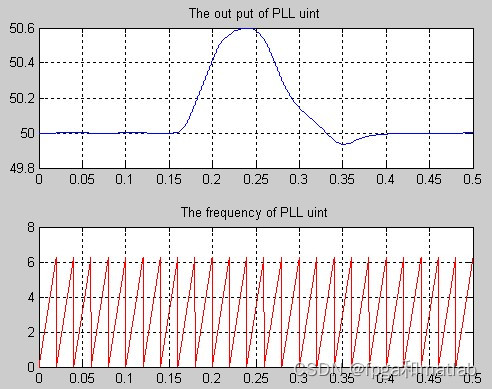
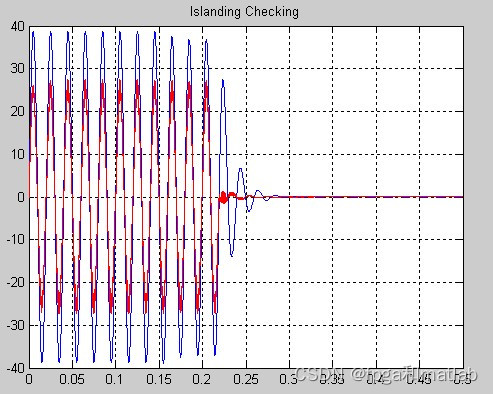
       从前面的仿真结果可知，采用AFD这种主动反孤岛的方式，系统能够较快的检测到孤岛，但是同时AFD对系统的波形影响较大。

五、参考文献

[1] Velasco D ,  Trujillo C , Garcerá, G, et al. An Active Anti-Islanding Method Based on Phase-PLL Perturbation[J]. IEEE Transactions on Power Electronics, 2011, 26(4):1056-1066.A2-12