Google面试题原理解析 12个乒乓球其中有1个次品，用天平称重3次找出

Posted 2022-08-05 AI架构师易筋

1. 题目

“在12个小球里有一个次品，重量与其他11个球不同。用一个没有砝码的天平，称3次，保证找到那个次品，并且区分出次品是轻还是重呢？”

这个问题看似简单，做起来还真不容易。

误区：也许有人说：我可以用二分法，先把球均分成两堆，上天平比较，找到重的一堆，次品就在这里。再把重的一堆均分成两堆，上天平比较…这样，每次就能把球去掉一半，就能最快找到次品啦！这样子会很慢。

2. 原理解析

分析一下原理: 12个球，每个球有重了，轻了2中状态，也就是一共有12 x 2 = 24 种状态。称一次实际上可以区分3中状态，平衡，重，轻。
比如把球分成3堆A,B,C。称的结果解析：

1. 平衡。A == B, A和B中都是好球, 也就是C中有次品；次品可以是重，也可以是轻。
2. 左边倾斜。A > B, C中都是好球, 也就是A 或者 B中有次品，次品可以是重，也可以是轻。
3. 右边倾斜。A < B, C中都是好球, 也就是A 或者 B中有次品，次品可以是重，也可以是轻。

假如每次称重都是区分3中状态，3次称重可以区分27种状态 3^3 = 27。 因为有24种状态，所以理论上可以称3次找出次品。如果是14个球，状态就有28种，称3次就无论如何都找不出来了。

定义称几次为K，球的个数为N，理论中可以有解的公式如下, 3的K次方 大于等于 2N

3 ^ K >= 2N

3. 解题步骤

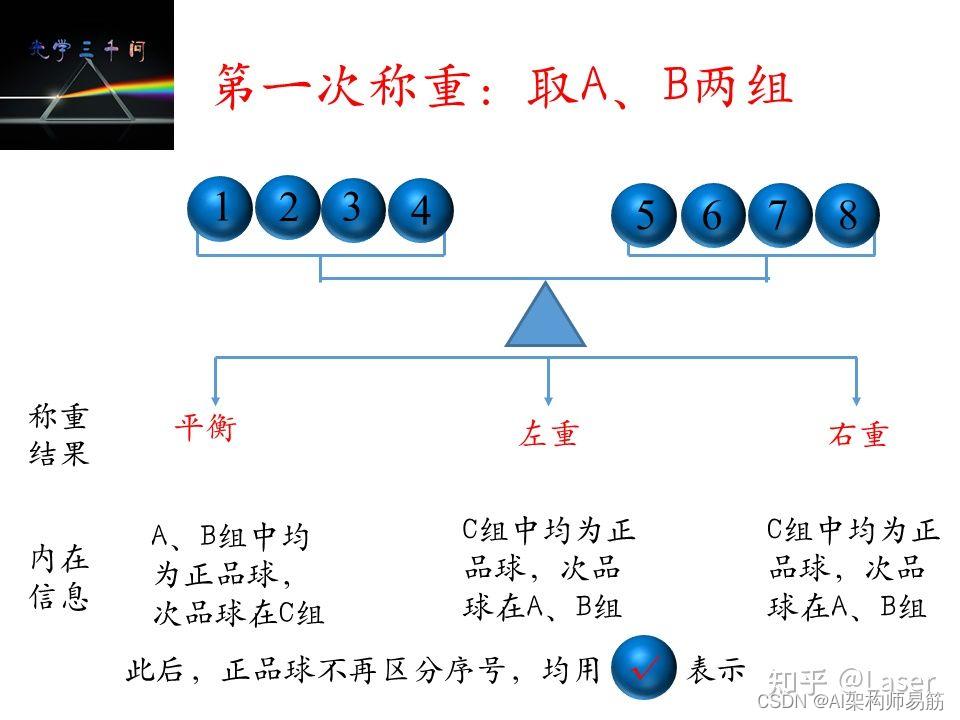
第一次称重可能会有三种不同的结果，我们根据不同的结果再进行后两次称重。

首先，考虑第一种平衡的结果，下一步我们从A组中取出三个正品球与C组中9、10、11号球称重。

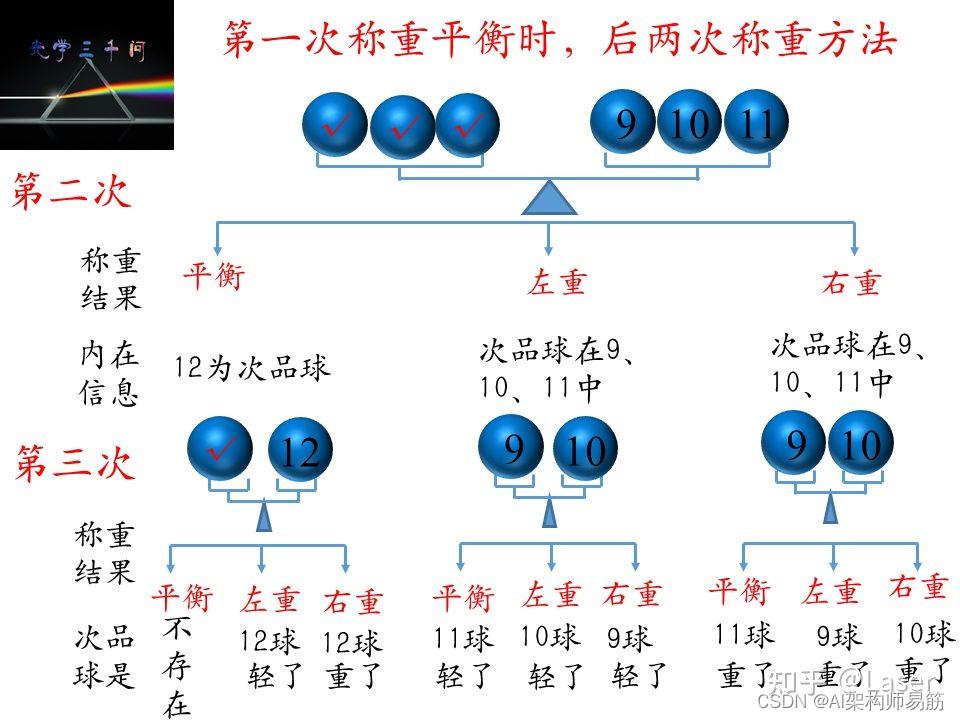
考虑第二种左重的结果，下一步我们从C组中取出三个正品球替换A组中2、3、4号球，然后将2、3、4号球替换6、7、8号球。

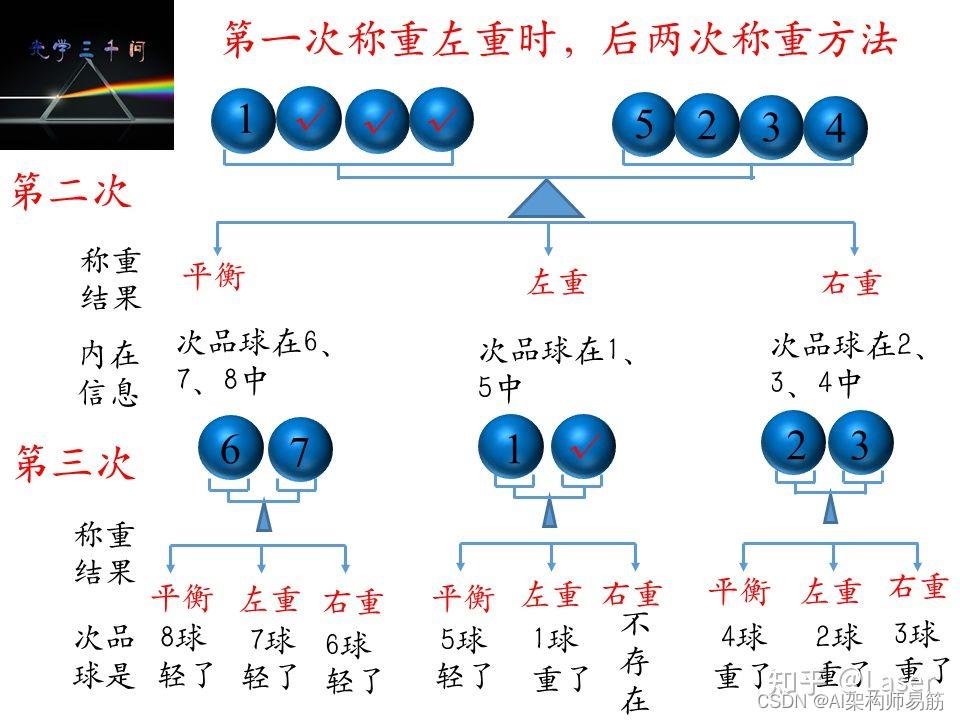
同理，考虑第三种右重的结果，下一步我们从C组中取出三个正品球替换A组中2、3、4号球，然后将2、3、4号球替换6、7、8号球。

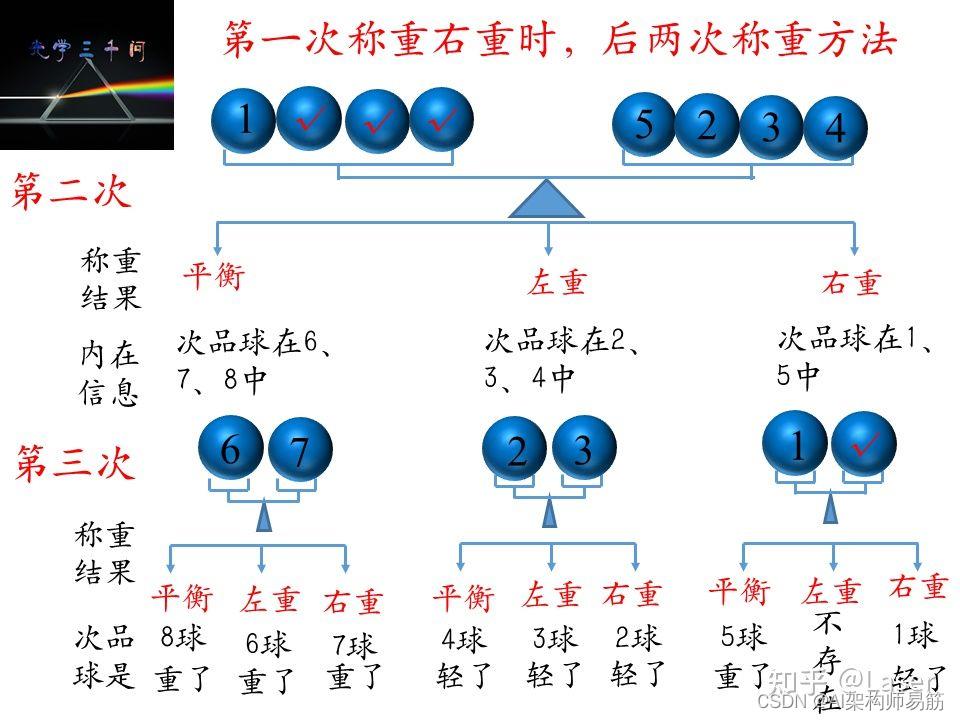
参考

https://zhuanlan.zhihu.com/p/386160442
《计算之魂》-- 吴军