虽然简单但确不能不会的推荐算法重点回顾

Posted 2022-08-01 搜索与推荐Wiki

本文为《推荐系统与深度学习》第四章的复习笔记，只记录了一些要点，希望能够快速的进行复习，如果发现哪一个点不明白的话，可以自行展开学习。

4.1 基于内容的推荐算法

基于内容的推荐算法步骤：

• 特征（内容）提取
• 用户偏好计算
• 内容召回（召回用户偏好的top K）
• 物品排序（可以根据top K中其他用户打分平均值最高的top N推荐给用户，好处是可以考虑其他用户的意见）

优点：

• 物品没有冷启动问题（因为物品的内容特征不依赖于用户数据），推荐出的物品也不会存在过于热门的问题
• 能够捕获到用户的特殊偏好
• 原理简单，方便问题定位

基于内容推荐的特征提取

• 结构特征（可以做onehot编码）
• 非结构化特征（eg，文章内容，可以进行分词，得到一个词库T）
  • 基础统计法（存在则对应位置为1，不存在对应位置为0）
  • 词频统计法（对应位置为归一化后的TF-IDF值）

缺点：

• 要求内容能够抽取出有意义的特征，且要求这些特征内容有良好的结构性
• 推荐精度较低，相同内容特征的物品差异性不大

TF-IDF的归一化公式：
$$w_{k,j}=\frac{TF-IDF(t_k,d_j)}{\sqrt{{\sum }_{s=1}^{T}TF-IDF(t_k,d_j{)}^2}}$$

上述公式保证整个文档的tf-idf和为1，参考：https://www.cnblogs.com/helloandhey/p/11880915.html

4.2 基于协同的推荐算法

基于近邻的推荐算法分为：

• 基于用户的协同：给用户推荐相似用户喜欢的物品
• 基于物品的协同：

两者的异同：

• 从推荐场景考虑
  • 如果用户数远大于物品数，可以考虑使用ItemCF
  • UserCF适用于内容更新频率非常高的平台
  • UserCF适合于社交推荐，ItemCF适用于非社交
  • UserCF注重社会化，ItemCF注重个性化
• 从系统多样性
  • ItemCF推荐的多样性优于UserCF
  • ItemCF容易发现长尾物品，这样精度就会小于UserCF
• 从用户特点对推荐算法的影响：
  • UserCF假设用户会喜欢和他有相同喜好的用户喜欢的东西，但如果用户找不到兴趣相投的用户，效果就会大打折扣，因此用户是否适应UserCF算法跟他有多少近邻用户是成正比关系的
  • ItemCF假设用户喜欢和他以前喜欢物品的相似物品，如果一个用户喜欢物品的自相似度大，则说明他喜欢物品比较相似，即比较符合ItemCF的假设

4.3 基于矩阵分解的推荐方法

矩阵分解的方法有：

• SVD
• FM（隐语义模型）

基于奇异值分解的推荐算法流程：

• 加载用户对物品的评分矩阵
• 矩阵分解，求奇异值，根据奇异值的能量占比确定降维至k的数值
• 使用矩阵分解对物品评分矩阵进行降维
• 使用降维后的物品评分矩阵计算物品相似度，对用户未评分过的物品进行预测
• 产生前n个评分值高的物品，返回物品编号以及预测评分值

SVD缺点：

• 只通过一次分解来对原矩阵进行逼近，特征挖掘的层次不够深入
• 矩阵分解也没有运用到物品本身的内容特征

4.4 基于稀疏自编码的推荐算法

基础的自编码结构

• （1）简单的为三层的神经网络（输入层、隐藏层、输出层），输入为样本$x$的特征向量，让输出层的结果和输入层的相同，隐藏层的神经元设置为$k$个，即迫使自编码神经网络去学习输入数据的压缩表示，同时也必须从$k$维的隐藏神经元激活度向量中重构出样本特征维度数目的输入值。
• （2）如果网络的输入数据是完全随机的，比如每个输入都是一个跟其他特征完全无关的独立同分布高斯随机变，那么这一压缩表示将会非常难学习，但是如果输入数据中隐含着一些特定的结构，比如某些输入特征是彼此相关的，那么这一算法就可以发现输入数据中的这些相关性。
• （3）有时为了能更有效地找出隐含在输入数据内部的结构和模式，会寻找一组超完备基向量，其维度可能比输入的特征维度还要高
• （4）在（3）中，隐藏神经元的数量比较大，可以给自编码神经网络增加一些限制，使得满足稀疏性的要求。比如如果神经元输出接近于1时，认为被激活，接近于0时认为被抑制，即Dropout，使得神经元大部分时间都被抑制的被称为稀疏性限制。

多层结构

自编码是一种最基础的结构，可以进一步利用深度学习的思想，学习到高层抽象特征，比如：栈式自编码。

栈式自编码原理

采用贪婪训练法进行训练，即通过三层的自编码结构得到隐藏层的特征表示$h^1$，然后将$h^1$作为第二个稀疏自编码的输入，得到二阶的特征表示$h^2$

然后将二阶的特征表示$h^2$输入到一个$softmax$分类器，训练得到一个将二阶特征表示映射到数字标签的模型。

然后将上述的三个网格结构结合起来构建一个包含：输入层-> 隐藏层 -> 隐藏层->$softmax$分类器层 的完整的栈式自编码结构。

稀疏自编码在推荐系统中的应用

背景：输入层为一首歌曲，向量特征为歌曲被用户收藏的数据，输出层为音乐的流派分类结果。希望训练出歌曲的特征向量，用于歌曲的相似度计算。

数据：

• 输入层，每首歌曲的输入向量$u_1,u_2,...,u_n$，其中$u_i$表示是否被用户收藏过，收藏过为1，未收藏过为0。输入矩阵为$(m+1)\ast n$（包含一个截距项），$m$为用户数量，$n$为歌曲数量
• 隐藏层，$(k+1)\ast n$，$k+1$表示特征维度数
• 输出层，音乐的流派分类结果

隐藏层到输出层的权重连接，一般的神经网络中会进行忽略，但是在自编码网络中，连接层是有意义的。这些权重作用是将歌曲特征向量映射到用户是否听过/喜欢该歌曲，其实就是用户的低维特征

通过上述的自编码学习，把第二个隐藏层的$h^2$取出来，即歌曲以流派分类为目标降维压缩后的向量。

该向量不仅使用到了用户的群体收藏行为，也运用了歌曲的流派特征信息，可以表示歌曲更多的特征信息。

紧接着就可以利用这些向量计算音乐的相似度，然后将用户未收藏的音乐推荐给用户，注意前后行为的一致性。

4.5 基于社交网络的推荐算法

社交网络结构：

• 社交图谱（相互认识，在网络中可以使用无向图表示）
• 兴趣图谱（单向关注，在网络中可以使用有向图表示）
• 标签图谱（共同关注某个标签，兴趣相似，但没有建立真正的社交关系）

好友相似度计算：

1、基于共同关注好友的比例计算好友的相似度：
$$w_{u,v}=\frac{|out(u)\bigcap out(v)|}{\sqrt{|out(u)|.|out(v)|}}$$
其中：

• $out(u)$ 表示 用户 $u$有关注的好友列表
• $out(v)$ 表示 用户 $v$有关注的好友列表

适合计算普通用户之间的相似度

Python 效率低，可以使用spark 的 Graphx进行计算

2、基于共同被关注的用户比例计算好友的相似度
$$w_{u,v}=\frac{|in(u)\bigcap in(v)|}{\sqrt{|in(u)|.|in(v)|}}$$
其中：

• $in(u)$ 表示关注用户$u$的好友列表
• $in(u)$ 表示关注用户$v$的好友列表

适合计算大V之间的相似度

3、用户 $u$关注的用户中，有多大比例也关注了用户$v$

$$w_{u,v}=\frac{|out(u)\bigcap in(v)|}{\sqrt{|out(u)|.|in(v)|}}$$

node2vec

node2vec论文：《node2vec：Scalable Feature Learning for Networks》

network embedding就是一种图特征的表示学习方法，它从输入的网络图中，学习到节点的表达。

node2vec的整体思路分为两个步骤：

• random walk（随机游走），即通过一定的规则抽取一些点的序列
• 将点的序列输入至word2vec模型从而得到每个节点的embedding向量

random walk

随机游走的基本流程，给定一张图$G$和一个起始节点$S$，标记起始节点位置为当前位置，随机选择当前位置节点的一个邻居并将当前位置移动至被选择的邻居位置，重复以上步骤$n$次，最终会得到初始节点到结束节点的一条长度为$n$的“点序列”，此条“点序列”即称为在图$G$上的一次random walk。

从描述中可以看出random walk 算法可以分为两步：

• （1）选择起始节点
• （2）选择下一跳节点

起始节点选择有两种方法：

• 按照一定规则随机从图中抽取一定数量的节点
• 以图中所有节点作为起始节点（倾向于使用这种）

选择下一跳节点最简单的方法是按照边的权重随机选择， 但是在实际应用中，希望能控制广度优先还是深度优先，从而影响random walk能够游走的范围。

一般来说深度优先便利，发现能力更强，广度优先的方法，社区内的接待你更容易出现在一个路径里。

斯坦福大学计算机教授 Jure Leskovec给出了一种可以控制广度优先或者深度优先的方法。

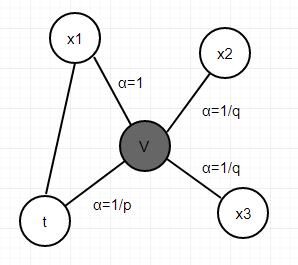
以上图为例，我们假设第一步是从 $t$随机游走到 $v$，接下来要确定下一步的邻接节点。参数 $p$ 和 $q$ 用以调整游走节点的倾向。

• $p$：计算回到上一节点的概率；
• $q$：计算走到远离上一节点的节点概率。

首先计算当前节点的邻居节点与上一节点 $t$ 的距离 $d$，根据公式可得 $\alpha$

1 / p , d = 0