jdk（Windows/Mac含M1/M2 Arm原生JDK）安装，附各个版本JDK下载链接

Posted 2023-04-04 Elastic开源社区

文章目录

• 安装建议及注意事项
• 1、JDK下载
• • 1.1 官方下载
  • 1.2 JDK 国内镜像
  • 1.3 Azul JDK（支持ARM原生：苹果M1、M2系列）
• 2、Widows系统安装及配置
• • 2.1 安装
  • 2.2 配置环境变量
  • • 2.2.1 打开系统设置
    • 2.2.2 打开环境变量设置项
    • 2.2.3 配置环境变量参数值
    • 2.2.4 把`JAVA_HOME`添加到`Path`中
  • 2.3 验证
• 3、Mac系统安装指南
• • 3.1 安装
  • 3.2 配置环境变量
  • • 3.2.1 首先确认 JDK 的安装路径
    • 3.2.2 配置`bash_profile`
    • 3.2.3 配置`JAVA_HOME`变量
    • 3.2.4 保存配置
  • 3.3 刷新`.bash_profile`文件
  • 3.4 验证

安装建议及注意事项

• 他发任他发，我用Java 8，并不是没有道理，版本未必越新越好，结合自己的环境综合考虑
• 本文会给出不同系统和版本的jdk下载地址和安装步骤，根据自己的需要直接跳转至文章对应小节即可。
• 本文分别会给出不同系统及不同场景下的安装建议。如有其他问题，可在文末留言。

1、JDK下载

1.1 官方下载

选择对应的操作系统及JDK版本，点击直达官方下载链接

	Windows	Mac	Linux
Java 8	JDK 8 For Win	JDK 8 For Mac	JDK 8 For Linux
Java 11	JDK 11 For Win	JDK 11 For Mac	JDK 11 For Linux
Java 17	JDK 17 For Win	JDK 17 For Mac	JDK 17 For Linux
Java 18	JDK 18 For Win	JDK 18 For Mac	JDK 18 For Linux
Java 19	JDK 18 For Win	JDK 18 For Mac	JDK 18 For Linux

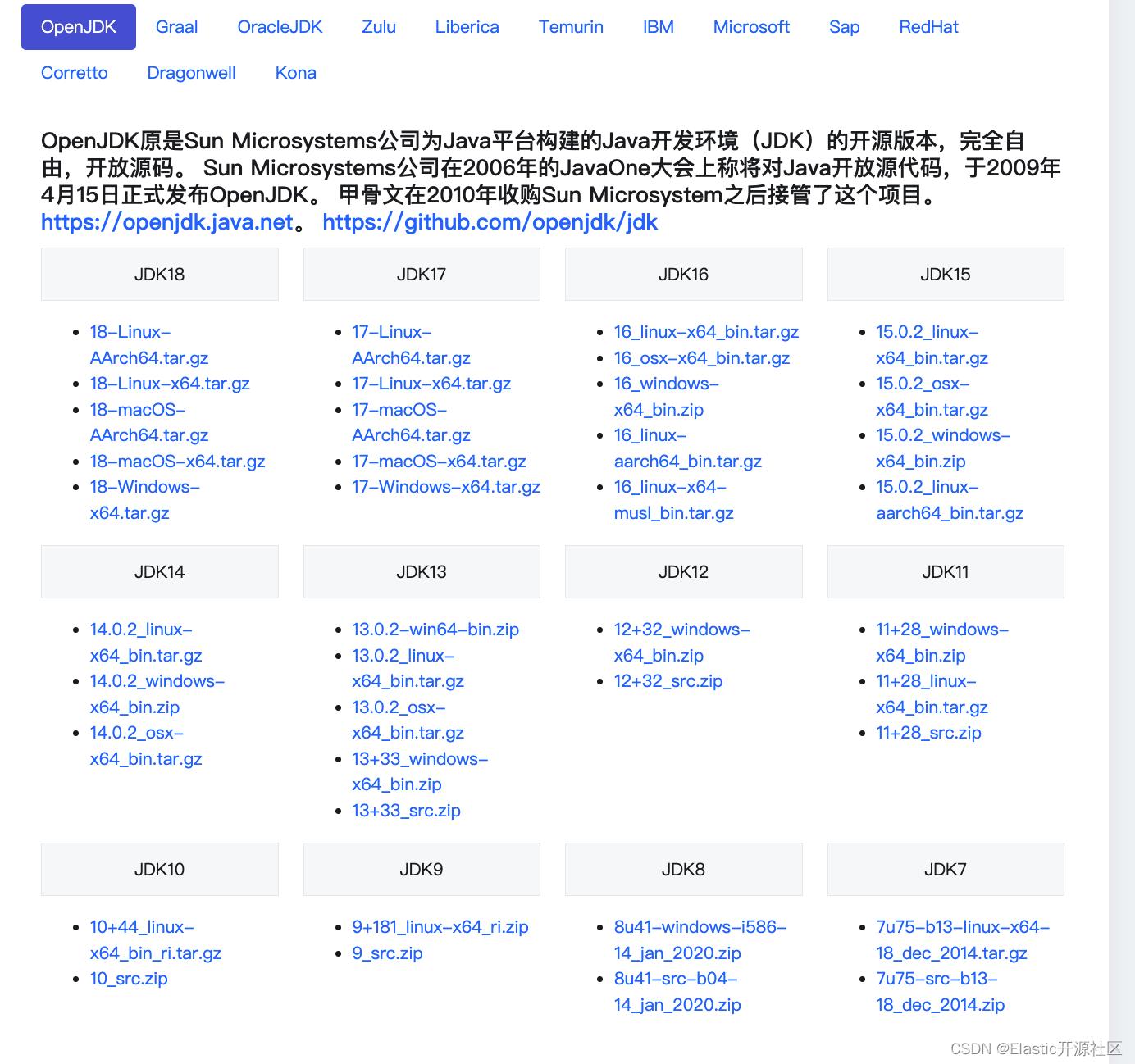
1.2 JDK 国内镜像

• 下载：https://www.injdk.cn/

• 特点：几乎囊括了各个渠道的所有受支持的 JDK 版本，非常方便，建议收藏！

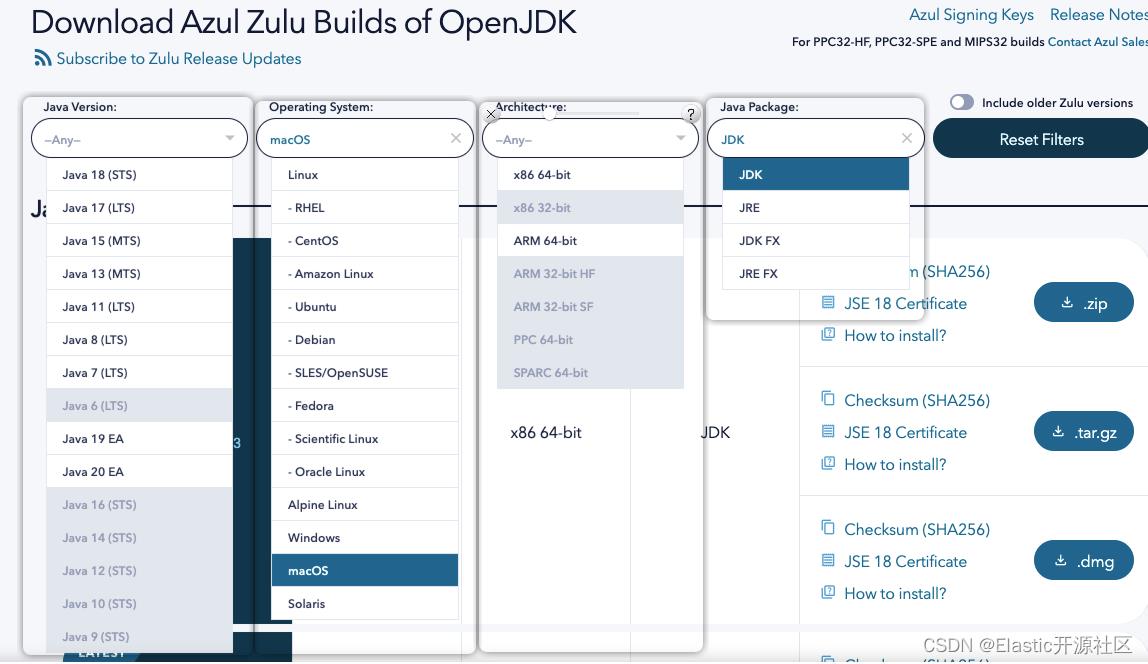
1.3 Azul JDK（支持ARM原生：苹果M1、M2系列）

• 地址：https://www.azul.com/downloads/

• 特点：版本齐全，兼容的系统版本多，原生支持 ARM 架构，兼容苹果 M1、M2 系列Mac

2、Widows系统安装及配置

2.1 安装

安装没有过多可交代的，一直点下一步即可

唯一需要注意的就是，如果你没有修改安装路径，要记得jdk安装的位置。安装本身没有难度，就不再多说了，安装完毕之后点击关闭即可。

2.2 配置环境变量

2.2.1 打开系统设置

Win + E 打开计算机，右键属性（或者右键左下角win图标，点击设置）进入系统设置菜单

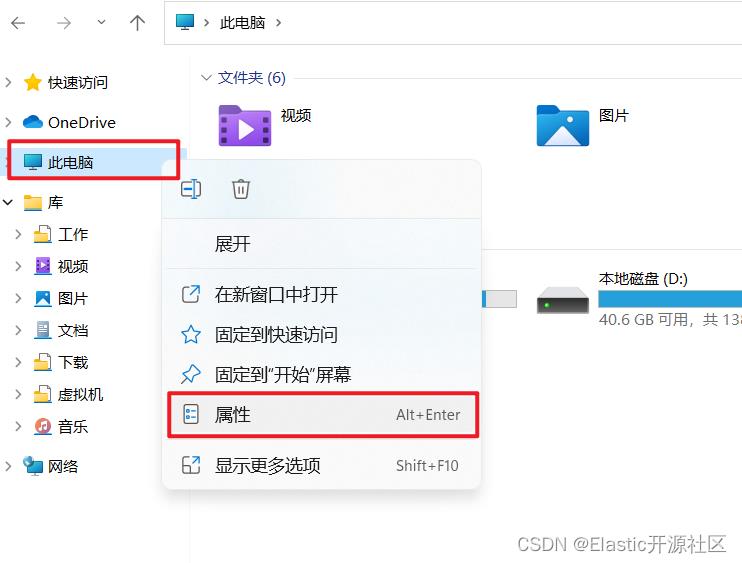
对于部分Win10和Win11用户以下操作和上面操作效果相同

2.2.2 打开环境变量设置项

点击属性之后，在弹出窗口中选择环境变量，如果没有弹出系统属性窗口，而是设置界面，参考下一步。

对于Win10和Win 11用户，如果点击属性之后没有直接弹出系统属性菜单，可以在系统设置左上方搜索框中直接搜索环境变量，直接选择或者按回车选择编辑系统环境变量或者编辑账号环境变量均可，我这里选择的前者。

2.2.3 配置环境变量参数值

在系统变量下点击新建

弹出窗口中，变量名填写JAVA_HOME，注意需要全部大写。
参数值填写刚才安装JDK时的安装路径，注意是根目录，不是bin目录

2.2.4 把JAVA_HOME添加到Path中

在系统变量中，找到变量名称为Path的变量，如果没有，则点击创建。

在弹窗的环境变量编辑窗口中，点击新建，输入%JAVA_HOME%\\bin，点击保存。

2.3 验证

3、Mac系统安装指南

jdk下载方式见本文第一部分，不过多赘述，选择合适版本即可。

3.1 安装

下载dmg文件，我这里以jdk-8u341-macosx-x64版本为例，点击继续

输入密码，点击安装

3.2 配置环境变量

3.2.1 首先确认 JDK 的安装路径

默认情况下，JDK的安装路径为：

/Library/Java/JavaVirtualMachines/

博主这里安装了3个版本的jdk，如图所示：

3.2.2 配置bash_profile

方式一：图形界面操作

在家目录下，打开.bash_profile文件，默认情况下，.bash_profile文件时隐藏的，可以用shift + command + .快捷键切换打开/关闭显示隐藏文件。注意快捷键中包含一个.!，如果是黑苹果系统，使用shift + win + .

如果不知道家目录是哪个或者在哪里，直接打开终端（可使用快捷键command + 空格，然后输入终端）

然后在终端中输入open ~ 即可

open ~

方式二：终端操作（推荐）
使用vi或者vim编辑器直接点开文件，输入vim ~/.bash_profile

vim ~/.bash_profile

如果权限不足，可以加sudo执行，输入密码即可。

sudo vim ~/.bash_profile

3.2.3 配置JAVA_HOME变量

打开.bash_profile之后，在文件末尾（或任意位置）添加以下内容：

JAVA_HOME=/Library/Java/JavaVirtualMachines/jdk1.8.0_311.jdk/Contents/Home
PATH=$JAVA_HOME/bin/:.
CLASSPATH=$JAVA_HOME/lib/tools.jar:$JAVA_HOME/lib/dt.jar:.
export JAVA_HOME
export PATH
export CLASSPATH

注意:

• JAVA_HOME变量其中的jdk1.8.0_311.jdk是你的 JDK 的目录名称，替换成你电脑中安装的目录名称即可。

• 注意PATH=$JAVA_HOME/bin/:.最后有一个.

• 如果你还有其他的变量，可以在PATH后的冒号后面追加即可，比如，假设我还有一个M2_Home的变量，就可以按照如下配置：

  JAVA_HOME=/Library/Java/JavaVirtualMachines/jdk1.8.0_311.jdk/Contents/Home
  PATH=$JAVA_HOME/bin/:$M2_Home/bin/:$PATH:.
  CLASSPATH=$JAVA_HOME/lib/tools.jar:$JAVA_HOME/lib/dt.jar:.
  export JAVA_HOME
  export PATH
  export CLASSPATH
  export M2_Home=/Users/wulei/Services/apache-maven-3.6.3
  

• 如果目录中不包含.bash_profile，创建一个新文件即可！

3.2.4 保存配置

修改完毕后，保存文件，步骤如下：

• 切换至输入法至英文输入状态
• 按ESC进入底行模式（命令模式）
• 输入wq回车确认保存并推出

3.3 刷新.bash_profile文件

配置完毕后，需要执行source ~/.bash_profile使其生效

source ~/.bash_profile

3.4 验证

打开终端，输入java -version，当输出 java 版本号的时候，即表示环境变量已配置成功

kummer定理

没有校验过， 可能有锅qwq

---

Kummer定理
设(n、m)为正整数，(p)为素数，则(C_{n+m}^m)含(p)的幂次数等于(m+n)在p进制下的进位次数（在加法过程中）。

---

前置芝士：
(n!)含有的(p)的幂次数为：

[sum_1^{infty} Big[ frac{n}{p^i} Big] ]

(这个随便画画就可以证明了)

---

证：
(C_{n+m}^m)含(p)的幂次数为:

[sum_1^{infty} Big[ frac{m+n}{p^i} Big] - sum_1^{infty} Big[ frac{n}{p^i} Big] - sum_1^{infty} Big[ frac{m}{p^i} Big] ]

[=sum_1^{infty} ( Big[ frac{m+n}{p^i} Big] - Big[ frac{n}{p^i} Big] - Big[ frac{m}{p^i} Big] ) ]

接下来只要算出(m+n)在p进制下的进位次数（在加法过程中）就好。
将(m+n、n、m)分别写成(p)进制(下标为0的是最低位):

[overline{c_0c_1c_2 cdots c_{unknown}} 、overline{n_0n_1n_2 cdots n_{unknown}} 、overline{m_0m_1m_2 cdots m_{unknown}} ]

在加法过程中， 定义第(pos)位发生进位这个事件发生的条件为

[n_{pos}+m_{pos} geq p ]

若第(pos)位发生了进位， 则

[overline{n_{pos+1} cdots n_{unknown}} +overline{m_{pos+1} cdots m_{unknown}} < overline{c_{pos+1} cdots c_{unknown}} ]

当然， 由于进位最多进一((lfloor frac{(p-1)+(p-1)}{p} floor = 1))， 故当第(pos)位发生进位时

[overline{c_{pos+1} cdots c_{unknown}} - overline{n_{pos+1} cdots n_{unknown}} - overline{m_{pos+1} cdots m_{unknown}} = 1 ]

反之

[overline{n_{pos+1} cdots n_{unknown}} +overline{m_{pos+1} cdots m_{unknown}} = overline{c_{pos+1} cdots c_{unknown}} ]

即

[overline{c_{pos+1} cdots c_{unknown}} - overline{n_{pos+1} cdots n_{unknown}} - overline{m_{pos+1} cdots m_{unknown}} = 0 ]

然后在(p)进制下(m+n)过程中的进位次数用数学式子表示就是这个
((overline{x_{pos+1} cdots x_{unknown}}) = (x/p^{pos+1}))

[sum_1^{infty} ( Big[ frac{m+n}{p^i} Big] - Big[ frac{n}{p^i} Big] - Big[ frac{m}{p^i} Big] ) ]

然后就证毕了。