Cocos2d-x 3D渲染技术

Posted 2023-04-04 浮生述梦

3D坐标系统

五个空间

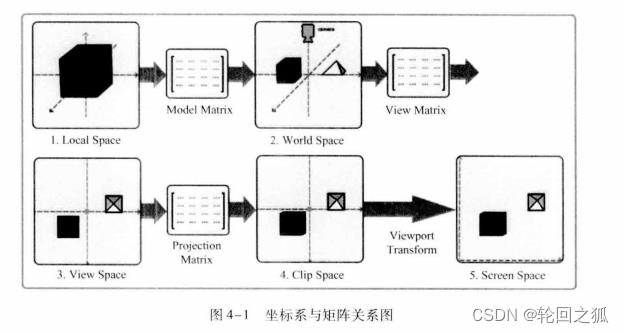
要把游戏模型显示到屏幕需要经历五个空间。

1. 局部空间 （Local Space，模型空间）
2. 世界空间 （Wolrd Space，游戏空间）
3. 观察空间 （View Space，视觉空间）
4. 裁剪空间 （Clip Space）
5. 屏幕空间 （Screen Space）

局部空间 （Local Space）

指模型对象所在的坐标空间，即建模软件的空间。

一般在导出创建的模型时，将模型的的坐标设为（0，0，0），目的是为了保持和世界坐标重合，方便调整其在世界坐标中的位置。

世界空间 （Wolrd Space）

游戏所在的场景就是世界空间。

将模型放到世界空间之后，可以对模型对象进行平移，缩放，旋转等操作，本质上就是通过矩阵的转换算法实现的。（模型举证）

观察空间 （View Space）

通过虚拟摄像机观察世界空间。

在游戏中，可以操作视角看到周围的物体。本质就是操作虚拟摄像机，将视线内的物体转换到摄像机的坐标系中。

观察空间也就是摄像机所观察的空间，是将物体对象的世界空间坐标转换为观察视觉内的坐标。

观察空间的计算需要使用观察矩阵

裁剪空间（Clip Space）

不能将所有的物体都移动到观察空间中，没有在视线范围内的物体需要被裁剪掉。

平截头体：由投影矩阵创建的观察区域。出现在其区域内的物体都会出现在屏幕中。

将场景中的物体从观察空间转换到裁剪空间，需要定义投影矩阵。

将一定范围内的坐标转化到标准设备坐标系的过程叫投影。

两种投影矩阵：

1. 正交投影矩阵 ======> 正交投影
2. 透视投影矩阵 ======> 透视投影

正交投影

正交投影矩阵定义了一个类似立方体的平截头体。在立方体外的物体都会被裁剪掉。

在创建一个正交投影矩阵的时候，需要指定平截头体的宽度、高度和长度的远近。

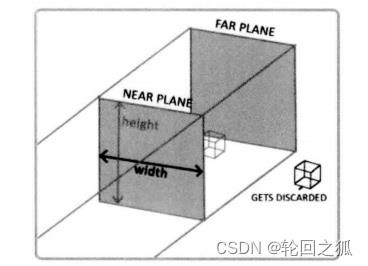
摄像机的可视坐标系由这个平截头体的宽、高、深来决定。

由此可以看到，正交投影的矩阵由宽和高来决定，和深度无关。即不管远近，所显示的部分和近裁剪面是一致的。

作用：由于正交投影没有远近之分，一般作用于UI的摄像机上。

bool Camera::initOrthographic(float zoomX, float zoomY, float nearPlane, float farPlane)

    _zoom[0] = zoomX;
    _zoom[1] = zoomY;
    _nearPlane = nearPlane;
    _farPlane = farPlane;
    Mat4::createOrthographicOffCenter(0, _zoom[0], 0, _zoom[1], _nearPlane, _farPlane, &_projection);
    _viewProjectionDirty = true;
    _frustumDirty = true;
    _type = Type::ORTHOGRAPHIC;
    
    return true;

zoomX ： 平截头体的宽

zoomY ： 平截头体的高

nearPlane ：近裁剪面

farPlane ： 远裁剪面

然后调用函数createOrthographicOffCenter

void Mat4::createOrthographicOffCenter(float left, float right, float bottom, float top,
                                         float zNearPlane, float zFarPlane, Mat4* dst)

    GP_ASSERT(dst);
    GP_ASSERT(right != left);
    GP_ASSERT(top != bottom);
    GP_ASSERT(zFarPlane != zNearPlane);

    memset(dst, 0, MATRIX_SIZE);
    dst->m[0] = 2 / (right - left);
    dst->m[5] = 2 / (top - bottom);
    dst->m[10] = 2 / (zNearPlane - zFarPlane);

    dst->m[12] = (left + right) / (left - right);
    dst->m[13] = (top + bottom) / (bottom - top);
    dst->m[14] = (zNearPlane + zFarPlane) / (zNearPlane - zFarPlane);
    dst->m[15] = 1;

正交投影的平截头体为一个长方体[left,right][bottom,top][far,near]

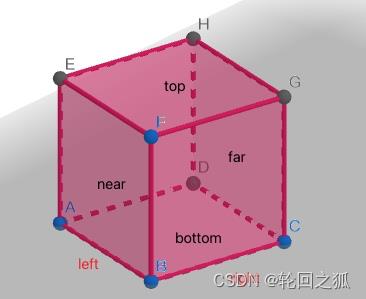
那么需要把这个长方体转换到[-1,1][-1,1][-1,1]中

那么就需要两步。

平移

算出上面的长方体的中心点。

``[(left+right) / 2,(bottom+top) / 2,(far+near) / 2] ``

那么将这个点移动到原点。

平移公式为：

$$\left|\begin{array}{cccc}1& 0& 0& T_x\\ 0& 1& 0& T_y\\ 0& 0& 1& T_z\\ 0& 0& 0& 1\end{array}\right|\cdot \left\{\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right\}=\left\{\begin{array}{c}{x}_1\\ y_1\\ z_1\\ 1\end{array}\right\}$$

其中 x1,y1,z1为新移动的点。

那么就可以得到，平移矩阵为

$$T^{-1}(t)=T(-t)=\left|\begin{array}{cccc}1& 0& 0& -T_x\\ 0& 1& 0& -T_y\\ 0& 0& 1& -T_z\\ 0& 0& 0& 1\end{array}\right|$$

所以，该长方体的平移矩阵为：

$$M_{translate}=\left|\begin{array}{cccc}1& 0& 0& -\frac{left+right}{2}\\ 0& 1& 0& -\frac{bottom+top}{2}\\ 0& 0& 1& -\frac{far+near}{2}\\ 0& 0& 0& 1\end{array}\right|$$

缩放

设缩放因子为s，则沿着坐标轴的缩放变换矩阵为：

S ( s ) = S ( s x , s y , s z ) = ∣ s x 0 0 0 0 s y

UE4 分层材质 Layerd Materials

 

在UE4中最正规的材质制作流程就像：

• 建立新材质，并将其调整为达至完美。

• 在内容浏览器中，建立新材质函数，并将所有材质函数节点复制/粘贴到其中。

• 将网络连接到新的 Make Material Attributes（建立材质属性）节点，并将其连接到“函数”（Function）输出。

• 保存该函数。

• 将该函数从内容浏览器拖放到材质编辑器中。现在，它变为材质层。

• 使用材质层混合函数将多个材质层混合到一起。　　

该流程的具体步骤：

1，新建材质，将材质调好

2，新建材质函数，复制该材质，将材质函数暴露到函数库，使用MakeMaterialAttribute即可创建跟材质的最终输出一样的节点，在材质中勾选use material attribute就能让材质的输出节点合成一个Material Attributes

3，在最终的材质中引入各个材质层即各个调好的材质函数，通过MatLayerBlend_Standard等节点进行混合。

材质层混合：

　　

 

 

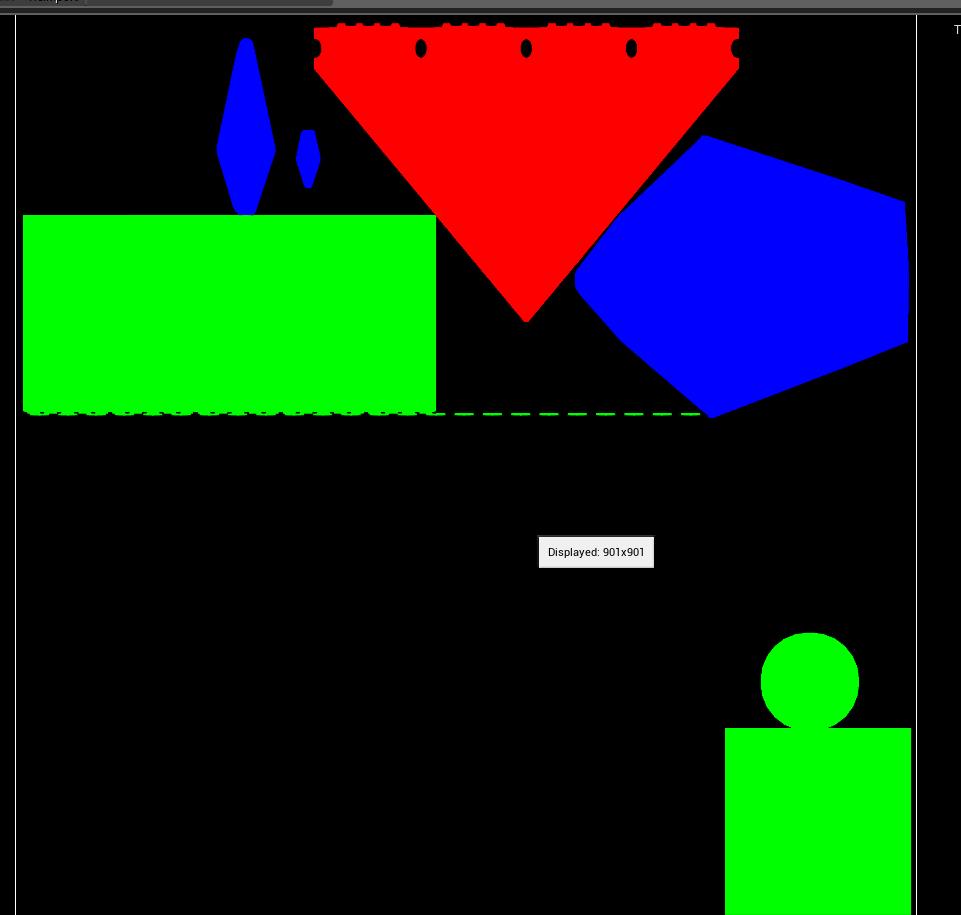
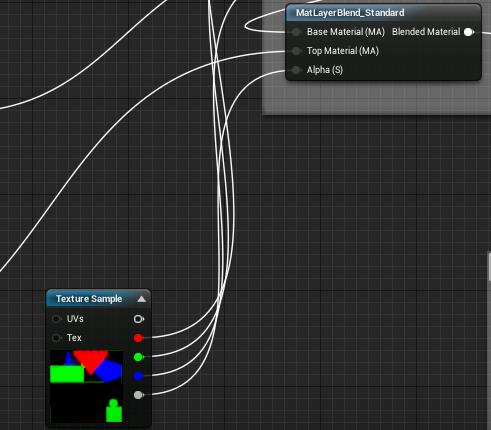
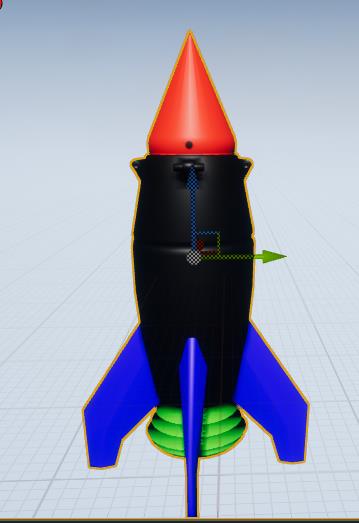
制作类似这种图片，通过各通道的值当做混合函数的alpha值来决定模型的每个部位使用哪个材质层。

使用材质层的优缺点：

　　简化最终材质，看起来没那么乱，便于修改，需要修改哪部分材质只需要到对应材质函数修改，做好的材质层可以复用，

　　虽然分层材质非常适合于处理多材质设置，但使用这些材质时务必小心谨慎。它们可能会对性能产生严重影响，简而言之，如果您 可以 应用多个材质来代替使用分层材质，请这样做。如果您 必须 对材质的放置位置进行逐个像素的控制，请使用分层材质。