动态规划简介

Posted 2023-04-03 成、谋

动态规划（Dynamic Programming）是一种常见的算法思想，它广泛应用于各种领域中的优化问题，如图像处理、自然语言处理、生物信息学等。动态规划让计算机快速求解具有重叠子问题和最优子结构性质的复杂问题，它一直是算法竞赛中最受欢迎的话题之一。

一、什么是动态规划？

动态规划是一种利用历史记录来避免重复计算的算法。它将复杂的问题分解成小问题，并保存每个子问题的解以供后续使用。在解决子问题的过程中，动态规划通常会建立一张表格来记录不同状态下的解决方案，并逐步推导出最终的解决方案。

二、动态规划算法流程

2.1 一般的流程

1、定义子问题

动态规划算法的第一步是将原问题划分为若干个规模更小、相对独立的子问题，可以用数组或矩阵来表示。

2、状态转移方程

接下来，我们需要推导出这些子问题之间的状态转移方程，即如何通过已经求解的子问题得到当前问题的解。

3、处理边界条件

对于任何算法，都需要对边界条件进行特殊处理，以避免出现溢出或无限递归等问题。在动态规划中，边界条件就是最小子问题，可以从中直接得到答案。

4、记录和利用历史结果

将子问题的答案保存在数组或矩阵中，可以节省重复计算的时间，从而更加高效。

5、返回结果

最终，我们可以将得到的结果返回给主调用程序。

2.2 需要重点注意的三个问题

这三个点参考自 告别动态规划，连刷40道动规算法题，我总结了动规的套路_Hollis Chuang的博客-CSDN博客

1. 定义数组元素的含义，在上面的流程中可以看到，我们会用一个数组，来保存历史数组，假设用一维数组 dp[] 。这时有一个非常重要的点，就是规定这个数组元素的含义，如这个 dp[i] 是代表什么意思？

2. 找出数组元素之间的关系式，这个类似于中学的归纳法，当我们要计算 dp[n] 时，可以利用 dp[n-1]，dp[n-2]…..dp[1]，来推出 dp[n] ，也就是可以利用历史数据来推出新的元素值，所以我们要找出数组元素之间的关系式，例如 dp[n] = dp[n-1] + dp[n-2]

3. 找出初始值。这是我们归纳的基础！！！例如 dp[n] = dp[n-1] + dp[n-2]，我们一直往前推导，直到dp[2],dp[1]，这时我们发现dp[2],dp[1]不能再分解了，这两个的值需要我们直接给出！

三、动态规划例题分析

下面以一个简单的例题来进行动态规划算法的分析：

假设一个人要跨越一个长方形网格（m*n），从左上角到右下角，只能 向下或向右走，每次只能移动一格。问有多少种不同的走法？

我们甚至可以不用枚举每个方格的路径，而是借助动态规划的思想，来推导出总的走法数。

我们可以用f（i,j）表示从（1,1）走到（i,j）的方案总数，经过分析，可得出状态转移方程：

f(i,j) = f(i-1,j) + f(i,j-1)（i,j不在边缘，即i!=1,j!=1)
f(i,1) = 1（j==1,i!=1)
f(1,j) = 1（i==1,j!=1)

我们使用一个二维数组dp[i][j]来记录每个状态f(i,j)的解，最终，只需要返回dp[m][n]的值即可。

代码实现如下：

int uniquePaths(int m, int n)  
    if (m <= 0 || n <= 0) 
        return 0; 
    vector<vector<int>> dp(m, vector<int>(n, 0)); 
    for (int i = 0; i < m; ++i)  
        dp[i][0] = 1; 
     
    for (int j = 0; j < n; ++j)  
        dp[0][j] = 1; 
     
    for (int i = 1; i < m; ++i)  
        for (int j = 1; j < n; ++j)  
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; 
         
     
    return dp[m - 1][n - 1]; 

以上就是动态规划算法的一般思路和过程。当然，动态规划并不是解决所有问题的最优解法，有些问题还需要其他算法进行优化处理。但可以肯定的是，动态规划算法的思想和方法，是我们需要了解和学习的重要算法之一。

四、附加一个练习题

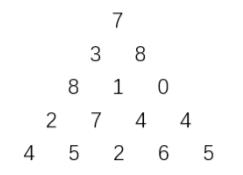
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。

路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个数。此外，向左下走的次数与向右下走的次数相差不能超过 1。

题目链接： 数字三角形 - 蓝桥云课 (lanqiao.cn)

输入描述

输入的第一行包含一个整数 N (1≤N≤100)，表示三角形的行数。

下面的 N行给出数字三角形。数字三角形上的数都是 0 至 100 之间的整数。

输出描述

输出一个整数，表示答案。

测试样例

输入样例

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

输出样例

27

我的代码

#include <bits/stdc++.h>
using namespace std;
int main()

  // 请在此输入您的代码
  int n,dp[100][100],m;
  int a[100][100];
  cin>>n;
  for(int i=0;i<n;i++)
    for(int j=0;j<=i;j++)
      cin>>a[i][j];
    
  
  dp[0][0]=a[0][0];
  for(int i=1;i<n;i++)
    dp[i][0]=dp[i-1][0]+a[i][0];
  for(int i=1;i<n;i++)
    dp[i][i]=dp[i-1][i-1]+a[i][i];
  for(int i=2;i<n;i++)
    for(int j=1;j<i;j++)
      dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+a[i][j];
    
  
  if(n%2==0)
    m=max(dp[n-1][n/2],dp[n-1][n/2-1]);
  
  
  else m=dp[n-1][n/2];
  
  cout<<m;
  return 0;

分析：

首先输入数据，可以使用二维矩阵a[100][100]来存储数字三角形，如下图所示。

接下来，我们需要利用动态规划来求解最大累加和。

状态转移方程如下：

dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + a[i][j]

其中，dp[i][j]表示从顶部到(i,j)的最大累加和；a[i][j]表示数字三角形中(i,j)位置的值。

从上往下进行动态规划，最终把dp数组填充完，其中，最终结果应该是在dp数组的最后一行去找。

注意还没完！！！

向左下走的次数与向右下走的次数相差不能超过 1。这个条件我们还没有用到

通过找规律能够发现：如果n为奇数时，最后必然走到最后行最中间的数，如果为偶数，则取中间两个数的最大值。所以最终结果是在max(dp[n-1][n/2],dp[n-1][n/2-1])和dp[n-1][n/2]中取得。

动态规划与多阶段决策问题简介

文章目录

• 1.引例
• • 1.1最短路径问题
  • 1.2 库存成本最低问题
• 2、多阶段决策问题
• • 2.1 特点
  • 2.2 阶段和阶段变量
  • 2.3状态、状态变量、可能状态集
  • • 状态变量
    • 状态
  • 2.4决策、决策变量和允许变量集合
  • • 决策变量和允许决策集合
  • 2.5策略和允许策略集合
  • 2.6状态转移方程
  • 2.7指标函数
  • • 阶段指标函数
    • 过程指标函数
  • 2.8最优解
• 3. 数学模型

---

1.引例

1.1最短路径问题

动态规划求解从A到F的最短路径。

1.2 库存成本最低问题

某企业生产某种产品，每月月初按订货单发货，生产的产品随时入库，仓库最多能够储存产品90千件。在1至6月其生产成本和产品订单的需求数量情况如下表：

已知上一年底库存量为40千件，要求6月底库存量仍能够保持40千件。问：如何安排这6个月的生产量，使既能满足各月的定单需求，同时生产成本最低。

2、多阶段决策问题

2.1 特点

2.2 阶段和阶段变量

相互联系又有区别的子问题——阶段
描述阶段的变量——阶段变量（$k$表示）

2.3状态、状态变量、可能状态集

某特定时间与空间中位置及运动特征的量——状态
反映状态变化的量——状态变量
状态变量的取值范围或集合——可能状态集（可达状态集），可以是离散的也可以是连续的

状态变量

无后效性（马尔可夫性）——系统从某个阶段之后的发展，仅与当前状态及之后的决策决定，与之前的状态和经历无关——（强化学习应用）

状态

阶段$k$的初始状态$s_k$，终止状态$s_{k+1}$，可能状态集$S_k$，即$s_k\in S_k$。

2.4决策、决策变量和允许变量集合

从给定阶段的状态出发到下一个阶段状态的选择（行动$action$）——决策
描述决策变化的量——决策变量，可以是数、向量、其他量、也可是状态变量的函数
决策变量的取值范围——允许决策集合

决策变量和允许决策集合

记$u_k=u_k(s_k)$表示阶段$k$状态为$s_k$时的决策变量，允许决策集$U_k(s_k)$表示，允许决策集合实际是决策的约束条件

2.5策略和允许策略集合

决策序列——策略（全过程策略、$k$部字策略）
依次进行的$n$个决策构成的决策序列——全过程策略（简称策略），表示为
$$p_{1,n}{u}_1{u}_2,\cdots ,u_n$$
  从$k$阶段到第$n$阶段，依次进行的阶段决策构成的决策序列称为$k$部子策略，表示为$p_{k,n}{u}_k,u_{k+1},\cdots ,u_n$，显然，当$k=1$时的$k$部子策略就是全过程策略。
  不同策略的集合即允许策略集合，记作$P_{1,n}$。最有效果的策略称为最优策略

2.6状态转移方程

$$s_k+u_k(s_k)\Rightarrow s_{k+1}$$
  无后效性的转移过程：$s_{k+1}$只和$s_k$和$u_k(s_k)$有关，与之前的$s_1,s_2,\cdots ,s_{k-1}$及其决策$u_1(s_1),u_2(s_2),\cdots ,u_{k-1}(s_{k-1})$无关。表示为：
$$s_{k+1}=T_k(s_k,u_k(s_k))$$
  多阶段决策过程的状态转移方程。

2.7指标函数

衡量策略或子策略或决策效果的某种数量指标——指标函数。如奖励函数。

阶段指标函数

$g_k(s_k,u_k)$表示$k$阶段处于$s_k$状态下执行$u_k(s_k)$决策的指标。强化学习中的即时奖励$r$。
$R_k(s_k,u_k)$表示$k$子过程的指标函数。与$s_k$和$p_k(s_k)$有关，严格可表示为$R_k(s_k,p_k(s$

动态规划简介

求算法。。noip动态规划的题。。。。要C语言的!!!!!!!!

求动态规划0-1背包算法解释

算法动态规划 ② ( 动态规划四要素 | 动态规划状态 State | 动态规划初始化 Initialize | 动态规划方程 Function | 动态规划答案 Answer )

算法动态规划 ② ( 动态规划四要素 | 动态规划状态 State | 动态规划初始化 Initialize | 动态规划方程 Function | 动态规划答案 Answer )

算法动态规划 - 斐波那契数