Pytorch autograd.grad与autograd.backward详解

Posted 2023-04-02 Adenialzz

Pytorch autograd.grad与autograd.backward详解

引言

平时在写 Pytorch 训练脚本时，都是下面这种无脑按步骤走：

outputs = model(inputs)		# 模型前向推理
optimizer.zero_grad()		# 清除累积梯度
loss.backward()				# 模型反向求导
optimizer.step()			# 模型参数更新

对用户屏蔽底层自动微分的细节，使得用户能够根据简单的几个 API 将模型训练起来。这对于初学者当然是极好的，也是 Pytorch 这几年一跃成为最流行的深度学习框架的主要原因：易用性。

但是，我们有时需要深究自动微分的机制，比如元学习方法 MAML （参考 Pytorch 代码）中，需要分别根据支持集和查询集的梯度按照不同的策略更新模型参数。这时还是需要了解一些 Pytorch 框架的自动微分机制。幸运的是，Pytorch 关于这部分的框架设计也很清晰，在参考了几个博客之后，笔者将自己的对 Pytorch 自动微分机制接口总结在这里。

注意只是自动微分机制的 Python 接口，而非底层实现。

背景知识

计算图

当今主流深度学习框架的计算图主要有两种形式：静态图（TensoFlow 1.x、Caffe …）和动态图（Pytorch …）。两者的却别简单说来就是：静态图是在模型确定之后就先生成一张计算图，然后每次对于不同的输入样本，都直接丢到计算图中跑；而动态图则是对于每次样本输入都重新构建一张计算图。从它们的区别也可以感受到它们彼此最重要的优劣势：静态图速度快但是不够灵活，动态图灵活但速度稍慢。

在今天，各个框架中动态图与静态图的区分也没有那么绝对了。比如 TensorFlow 2.0 已经采用动态图，而 Pytorch 也可通过 scripting/tracing 转换成 JIT torchscript 静态图。但这不是本文的重点，对深度学习框架计算图感兴趣可参考：机器学习系统:设计与实现 计算图。

我们要讨论的是 Pytorch 的自动微分机制，Pytorch 中主要是动态图，即计算图的搭建和计算是同时的，对每次输入都是重新建图计算。在 Pytorch 的计算图里有两种元素：数据（tensor）和 运算（operation）。

• 运算：包括了加减乘除、开方、幂指对、三角函数等可微分运算。
• 数据：在 Pytorch 中，数据的形式一般就是张量 torch.Tensor。

tensor

Pytorch 中 tensor 具有如下属性：

• requires_grad：是否需要求导

  • 关于 requires_grad 属性的默认值。自己定义的叶子节点默认为 False，而非叶子节点默认为 True，神经网络中的权重默认为 True。判断哪些节点是True/False 的一个原则就是从你需要求导的叶子节点到 loss 节点之间是一条可求导的通路，这条通路上的节点的 requires_grad 都应当是 True。

• grad_fn：当前节点是经过什么运算（如加减乘除等）得到的

• grad：导数值

• data：tensor 的数据

• is_leaf：是否为叶子节点

  • 其他几个概念都比较好理解，这里解释一下什么是叶子节点。

  • 在 Pytorch 中，如果一个张量的 requires_grad=True，则进一步可分为：叶子节点和非叶子节点。叶子节点是用户创建的节点，不依赖其它节点，非叶子结点则是由叶子结点计算得到的中间张量。

    a = torch.randn(2, 2).requires_grad_()
    b = a * 2
    print(a.is_leaf, b.is_leaf)
    # 输出：True False
    

  • 对于 requires_grad=False 的 tensor 来说，我们约定俗成地把它们归为叶子张量。但其实无论如何划分都没有影响，因为张量的 is_leaf 属性只有在需要求导的时候才有意义。

  • 由于叶子节点是用户创建的，所以它的 grad_fn 为空，而非叶子节点都是经过运算得到的，所以 grad_fn 非空

  • 叶子/非叶子表现出来的区别在于：反向传播结束之后，非叶子节点的梯度会被释放掉，只保留叶子节点的梯度，这样就节省了内存。如果想要保留非叶子节点的梯度，可以使用 retain_grad() 方法。

关于 Pytorch tensor 的更多细节，可参考：浅谈 PyTorch 中的 tensor 及使用 。

一个例子

以下例子来自：PyTorch 的 Autograd。

了解过背景知识之后，现在我们来看一个具体的计算例子，先用最常见的梯度反传方式 loss.backward() ，并画出它的正向和反向计算图。假如我们需要计算这么一个模型：

l1 = input x w1
l2 = l1 + w2
l3 = l1 x w3
l4 = l2 x l3
loss = mean(l4)

这个例子比较简单，涉及的最复杂的操作是求平均，但是如果我们把其中的加法和乘法操作换成卷积，那么其实和神经网络类似。我们可以简单地画一下它的计算图，其中绿色节点表示叶子节点：

图1：正向计算图

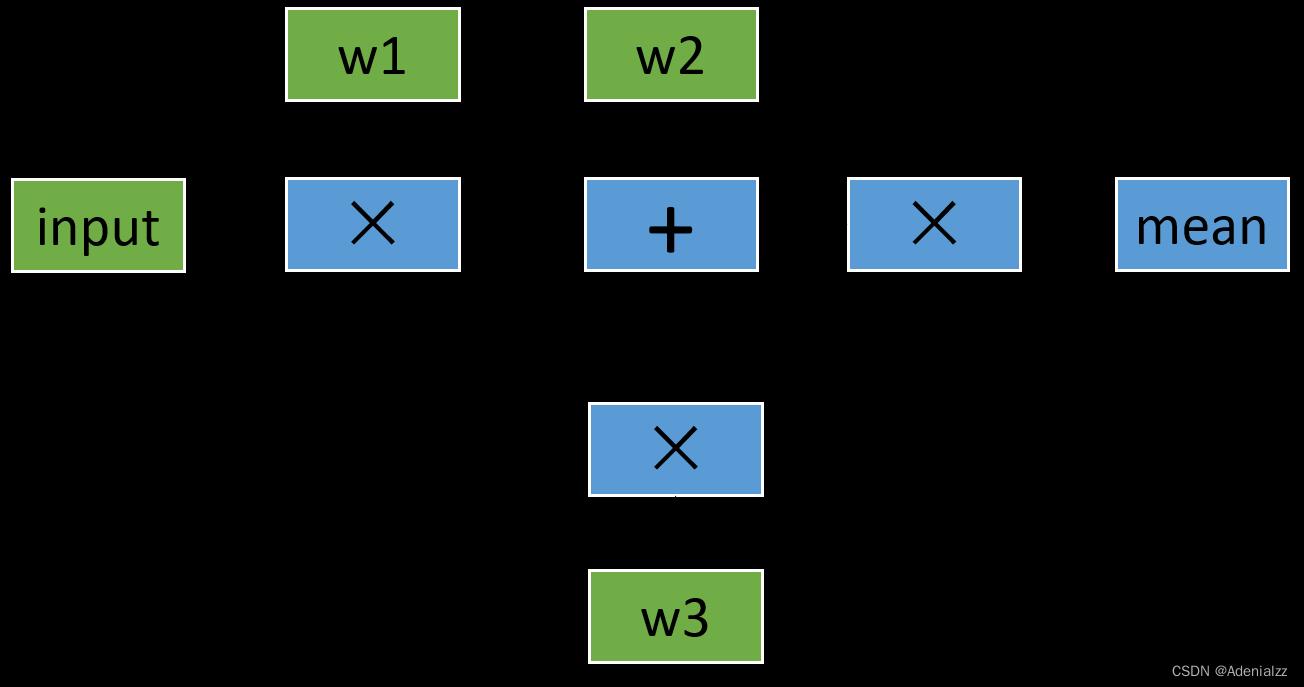
下面给出了对应的代码，我们定义了 input，w1，w2，w3 这三个变量，其中 input 不需要求导结果。根据 Pytorch 默认的求导规则，对于 l1 来说，因为有一个输入需要求导（也就是 w1 需要），所以它自己默认也需要求导，即 requires_grad=True（即前面提到的 ”是否在需要求导的通路上“ ，如果对这个规则不熟悉，欢迎参考 浅谈 PyTorch 中的 tensor 及使用 或者直接查看 官方 Tutorial 相关部分）。在整张计算图中，只有 input 一个变量是 requires_grad=False 的。正向传播过程的具体代码如下：

input = torch.ones([2, 2], requires_grad=False)
w1 = torch.tensor(2.0, requires_grad=True)
w2 = torch.tensor(3.0, requires_grad=True)
w3 = torch.tensor(4.0, requires_grad=True)

l1 = input * w1
l2 = l1 + w2
l3 = l1 * w3
l4 = l2 * l3
loss = l4.mean()

print(w1.data, w1.grad, w1.grad_fn)
# tensor(2.) None None

print(l1.data, l1.grad, l1.grad_fn)
# tensor([[2., 2.],
#         [2., 2.]]) None <MulBackward0 object at 0x000001EBE79E6AC8>

print(loss.data, loss.grad, loss.grad_fn)
# tensor(40.) None <MeanBackward0 object at 0x000001EBE79D8208>

正向传播的结果基本符合我们的预期。我们可以看到，变量 l1 的 grad_fn 储存着乘法操作符 <MulBackward0>，用于在反向传播中指导导数的计算。而 w1 是用户自己定义的，不是通过计算得来的，所以其 grad_fn 为空；同时因为还没有进行反向传播，grad 的值也为空。接下来，我们看一下如果要继续进行反向传播，计算图应该是什么样子：

图2：反向计算图

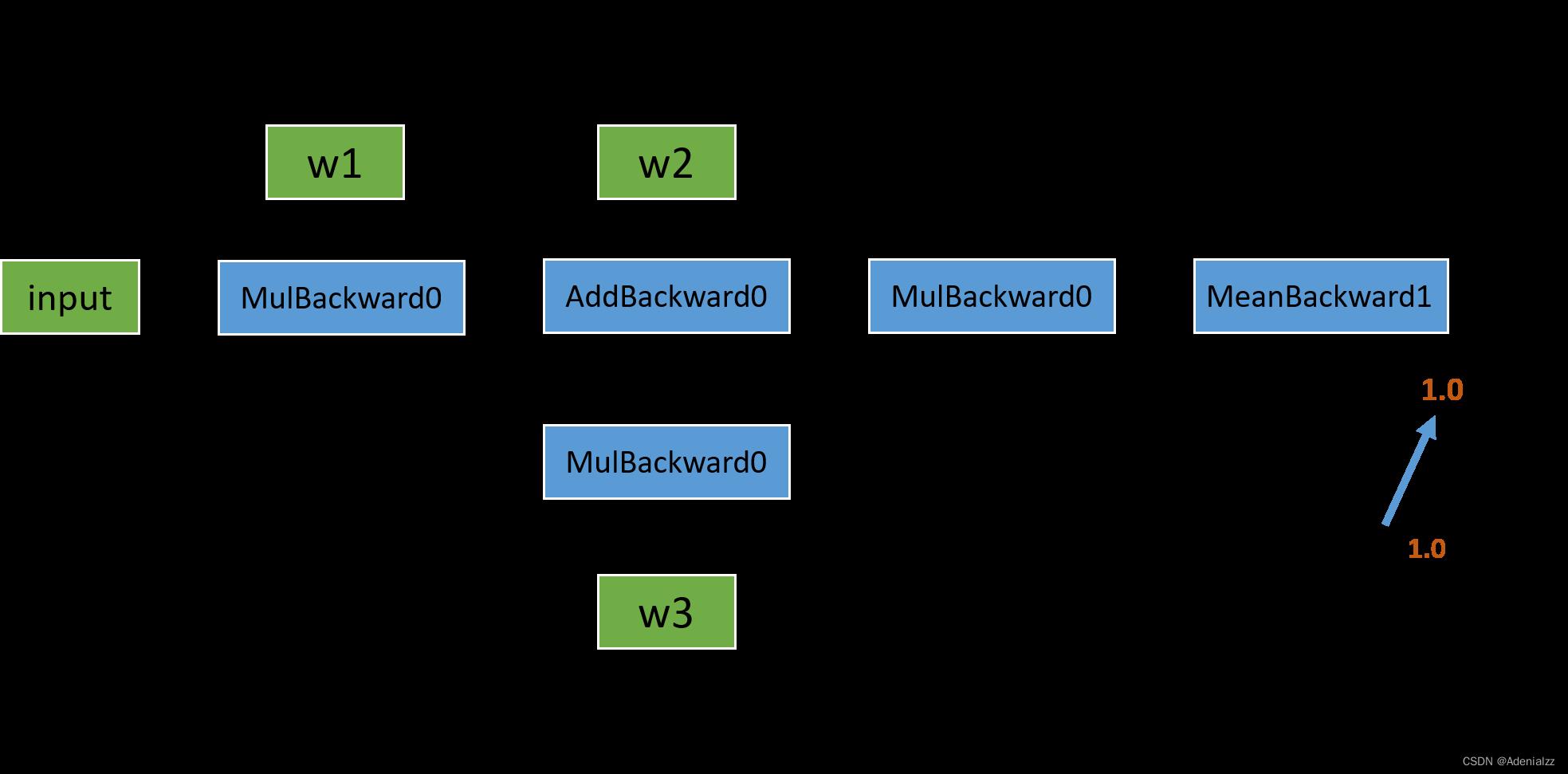
反向图也比较简单，从 loss 这个变量开始，通过链式法则，依次计算出各部分的导数。说到这里，我们不妨先自己手动推导一下求导的结果，再与程序运行结果作对比。如果对这部分不感兴趣的读者，可以直接跳过。

再摆一下公式：

input = [1.0, 1.0, 1.0, 1.0]
w1 = [2.0, 2.0, 2.0, 2.0]
w2 = [3.0, 3.0, 3.0, 3.0]
w3 = [4.0, 4.0, 4.0, 4.0]

l1 = input x w1 = [2.0, 2.0, 2.0, 2.0]
l2 = l1 + w2 = [5.0, 5.0, 5.0, 5.0]
l3 = l1 x w3 = [8.0, 8.0, 8.0, 8.0] 
l4 = l2 x l3 = [40.0, 40.0, 40.0, 40.0] 
loss = mean(l4) = 40.0

首先 $loss=\frac{1}{4}{\sum }_{i=0}^3{l}_4^i$ , 所以 $loss$ 对 $l_4^i$ 的偏导分别为 $\frac{\partial loss}{\partial l_4^i}=\frac{1}{4}$ ;

接着 $\frac{\partial l_4}{\partial l_3}=l_2=[5.0,5.0,5.0,5.0]$ , 同时 $\frac{\partial l_4}{\partial l_2}=l_3=[8.0,8.0,8.0,8.0]$ ;

现在看 $l_3$ 对它的两个变量的偏导：

$\frac{\partial l_3}{\partial l_1}=w3=[4.0,4.0,4.0,4.0]$，$\frac{\partial l_3}{\partial w_3}=l1=[2.0,2.0,2.0,2.0]$

因此 $\frac{\partial loss}{\partial w_3}=\frac{\partial loss}{\partial l_4}\frac{\partial l_4}{\partial l_3}\frac{\partial l_3}{\partial w_3}=[2.5,2.5,2.5,2.5]$ , 其和为 10 ;

同理，再看一下求 $w_2$ 导数的过程： ∂ l o s s ∂ w 2 = ∂ l o s s ∂ l 4 ∂ l 4 ∂ l 2 ∂ l 2 ∂ w 3 = [ 2.0 , 2.0 , 2.0 , 2.0 ] \\frac\\partial loss\\partial w_2=\\frac\\partial loss\\partiall_4\\frac\\partiall_4\\partiall_2\\frac\\partiall_2\\partial w_3=[2.0,2.0,2.0,2.0] ∂w2​∂loss​=∂l4​∂loss​∂l2​∂l4​​∂w3​∂lPytorch. Can autograd be used when the final tensor has more than a single value in it?的可能重复 【参考方案1】：

让我们从简单的工作示例开始，该示例具有普通的损失函数和常规的后向。我们将构建一个简短的计算图并对其进行一些梯度计算。

代码：

import torch
from torch.autograd import grad
import torch.nn as nn


# Create some dummy data.
x = torch.ones(2, 2, requires_grad=True)
gt = torch.ones_like(x) * 16 - 0.5  # "ground-truths" 

# We will use MSELoss as an example.
loss_fn = nn.MSELoss()

# Do some computations.
v = x + 2
y = v ** 2

# Compute loss.
loss = loss_fn(y, gt)

print(f'Loss: loss')

# Now compute gradients:
d_loss_dx = grad(outputs=loss, inputs=x)
print(f'dloss/dx:\n d_loss_dx')

输出：

Loss: 42.25
dloss/dx:
(tensor([[-19.5000, -19.5000], [-19.5000, -19.5000]]),)

好的，这行得通！现在让我们尝试重现错误“grad can be implicitly created only for scalar outputs”。如您所见，前面示例中的损失是一个标量。 backward() 和 grad() 默认处理单个标量值：loss.backward(torch.tensor(1.))。如果你尝试传递更多值的张量，你会得到一个错误。

代码：

v = x + 2
y = v ** 2

try:
    dy_hat_dx = grad(outputs=y, inputs=x)
except RuntimeError as err:
    print(err)

输出：

grad can be implicitly created only for scalar outputs

因此，使用grad()时需要指定grad_outputs参数，如下：

代码：

v = x + 2
y = v ** 2

dy_dx = grad(outputs=y, inputs=x, grad_outputs=torch.ones_like(y))
print(f'dy/dx:\n dy_dx')

dv_dx = grad(outputs=v, inputs=x, grad_outputs=torch.ones_like(v))
print(f'dv/dx:\n dv_dx')

输出：

dy/dx:
(tensor([[6., 6.],[6., 6.]]),)

dv/dx:
(tensor([[1., 1.], [1., 1.]]),)

注意：如果您改用backward()，只需使用y.backward(torch.ones_like(y))。

【讨论】：

不错的答案，但grad_outputs 的一般含义是什么？在某些情况下我们需要使用 grad_outputs=torch.ones_like(outputs) 以外的东西吗？如果解决方案始终相同，为什么grad 不简单地假设grad_outputs=torch.ones_like(outputs) 而不是抛出错误？