博弈论在电动车和电网系统中分布式模型预测控制研究（Matlab代码实现）

Posted 2023-04-02 然哥依旧

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 文献来源

🌈4 Matlab代码、数据、文章讲解

---

💥1 概述

电动汽车（EV）将在未来的交通系统中广泛使用。尽管这些电动汽车不受控制的充电将威胁电网的稳定性，但兼容的能源交易政策可以为电网提供有益的服务，并保持系统的可持续性。本文利用大宗费率关税，引入了批发定价政策。利用多目标方法同时解决成本降低和负载均衡服务的问题。由于集中式问题的计算复杂度很高，因此采用了博弈论方法来设计电动汽车的分散控制器。此外，引入了MPC方法，以处理未来几个小时内系统状态的计划外偏差。仿真结果验证了所提方法能够有效改造系统性能。

分布式发电作为解决现代城市未来电网问题的关键解决方案，在过去几年中得到了极大的关注[1]。随着过去几十年双向充电器的快速发展，电动汽车充电和放电的想法已经发展出一种新颖的车辆到电网（V2G）系统概念。在V2G系统中，在电动汽车中实现的电池被视为可被电力系统利用的移动储能，以提供各种辅助服务，如负载均衡、调峰、频率调节等。到电网。这些服务的主要思想源于这样一个事实，即电动汽车可以在非高峰时段充电并在关键时段放电，为电网提供所需的能量[2]。但是，只有当有许多电动汽车车主有兴趣参与此类服务时，所有 V2G 服务才可能随时可用。通过参与V2G辅助服务来降低充电成本和提供收入是两个有效的鼓励措施，可以说服电动汽车车主为V2G服务做出贡献[3]。

在最近的文献中，已经引入了许多基于优化的方法，例如线性规划（LP）和二次规划（QP）来解决电动汽车充电管理问题。在[4]中，作者提出了一个LP问题，以最小化电动汽车车主的充电成本并最大化聚合商的利润。负载均衡服务在 [5] 中被解释为 QP 问题，以最小化电网负载曲线的方差。[6]中讨论了未来小时电价和需求的不确定性，作者提出了一种模型预测控制（MPC）方法来处理频率调节服务中的这个问题。在[2]中探讨了考虑V7G系统中目标冲突的想法，其中采用了加权和方法来解决多目标优化问题，其中提供谷填充服务以及降低充电成本。

博弈论作为对像V2G这样的复杂系统代理之间的相互作用进行建模的令人信服的发明，已被作者有效地应用于[8]来解决负载均衡问题解决方案的计算复杂性。本研究将负载均衡服务的集中解转化为相应博弈的均衡收敛到原集中式负载均衡问题的解的分散问题。电力需求、电价以及电动汽车在充电站（或智能建筑）中的存在和参数等未来小时信息的不确定性是这项工作中缺失的组成部分。此外，电动汽车的电费和充电成本在[8]中没有考虑。

本文的主要贡献是提供一个分布式框架，以解决V2G系统的冲突目标，例如在未来小时信息存在不确定性的情况下降低充电成本和负载均衡服务。为此，我们应用了一种通用的博弈论方法来解决MPC框架中相应的多目标问题。

📚2 运行结果

 

 

 

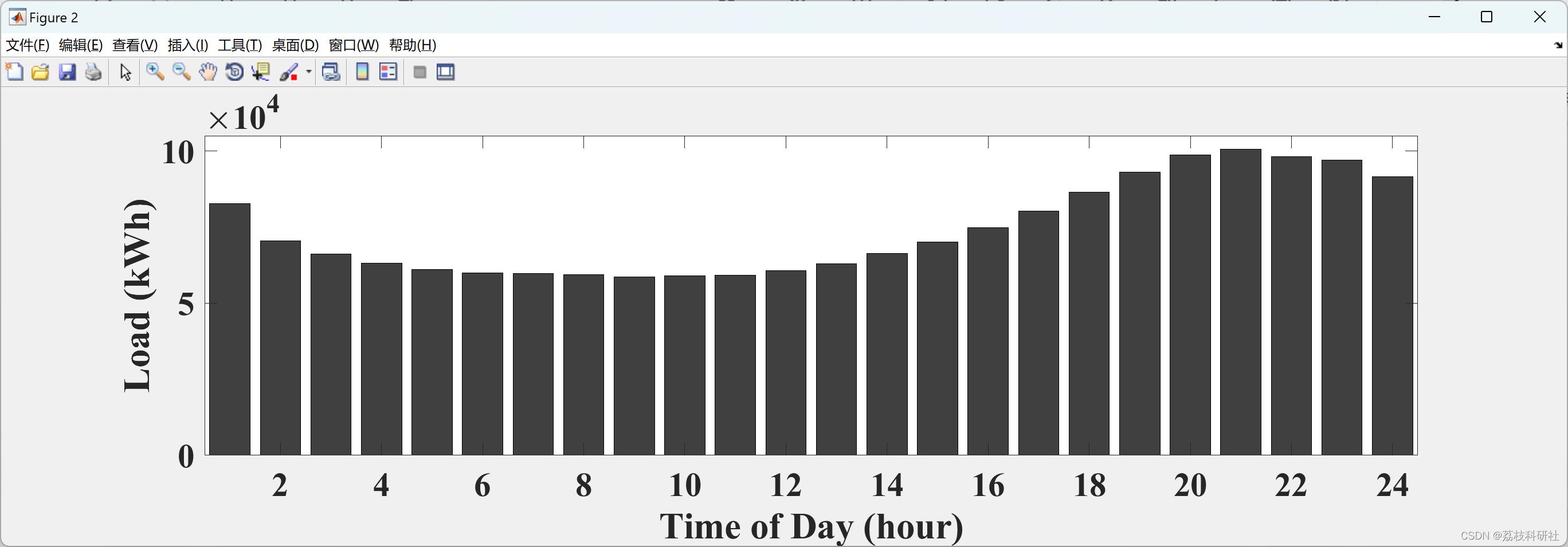
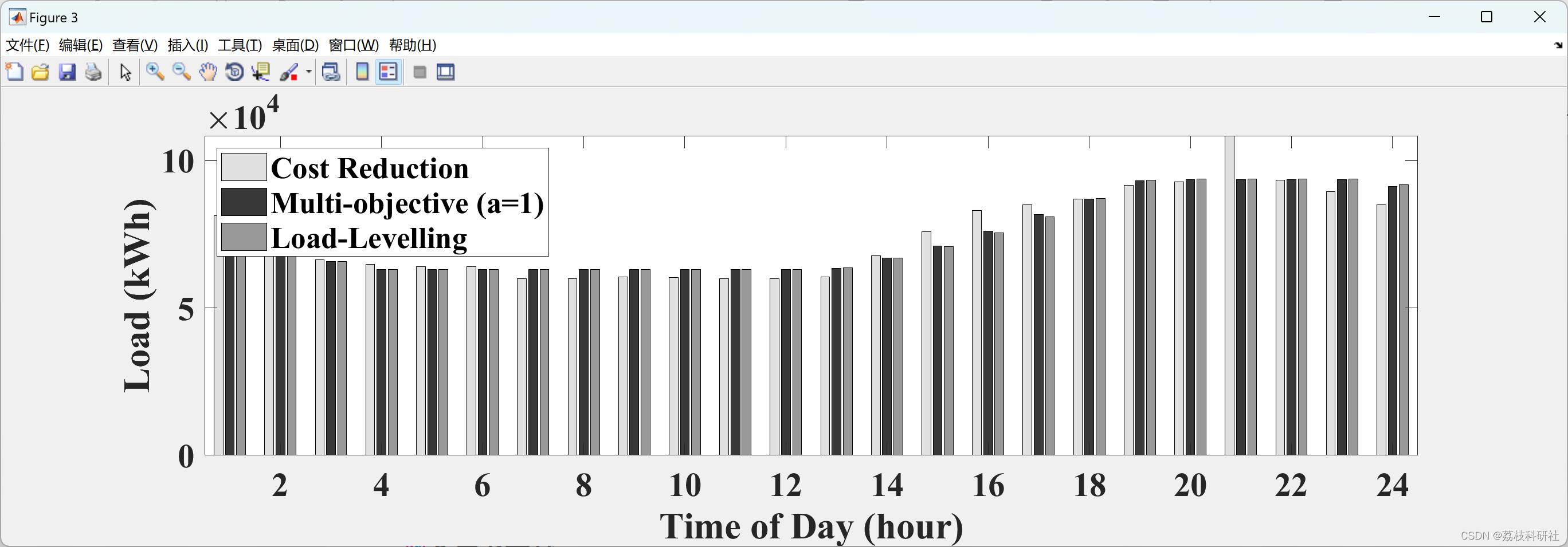
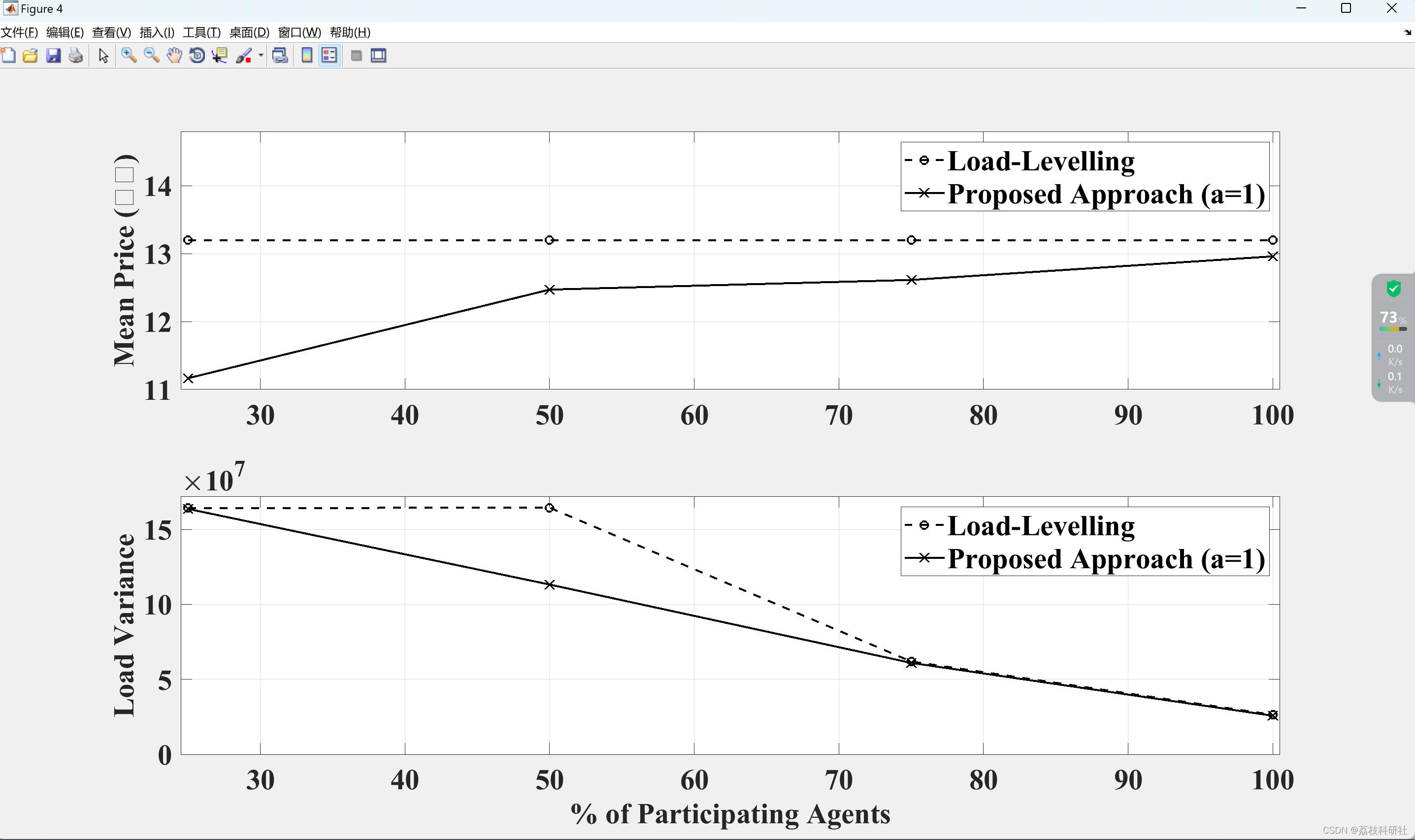
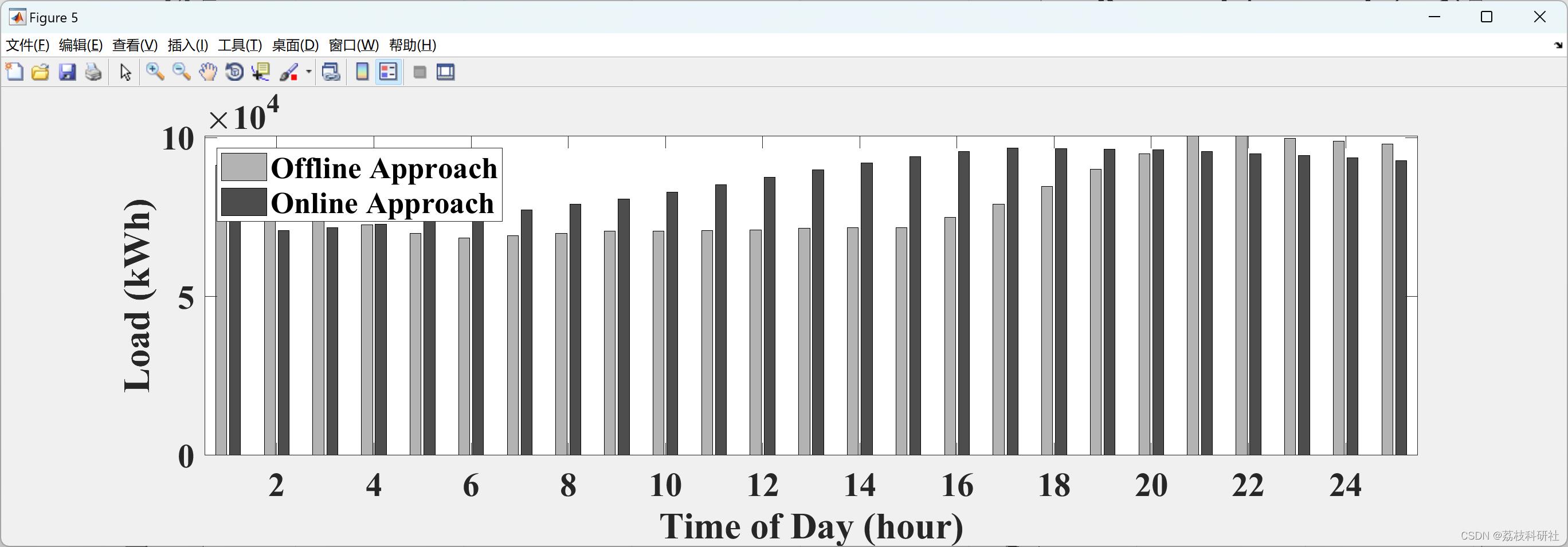
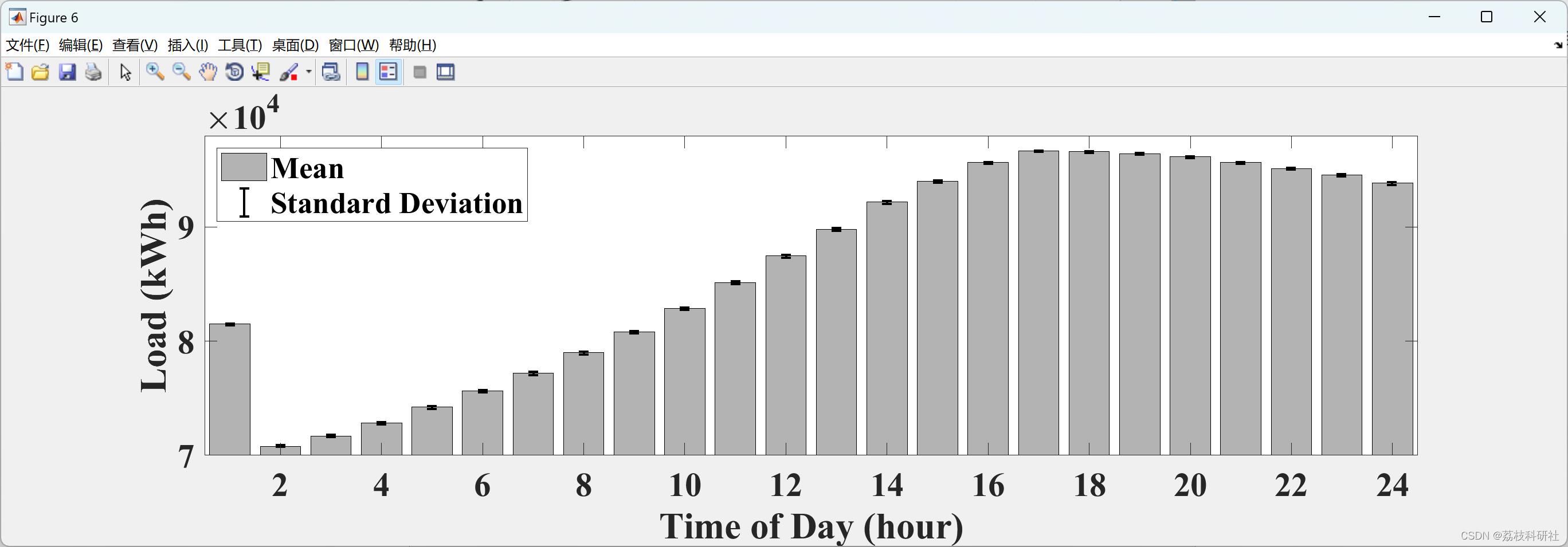
部分代码：

F2 = figure(2);
F2.WindowState = 'maximized';
F2.Position = [1,1,1366,400];
B_Fig2 = bar(L_Fig2);
B_Fig2.FaceColor = [0.25 0.25 0.25];
set(findall(gcf,'-property','FontSize'),'FontSize',22);
set(findall(gcf,'-property','FontWeight'),'FontWeight','Bold');
set(findall(gcf,'-property','FontName'),'FontName','Times New Roman');
xlabel('Time of Day (hour)');
xticks(2:2:24);
xlim([0.5 24.5]);
ylim([0 105000]);
ylabel('Load (kWh)');

%% Fig 3

L0 = load('Fig3_L.mat');

L_Fig3 = L0.Fig3_L;

F3 = figure(3);
F3.WindowState = 'maximized';
F3.Position = [1,1,1366,400];
B_Fig3 = bar(L_Fig3);
B_Fig3(1).FaceColor = [0.88 0.88 0.88];
B_Fig3(2).FaceColor = [0.22 0.22 0.22];
B_Fig3(3).FaceColor = [0.6 0.6 0.6];
set(findall(gcf,'-property','FontSize'),'FontSize',18);
set(findall(gcf,'-property','FontSize'),'FontSize',22);
set(findall(gcf,'-property','FontWeight'),'FontWeight','Bold');
set(findall(gcf,'-property','FontName'),'FontName','Times New Roman');
xlabel('Time of Day (hour)');
xticks(2:2:24);
xlim([0.5 24.5]);
ylabel('Load (kWh)');
legend('Cost Reduction','Multi-objective (a=1)','Load-Levelling','Location','northwest');

%% Figure 4

L11_5000 = load('L_1_1_5000.mat');
L11_10000 = load('L_1_1_10000.mat');
L11_15000 = load('L_1_1_15000.mat');
L11_20000 = load('L_1_1_20000.mat');

🎉3 文献来源

部分理论来源于网络，如有侵权请联系删除。

[1]Arash Karimi (2021) A Game Theoretic Approach to Distributed Model-Predictive Control of Smart Grids

🌈4 Matlab代码、数据、文章讲解

微电网优化基于matlab粒子群优化算法的微电网调度(光伏储能电动车电网交互)含Matlab源码 2190期

一、粒子群算法求解电联供型微电网经济运行优化简介

0 引言
热电联供 (combined heat and power, CHP) 系统建立在能源梯级利用的概念基础上, 统一解决了电能和热能的供应问题, 是一种经济节能、环境友好的用能方式, 具有良好的社会和经济效益, 在国内外引起广泛关注。在发展低碳绿色经济的背景下, 中国也开始重视CHP系统的发展, 但技术还不成熟, 应用尚处于起步阶段。

CHP型微网是一个复杂的能量系统, 存在多种能量平衡关系。在满足用户热电负荷需求的前提下, 如何根据微源配置 (即参与微源的种类、微源的运行参数等) 制定系统未来一段时间内的运行方案 (即各微源在各时段的功率分配) , 以使系统获得最佳经济效益, 是微网经济运行研究中的一个重要内容。目前, 国内的研究还仅局限在电力微网的层面上, 对CHP系统涉及较少, 国外在此方面已有相关研究展开。文献针对由风电机组和质子交换膜型燃料电池组成的CHP系统, 利用进化算法研究该系统的经济运行问题, 比较了对回收的热能采取4种不同方案得到的结果。研究了由燃气轮机、吸附式制冷机和余热锅炉构成的冷热电三联供系统, 建立简单的线性模型, 对系统运行策略进行优化。以成本最小化为目标, 建立了CHP型微网中各种类型微源的优化配置模型, 并采用粒子群优化 (PSO) 算法进行求解。

本文建立了一种含可再生能源的CHP型微网系统, 由风电机组、光伏电池、燃料电池、余热锅炉、燃气锅炉、蓄电池等微源和热电负荷构成。由于风电、光伏功率以及热电负荷存在很强的随机性, 而且目前的预测水平还远未达到实际应用的要求, 因此这些量将作为未知因素考虑。

1 含可再生能源的CHP型微网系统
本文研究的含可再生能源的CHP型微网系统如图1所示。

图1 含可再生能源的CHP型微网系统
风电机组和光伏电池分别以风能和太阳能为原动力, 作为可再生能源接入微网;燃料电池和燃气锅炉以天然气为燃料, 将化学能直接转化为电能和热能;余热锅炉回收燃料电池产生的废热;蓄电池作为储能装置, 根据系统运行情况, 实时进行充放电。此系统还与大电网进行双向的电功率流动, 当电能不足时从大电网购买电能, 当电能富足时向大电网销售电能。整个系统分成2个部分:用户电负荷由风电机组、光伏电池、燃料电池供给, 并可与大电网和蓄电池进行双向功率交换;用户热负荷由燃气锅炉和余热锅炉供给。

2 CCP理论
CCP主要针对约束条件中含有随机变量, 且必须在观测到随机变量的实现之前作出决策的情况。考虑到所作决策在不利的情况发生时可能不满足约束条件而采取一种原则:允许所作决策在一定程度上不满足约束条件, 但是该决策应该使约束条件成立的概率不小于某一置信水平。
考虑带有随机参数的数学规划模型:

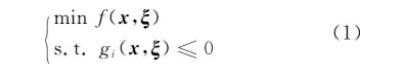
式中:x为决策向量;ξ为随机向量;f (x, ξ) 为目标函数;gi (x, ξ) 为随机约束函数;i=1, 2, …, q。
实际上, 由于随机变量ξ使得目标函数和约束条件的含义并不明确, 因此上述规划模型没有意义。
CCP解决了上述问题, 其模型如下:

式中:Pr表示括号中事件成立的概率;α和β分别为事先给定的约束条件和目标函数的置信水平;f-为目标函数f (x, ξ) 在置信水平至少为β时所取的最小值。

3 含可再生能源的CHP型微网经济运行优化模型
本文应用CCP理论建立了含可再生能源的CHP型微网经济运行优化模型, 以系统运行费用最小化为目标, 综合考虑系统的能量平衡约束以及各微源的运行约束, 对系统的运行方案进行优化。

3.1 目标函数
系统运行费用包括:从大电网购电的费用;燃料电池、燃气锅炉的天然气使用费用;风电机组、光伏电池、燃料电池、余热锅炉、燃气锅炉、蓄电池等微源的维护费用;向大电网售电的收入。由于目标函数中含有风电、光伏功率等随机变量, 运行费用也是一个随机量, 因此采用确定性的表达式没有意义。根据式 (2) , 目标函数表示如下:

T为单位时段的时间间隔;n为时段总数;Pex, i为第i时段与大电网交换的电功率, 购电为正, 售电为负;Pfl, i为第i时段燃料电池的发电功率;Pgb, i为第i时段燃气锅炉功率;Pbt, i为第i时段蓄电池充放电功率, 放电为正, 充电为负;Pwt, i为第i时段风电机组功率;Ppv, i为第i时段光伏电池功率;Cph为从大电网购电的价格;Cse为向大电网售电的价格;Cgas为天然气价格;Cfl_om为燃料电池维护费用;Cbl_om为余热锅炉维护费用;Cgb_om为燃气锅炉维护费用;Cbt_om为蓄电池维护费用;Cwt_om为风电机组维护费用;Cpv_om为光伏电池维护费用;ηfl, i为燃料电池第i时段的效率;rfl, i为燃料电池第i时段的热电比值;ηgb为燃气锅炉的效率;ηhr_bl为余热锅炉废热回收效率。

3.2 约束条件
约束条件包括电能、热能的平衡约束以及各微源的运行约束。

1. 电能平衡约束
   电能平衡约束根据蓄电池充电与放电情况分为如下2种:
   
   式中:Pel, i为第i时段的电负荷;ηch和ηdis分别为蓄电池充放电效率;i=1, 2, …, n, 下同。

2. 热能平衡约束
   
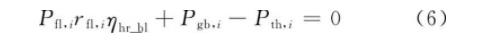
   式中:Pth, i为第i时段的热负荷。

3. 与大电网功率交换约束
   
   式中:Pex, max和Pex, min分别为与大电网功率交换的最大和最小值, 即向大电网购电和售电的最大功率。

4. 燃料电池运行约束
   
   式中:ΔPfl_up和ΔPfl_down分别为燃料电池单位时段内功率最大增发量和最大减发量;Pfl, max和Pfl, min分别为燃料电池的最大和最小发电功率。

5. 余热锅炉运行约束
   
   式中:Pbl, max和Pbl, min分别为余热锅炉的最大和最小功率。

6. 燃气锅炉运行约束
   
   式中:Pgb, max和Pgb, min分别为燃气锅炉的最大和最小功率。

7. 蓄电池运行约束
   
   式中:j=1, 2, …, n;Pbt, min和Pbt, max分别为蓄电池的最大充放电功率;Wbt, max和Wbt, min分别为蓄电池的最大和最小储能量;式 (13) 表示蓄电池最终储能量与初始储能量Winit相等。

3.3 含随机变量的约束条件处理方法
与传统的优化方法不同, 由于风电、光伏功率以及热电负荷具有随机性, 某些约束条件不再具有确定性。本文根据CCP理论建立模型, 对含有随机变量的不等式约束, 以概率的形式进行描述, 使其能够在一定的置信水平下成立。置信水平的设置根据系统实际的运行要求进行。

根据等式约束 (式 (4) ~式 (6) 和式 (13) ) , 可将Pex, i, Pgb, i表示为含有Pwt, i, Ppv, i, Pel, i, Pth, i等随机变量的函数。一方面消去模型中的等式约束, 将原问题转化为只含有不等式约束的新问题, 便于PSO算法求解过程中的粒子可行性的检验。同时, Pex, i, Pgb, i成为随机量, 因此, 不等式约束 (式 (7) 和式 (11) ) 可以用概率形式描述为:

4 基于随机模拟的PSO算法
4.1 随机模拟
CCP相比于确定性规划的难点在于如何处理机会约束, 如果机会约束比较容易处理, 则可以将机会约束转化为各自的确定性等价类, 然后利用传统方法求解其等价的确定性模型。对于复杂的机会约束, 可以引入随机模拟技术进行处理。

随机模拟, 即Monte Carlo模拟, 其基础是从已知的概率分布中对随机变量进行抽样, 从而为系统决策提供依据或对系统决策进行检验。在求解上述优化模型过程中, 主要在两处引入了随机模拟技术。

1. 计算目标函数值
   对于带有随机变量ξ的目标函数:
   
   随机模拟算法如下:①根据随机变量ξ的概率分布Φ (ξ) , 生成N个独立的随机向量ξi (i=1, 2, …, N) ;②置fi=f (x, ξi) ;③取N′=βN, 根据大数定律, 取序列f1, f2, …, fN中第N′个最小的元素作为目标函数值。

2. 检验机会约束
   对于带有随机变量ξ的机会约束:
   
   随机模拟算法如下:①置计数器N′=0;②根据随机变量ξ的概率分布Φ (ξ) 生成随机变量ξ;③如果g (x, ξ) ≤0成立, 则N′=N′+1;④重复步骤②和③共N次;⑤;果N′/N≥α, 则机会约束成立, 否则不成立。

4.2 算法流程
PSO算法于1995年被首次提出[19], 具有概念简单、易于实现、调整参数少、收敛速度快、鲁棒性能强等优点, 已逐步渗透到各个应用领域, 并得到广泛应用。文献[20]对PSO算法作了详细介绍, 本文不再赘述。
根据以上模型, 提出基于随机模拟的PSO算法流程如下。
步骤1:输入各微源运行参数、各种费用参数和风电、光伏功率以及热电负荷等随机变量的分布参数。
步骤2:设置目标函数以及含随机变量的约束条件的置信水平;设置PSO算法参数, 包括粒子数、最大迭代次数、学习因子、初始惯性权重、终止惯性权重等。
步骤3:根据各时段风电、光伏功率以及热电负荷等随机变量的分布参数, 随机生成各时段的风电、光伏功率以及热电负荷。
步骤4:随机生成各时段燃料电池功率和蓄电池充放电功率, 组成1个粒子, 根据式 (8) ~式 (10) 、式 (12) 、式 (14) ~式 (16) 检验粒子可行性;若粒子不可行, 则重新生成粒子, 直至初始粒子生成完毕, 并同时随机生成各粒子的初始速度;对于如式 (15) 和式 (16) 所示含有随机变量的约束条件, 需根据步骤3中生成的随机量, 利用随机模拟技术检验约束条件是否成立, 即约束条件是否满足置信水平。
步骤5:利用随机模拟技术计算各个粒子的适应值。
步骤6:对每个粒子, 将其适应值与个体极值进行比较, 如果较优, 则更新当前的个体极值和个体最优位置;再将其适应值与全局极值进行比较, 如果较优, 则更新当前的全局极值和全局最优位置。
步骤7:对每个粒子的速度和位置进行更新, 并检验粒子可行性, 方法同步骤4;若粒子不可行, 则重新生成粒子的速度再更新位置, 直至粒子可行。
步骤8:重复步骤5~步骤7, 直至达到最大迭代次数。
步骤9:输出最优解和目标函数最优值。

二、部分源代码

clear all;
clc;
format short;
tic

XDCRL=10; %蓄电池容量
pgridmax=7;%交互功率
m=100; %种群规模数
dd=500; %迭代次数
c1=1;
c2=1;
vmax=1;
vmin=-1;
wmax=0.9;
wmin=0.4;
d=25;%24时刻蓄电池SOC0
CFX =[];%惩罚项
cfx = 0;%惩罚项

PV=load(‘Ppv2.txt’);%光伏发电量
% Pev=zeros(1,24);
Pev=load(‘PEV.txt’);%电动汽车
LOAD= load(‘Load2.txt’);%负荷
sub=load(‘C_sub2.txt’);
buy=load(‘C_buy2.txt’);
sell=load(‘C_sell2.txt’);
xdccl=zeros(m,24);%蓄电池出力
v=zeros(m,d);%初始化速度
SOC=rand(m,d);%蓄电池的SOC
grid=zeros(m,24);%微网
GRID=zeros(1,24);
fx=zeros(1,m);

%%初始化粒子更新
for n=1:m; %每一次更新粒子群（100个粒子）都有判断是否满足条件
for i=2:d %保证蓄电池的SOC大于0.3,小于0.95
if SOC(n,i)<0.3
SOC(n,i)=0.3;
end
if SOC(n,i)>0.95
SOC(n,i)=0.95;
end
SOC(n,1)=0.4;%蓄电池的SOC不变，都为0.4
SOC(n,25)=0.4;%蓄电池的SOC不变，都为0.4
end

三、运行结果

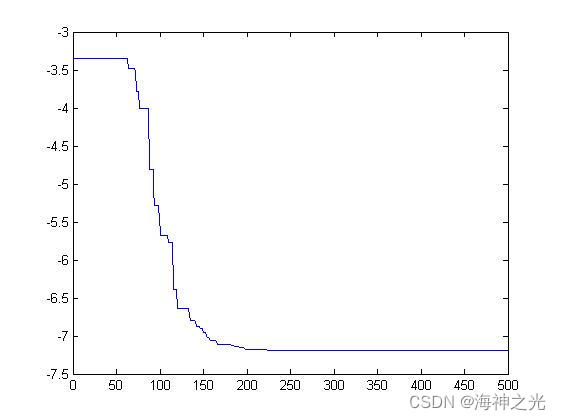
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]王锐,顾伟,吴志.含可再生能源的热电联供型微网经济运行优化[J].电力系统自动化. 2011,35(08)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除