时间序列预测 EViews

Posted 2023-03-31 江尚寒

时间序列预测

 

简述

时间序列预测是对时间序列数据潜在过程观测的结果。由于时间序列数据是具有随机过程的变量，因此，时间序列预测对时间序列数据的挖掘相比于截面数据随机抽样的回归分析更具有充分性。

时间序列数据性质

时间序列数据的主要特征为时间顺序性，是多种动态信息的自然载体。可以反映趋势性、周期性和滞后效应等。

从概率统计的角度，时间序列是一组随机变量在一系列时刻上的样本实现。

依据序列的统计特征是否随时间变化，可分为非平稳序列和平稳序列。如果序列是平稳的，则意味着这组序列两个时刻的相关性都保持稳定。因此，可以基于历史数据呈现出来的统计规律很好地预测未来。反之，如果序列是非平稳的，意味着这组序列两个时刻的相关性不稳定，即对数据产生的影响因素挖掘不正确或不充分，难以预测未来数据。

时域分析法

其基本思想是源于事件的发展通常具有一定的惯性，这种惯性使用统计语言来描述即为序列之间的相关关系。而这种相关关系具有一定的统计性质，时域分析的重点就是寻找这种统计规律，并且拟合恰当的数学模型来描述这种规律，进而利用这个拟合模型来预测序列未来的走势。

事件序列的特征统计量

通常协方差函数和相关系数度量是两个不同事件彼此之间相互影响的程度，而自协方差和相关系数度量的是同一事件在两个不同时期之间的相关程度，即度量自己过去的行为对自己现在的影响。

协方差表示两个变量的总体误差，这与只表示一个变量误差的方差不同。如果两个变量的变化趋势一致（也就是其中一个大于自身的期望值，另一个也大于自身的期望值）那么两个变量的协方差就是正值，反之亦然。

平稳性

宽平稳

宽平稳是使用序列的统计量来定义的一种平稳性，它认为序列的统计性质主要由它的低阶矩（一阶矩是期望值，二阶矩是方差）决定，所以只要保证序列低阶矩平稳就能保证序列的主要性质近似平稳。

条件

1. 序列值平方的期望小于正无穷
2. 均值为常数
3. 两组时间间隔相同的数自协方差函数相等

平稳性的意义

平稳序列的常数均值性质使得均值序列变成常数序列,原来每个的均值只依靠唯一的一个观测值去估计，当整体的均值常数代替原来的均值，每个样本观测值都可以看作均值常数的观测值。因此，平稳序列极大地减少了随机变量地的个数，并增加带估测变量的样本容量，简化了时间序列分析的难度。提高了对特征统计量的估计精度。

平稳性检验

1. 时序图检验：根据平稳序列均值、方差为常数的性质，平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动，而且波动的范围有界，无明显趋势和周期特征。
2. 自相关图检验：平稳序列通常具有短期相关性，该性质通过自相关系数来描述就是随着延迟期数的增加，平稳序列的自相关系数会很快衰减于零。
3. 单位根检验

检验单位根最常用的方法是迪基-高勒检验（ADF)

 

 

随机性检验

白噪声序列的性质

1. 存在均值
2. 不同时刻序列值相关系数为零，同一时刻相关系数等于方差。

反之，若序列呈现比较显著的相关关系，即自相关系数不为零，则说明序列不是纯随机序列。

演示eviews时间序列分析

(数据编的，不要在意）

原始数据可视化

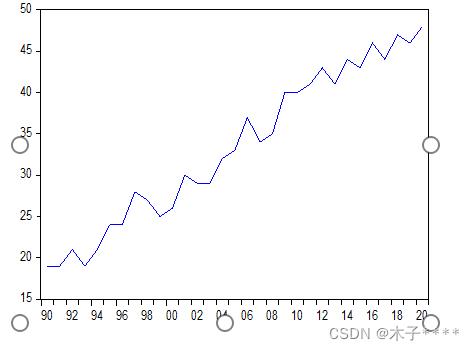
一、单位根检验

单位根检验有以下三种情形:

在eviews操作用，按照情况3-情况2-情况1的顺序进行检验。

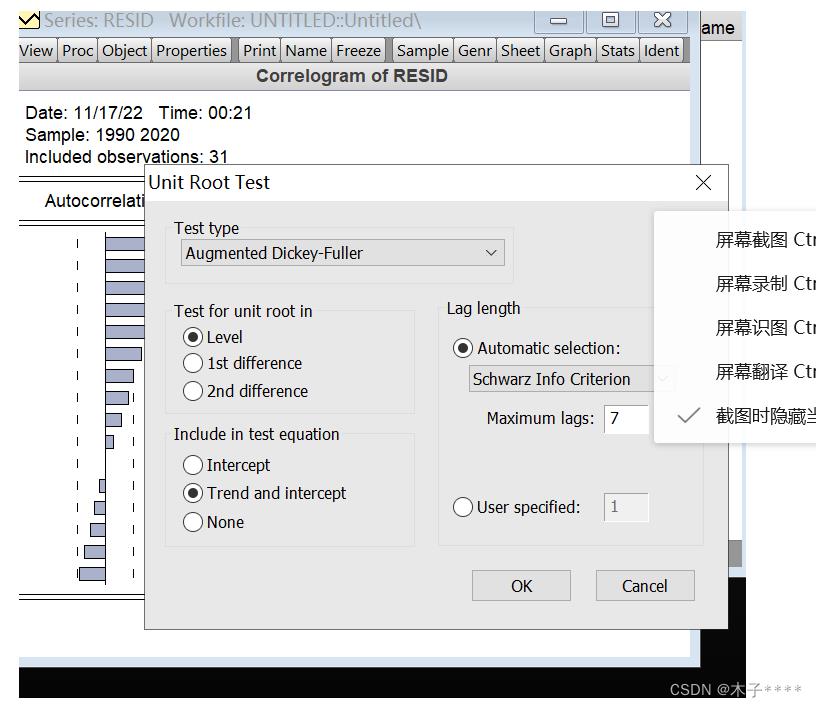
1、View-unit root test--trend and intercept

2、View-unit root test--intercept

3、View-unit root test--none

得到结果如下：

1:

2:

3:

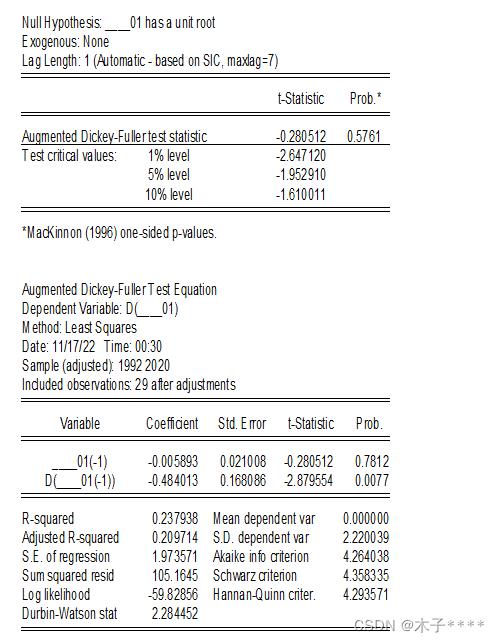
观察第一个表prob值，小于等于0.05代表拒绝原假设即单位根不等于1，模型是平稳的。本题的情况View-unit root test--trend and intercept和View-unit root test--intercept是平稳的。

再根据拟合优度即：对比akaike info criterion;schwarz criterion;hannan-quinn creter三个指标（越小越好），在View-unit root test--trend and intercept和View-unit root test--intercept中选择View-unit root test--intercept。

若序列为特殊情况，未通过平稳性检验，则进行差分来构造平稳序列。通过观察一阶或二阶差分是否通过平稳性检验。若均通过平稳性检验，对比二者的拟合优度选择最合适的模型。

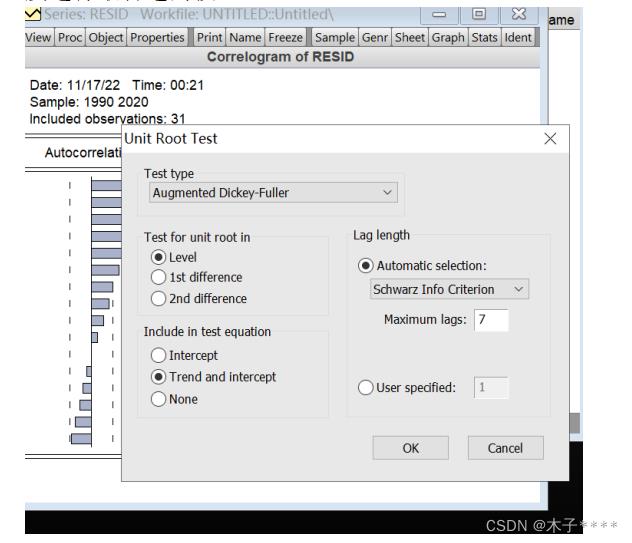
View-unit root test--1st difference

View-unit root test--2nd difference

拟合优度对比通过akaike info criterion;schwarz criterion;hannan-quinn creter三个指标（越小越好）

二、模型识别

 自相关图view-correlogram

：

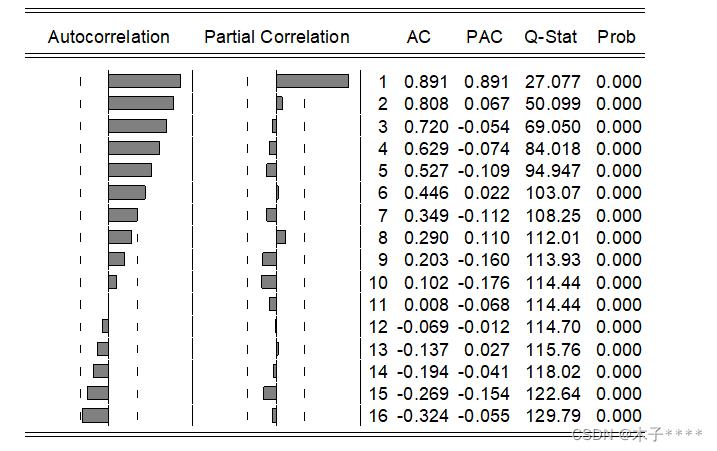
截尾和拖尾的判断：

截尾：在大于某个常数K后快速趋于0的为K阶截尾。

拖尾：始终有非0取值，不会再大于某个常数后就恒等于0（或在0附近波动）

AR：自相关系数拖尾，偏相关系数截尾

MA：自相关系数截尾，偏相关系数拖尾

ARMA：均为拖尾

若相关系数均为0——证明为白噪声序列

通过观察自相关图，可确定为AR模型，因为从n=2开始控制在置信区间之内，初步判断为AR(2)模型。

三、确定滞后阶数

序列相关检验：

序列相关性，在计量经济学中指对于不同的样本值，随机干扰之间不再是完全相互独立的，而是存在某种相关性。又称自相关，是指总体回归模型的随机误差项之间存在相关关系。
如果模型中省略了某些重要的解释变量或者模型函数形式不正确，都会产生系统误差，这种误差存在于随机误差项中，从而带来了自相关。由于设定误差造成的自相关，在经济计量分析中经常可能发生。

向下检验方法：由大到小检验滞后阶数的显著性是否为0。因为初步判断模型为2阶。因此分类建立3阶、2阶、1阶的模型。

时间序列变量命名为x

点击【quick】----【estimate equation】

分别输入：x c x(-3) x(-2) x(-1)

                  x c x(-2) x(-1)

                  x c x(-1)

 对比这三个阶数模型的拟合优度（拟合优度对比通过akaike info criterion;schwarz criterion;hannan-quinn creter三个指标（越小越好））确定3阶模型的拟合优度最好。

自此完成残差序列相关检验。

残差的异方差检验（ARCH检验）

ARCH检验是误差项二阶矩（二阶矩为方差）的自回归过程。

点击【view】--【residual diagnostics】--【heteroskedasticity tests】

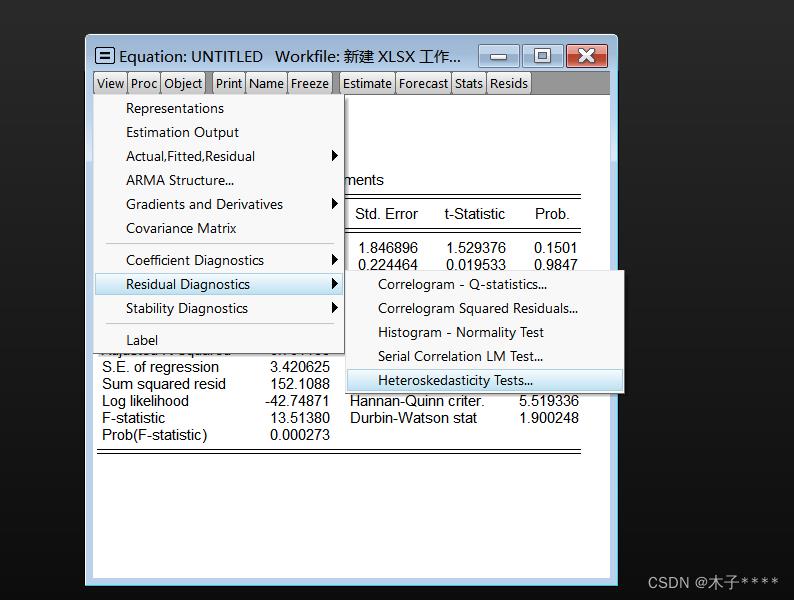
 分别设置滞后阶数为1，2，3.

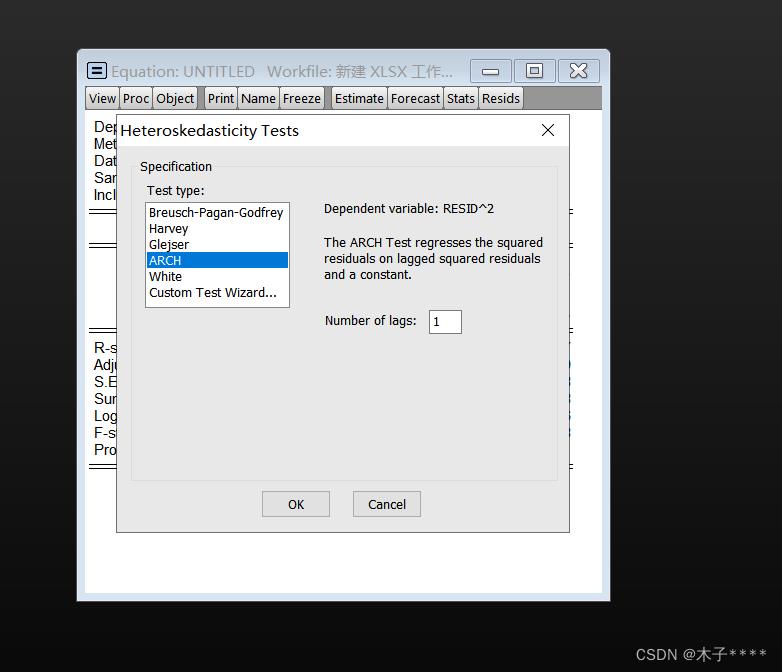
 对比这三个阶数模型的拟合优度（拟合优度对比通过akaike info criterion;schwarz criterion;hannan-quinn creter三个指标（越小越好））确定拟合优度最好的。

选择拟合优度最好的ARCH检验数据

Prob=0.9844>0.05不拒绝H0， 认为没有ARCH效应。

自此检验完成，可确定自回归模型函数关系：

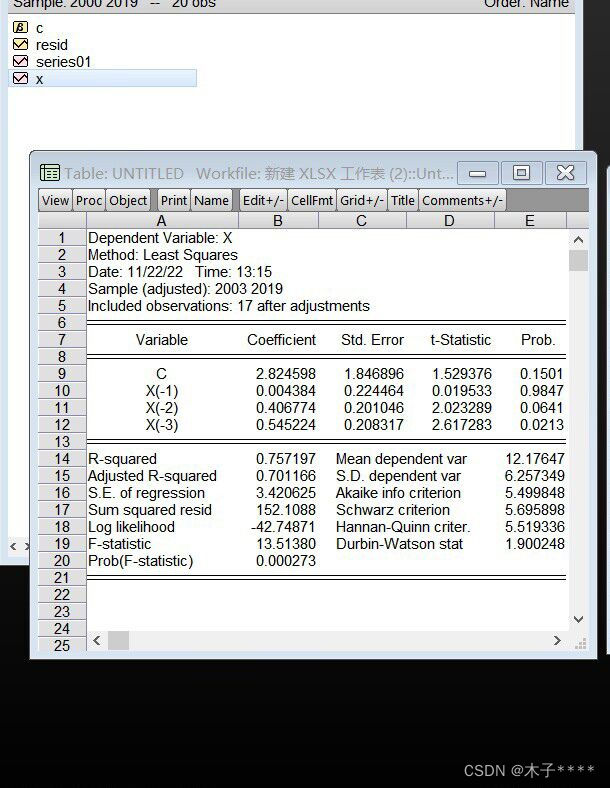
yt=0.004384yt-1 + 0.406774yt-2 + 0.545224yt-3+2.824598 +误差项

计量经济学笔记4-Eviews操作-可线性化模型与虚拟变量

目录

• 非线性方程
• 单个时间序列
• 虚拟变量
• 多个虚拟变量

非线性方程

对于非线性方程，例如

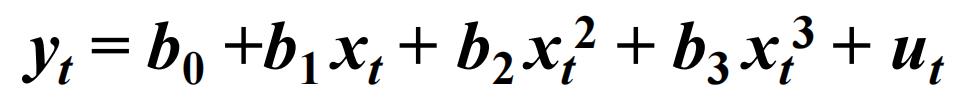
只需要在输入方程的时候体现就行

可以在view中查看具体的方程表达式


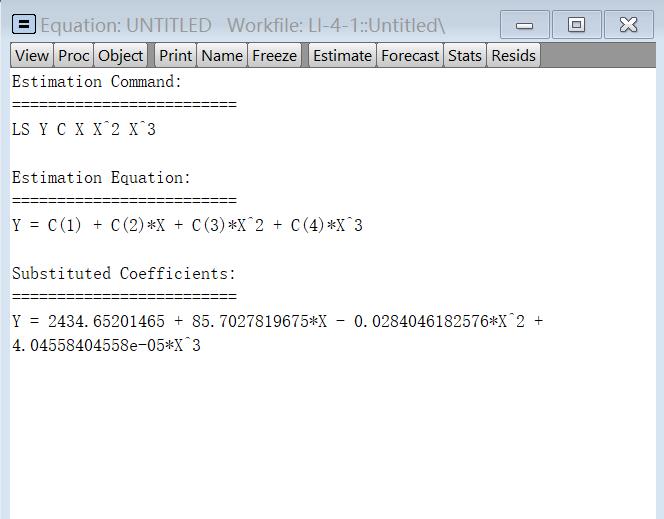
当不确定方程应该是什么形式时
可以先拟合一个线性方程，然后预测并画图

三个变量一起画图时，第一个变量是横轴，其余的都是纵轴
选择散点图scatter
将拟合值的样式改为线条

结果如下

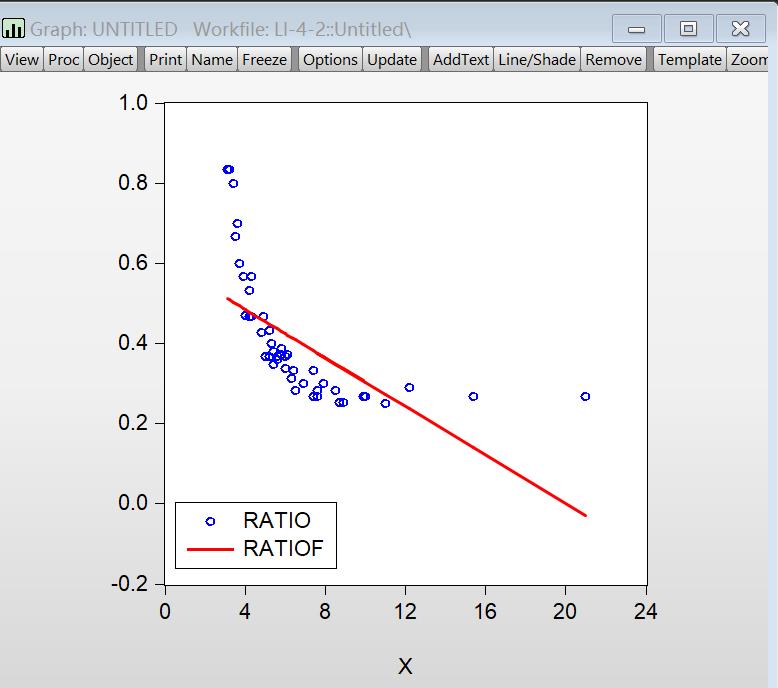
显然这里用线性关系是不准确的
因此考虑用双曲线重新拟合模型

单个时间序列

对于单个时间序列，例如研究1980-2017年GDP增长趋势
只有GDP的数据，要拟合对数线性模型log(GDP)
可以将方程写为

其中@trend(1979)表示从1980年开始为1的序列
可以新建一个序列来查看一下

定义一个time

查看time

如果想让1980年的值就是1980
可以在这个序列的基础上加上1979

虚拟变量

d1是0-1变量

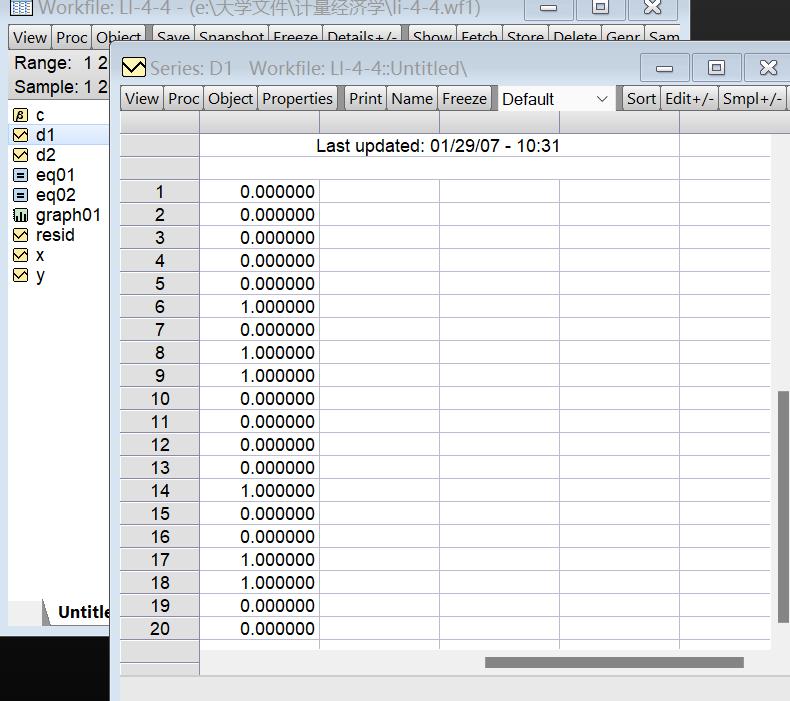
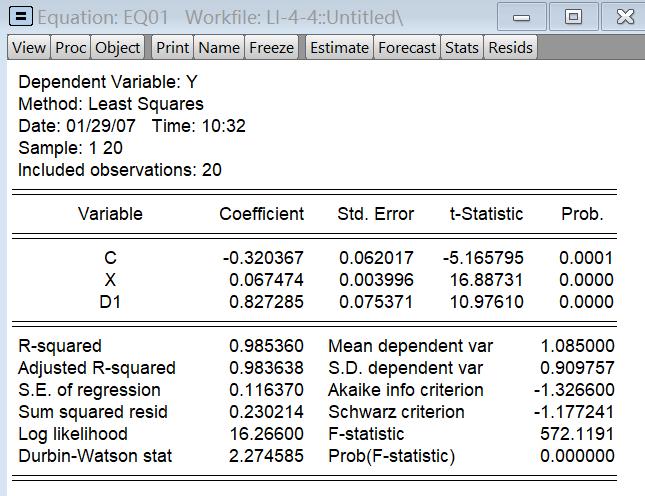
将d1加入模型


发现d1*x不显著，因此将这一项剔除

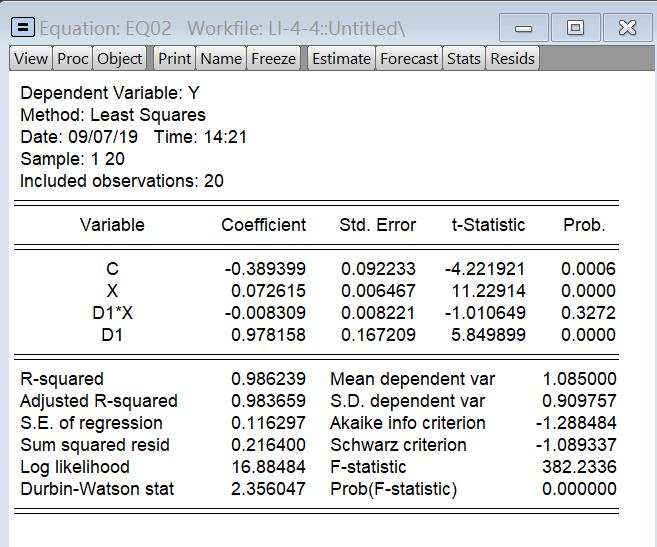
重新拟合模型

多个虚拟变量

假如要对四个季节各设一个虚拟变量

首先点击range一行，设置structure里面的起始年份

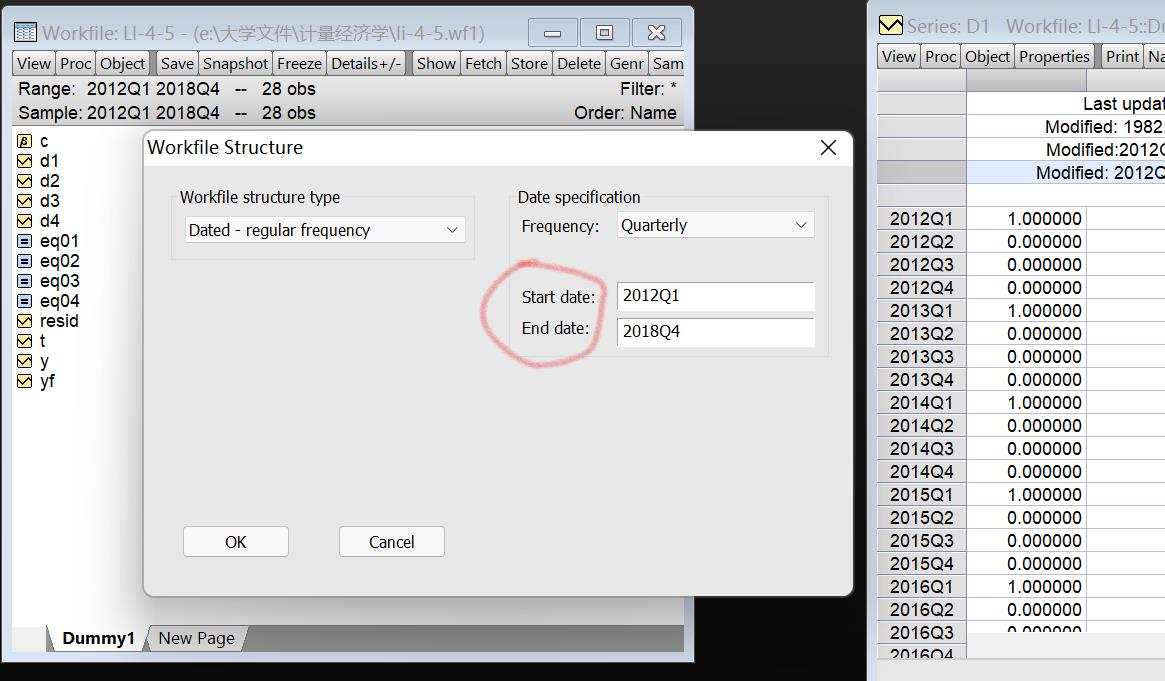
表示从2012年第一季度到2018年第四季度
然后是创建4个虚拟变量
以d1为例
先建一个空白的series
在proc里面用公式创建序列


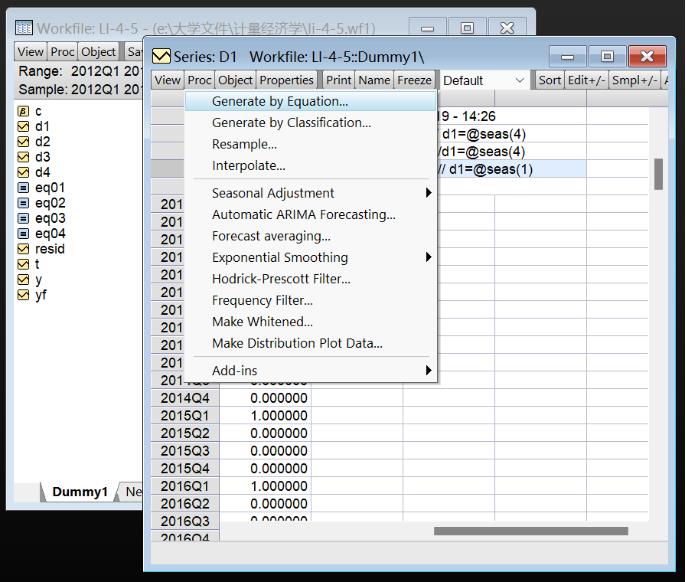
这个序列就是第一季度为1，其他季度为0的虚拟变量
设虚拟变量只改变截距，不改变斜率
则模型表示为

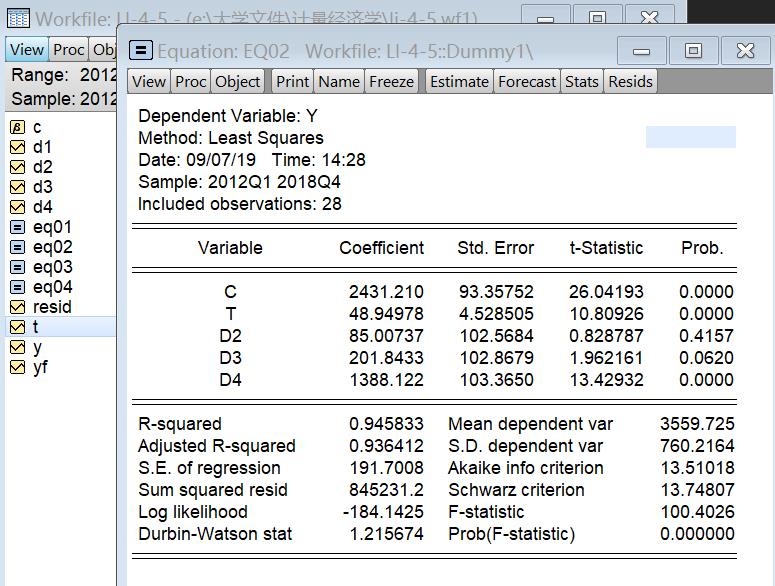
其中T为从1开始的序列
发现D2和D3均不显著
也可以设虚拟变量能改变斜率
发现不显著

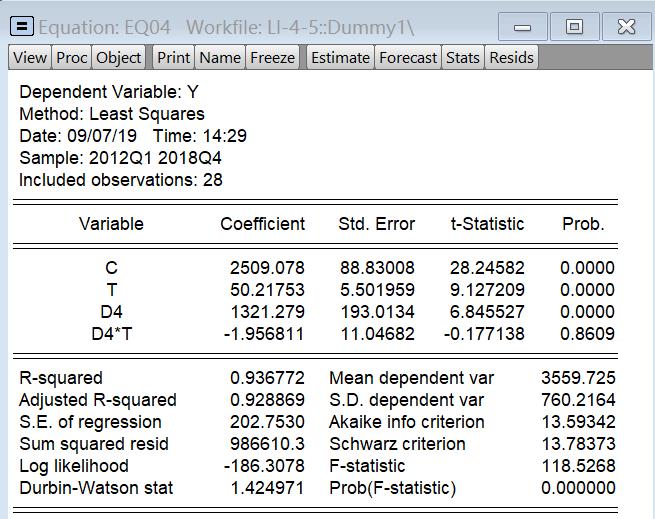
当定性变量含有m个类别时，模型不能引入m个虚拟变量。最多只能引
入m -1个虚拟变量，否则当模型中存在截距项时就会产生完全多重共线性，无法估计回归参数。称为虚拟变量陷阱。