C#,码海拾贝(03)——积分Integral算法类,《C#数值计算算法编程》源代码升级改进版
Posted 深度混淆
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C#,码海拾贝(03)——积分Integral算法类,《C#数值计算算法编程》源代码升级改进版相关的知识,希望对你有一定的参考价值。

一、引言
1.1 图书简介
《C#数值计算——算法编程》是2007年1月1日电子工业出版社出版的图书,由周长发编写。
ISBN:9787121032035
本书囊括了近90个实用经典算法,每一个算法都独立成节。每一节都包括算法原理、算法实现和示例3个部分。算法原理部分分别讨论每一种算法的计算原理;算法实现部分讨论用C#实现算法的技巧,针对不同的算法设计了6个算法类,给出完整的类和算法函数的源程序;示例部分介绍算法类的调用方式,给出调用算法的示例源程序、验证算法的示例数据和运算结果。本书内容丰富,讲解细致,实例丰富,适合涉及科学与工程数值计算工作的科研人员、工程技术人员、管理人员,以及大专院校相关专业的师生参考阅读。
作者虽然出了不少书,写了不少各种语言的代码,但都是实验室产品,无法适用于商业化、工业化场景,做一些修正才基本能用。
1.2 积分算法目录
数值计算是 周长发 老师《C#数值计算算法编程》的第7章的内容。
第7章 数值积分
7.1 数值积分类设计
7.2 变步长梯形求枳法
7.3 变步长辛卜生求积法
7.4 自适应梯形求积法
7.5 龙贝格求积法
7.6 计算—维积分的连分式法
7.7 高振荡函数求枳法
7.8 勒让德—高斯求积法
7.9 拉盖尔—高斯求积法
7.10 埃尔米特—高斯求积法
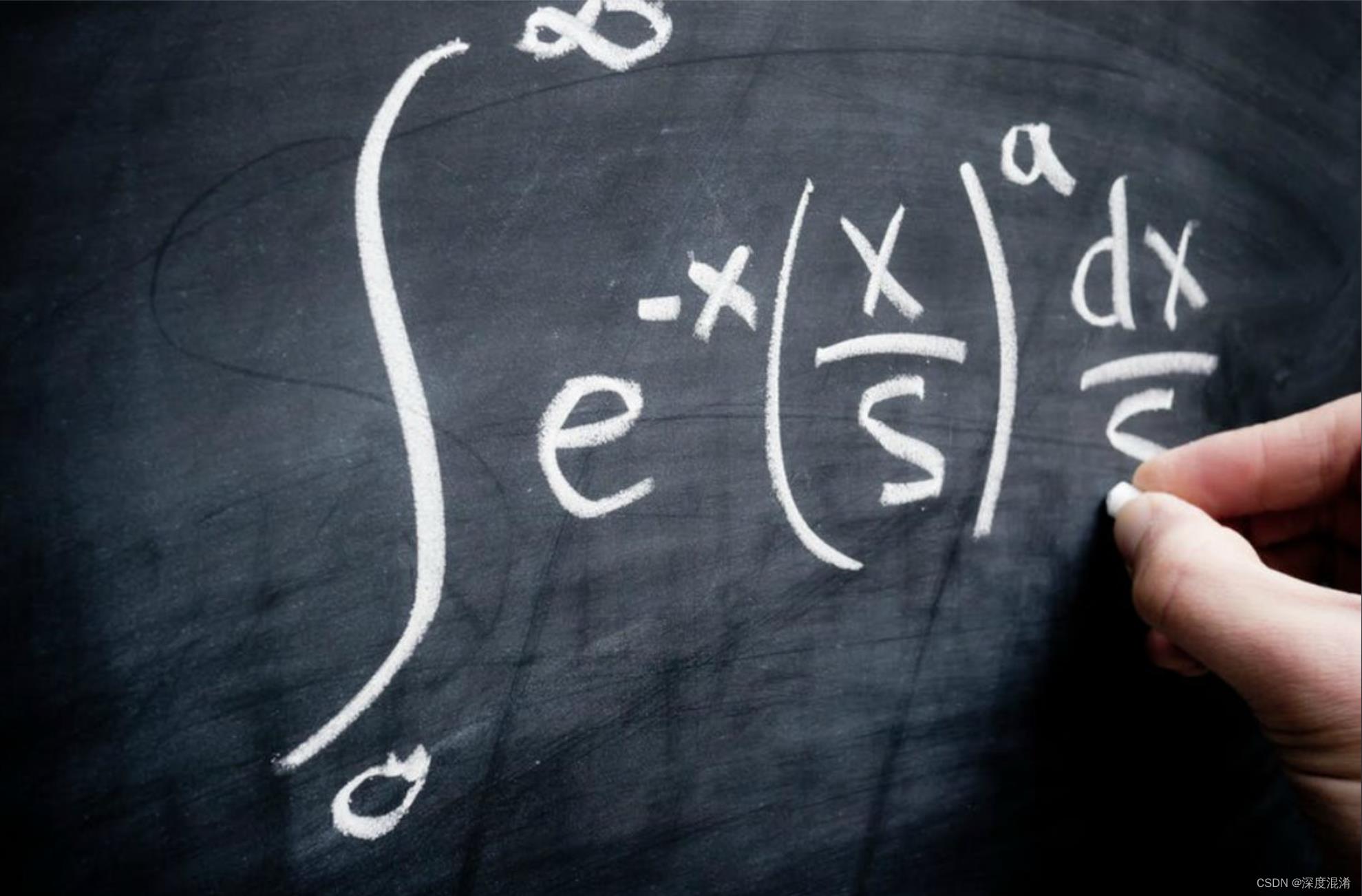
本文发布的代码是其中源代码的改进升级版。
二、改进升级版本的代码
2.1 改进要点
(1)符合最新的C#语法要求;
(2)符合数值计算的特色;
(3)符合C#语言的编程习惯;
(4)使用委托 delegate ,而不是虚函数 virtual function;
(5)使用静态类static class,而不是普通的类;
2.2 改进升级版本的C#源代码
using System;
namespace Zhou.CSharp.Algorithm
/// <summary>
/// 委托函数
/// 定义了被积分的函数(表达式)
/// </summary>
/// <param name="x"></param>
/// <returns></returns>
public delegate double IntegrableFunction(double x);
/// <summary>
/// 计算数值积分的类 Integral.cs
/// 调用前需定义委托函数 func
/// 作者:周长发
/// 改编:深度混淆
/// https://blog.csdn.net/beijinghorn
/// </summary>
public static class Integral
/// <summary>
/// 委托函数
/// 积分计算之前需要给定该委托,比如:
/// double function_name(double x) return x * x;
/// Integral.func = function_name;
/// </summary>
public static IntegrableFunction func = null;
/// <summary>
/// 变步长梯形求积法
/// </summary>
/// <param name="left">积分下限</param>
/// <param name="right">积分上限,要求 right 大于 left</param>
/// <param name="eps">积分精度要求</param>
/// <returns>积分值</returns>
public static double Trapezoidal(double left, double right, double eps = 1.0E-7)
if (right <= left)
return 0.0;
// 积分区间端点的函数值
double fa = func(left);
double fb = func(right);
// 迭代初值
int n = 1;
double h = right - left;
double t1 = h * (fa + fb) / 2.0;
double p = eps + 1.0;
// 迭代计算
double t = 0.0;
while (p >= eps)
double s = 0.0;
for (int k = 0; k < n; k++)
double x = left + (k + 0.5) * h;
s += func(x);
t = (t1 + h * s) / 2.0;
p = Math.Abs(t1 - t);
t1 = t;
n += n;
h /= 2.0;
return (t);
/// <summary>
/// 变步长辛卜生求积法
/// </summary>
/// <param name="left">积分下限</param>
/// <param name="right">积分上限,要求 right 大于 left</param>
/// <param name="eps">积分精度要求</param>
/// <returns>积分值</returns>
public static double Simpson(double left, double right, double eps = 1.0E-7)
if (right <= left)
return 0.0;
// 计算初值
int n = 1;
double h = right - left;
double t1 = h * (func(left) + func(right)) / 2.0;
double s1 = t1;
double ep = eps + 1.0;
// 迭代计算
double s2 = 0.0;
while (ep >= eps)
double p = 0.0;
for (int k = 0; k < n; k++)
double x = left + (k + 0.5) * h;
p += func(x);
double t2 = (t1 + h * p) / 2.0;
s2 = (4.0 * t2 - t1) / 3.0;
ep = Math.Abs(s2 - s1);
t1 = t2;
s1 = s2;
n += n;
h /= 2.0;
return (s2);
/// <summary>
/// 自适应梯形求积法
/// </summary>
/// <param name="left">积分下限</param>
/// <param name="right">积分上限,要求 right 大于 left</param>
/// <param name="step">对积分区间进行分割的最小步长,当子区间的宽度
/// 小于d时,即使没有满足精度要求,也不再往下进行分割</param>
/// <param name="eps">积分精度要求</param>
/// <returns>积分值</returns>
public static double Adaptive_Trapezoidal(double left, double right, double step, double eps = 1.0E-7)
if (right <= left)
return 0.0;
// 迭代初值
double h = right - left;
double f0 = func(left);
double f1 = func(right);
double t0 = h * (f0 + f1) / 2.0;
double[] t = new double[2] 0.0, 0.0 ;
// 递归计算
ppp(left, right, h, f0, f1, t0, eps, step, ref t);
double z = t[0];
return (z);
/// <summary>
/// 内部函数
/// </summary>
/// <param name="x0"></param>
/// <param name="x1"></param>
/// <param name="h"></param>
/// <param name="f0"></param>
/// <param name="f1"></param>
/// <param name="t0"></param>
/// <param name="eps"></param>
/// <param name="d"></param>
/// <param name="t"></param>
private static void ppp(double x0, double x1, double h, double f0, double f1, double t0, double eps, double d, ref double[] t)
double x = x0 + h / 2.0;
double f = func(x);
double t1 = h * (f0 + f) / 4.0;
double t2 = h * (f + f1) / 4.0;
double p = Math.Abs(t0 - (t1 + t2));
if ((p < eps) || (h / 2.0 < d))
t[0] = t[0] + (t1 + t2);
return;
else
double g = h / 2.0;
double eps1 = eps / 1.4;
// 递归
ppp(x0, x, g, f0, f, t1, eps1, d, ref t);
ppp(x, x1, g, f, f1, t2, eps1, d, ref t);
return;
/// <summary>
/// 龙贝格求积法
/// </summary>
/// <param name="left">积分下限</param>
/// <param name="right">积分上限,要求 right 大于 left</param>
/// <param name="eps">积分精度要求</param>
/// <returns>积分值</returns>
public static double Romberg(double left, double right, double eps = 1.0E-7)
if (right <= left)
return 0.0;
// 迭代初值
int m = 1;
int n = 1;
double h = right - left;
double ep = eps + 1.0;
const int steps = 10;
double[] y = new double[steps];
y[0] = h * (func(left) + func(right)) / 2.0;
// 迭代计算
double g = 0.0;
while ((ep >= eps) && (m < steps))
double p = 0.0;
for (int i = 0; i < n; i++)
double x = left + (i + 0.5) * h;
p += func(x);
p = (y[0] + h * p) / 2.0;
double s = 1.0;
for (int k = 0; k < m; k++)
s = 4.0 * s;
g = (s * p - y[k]) / (s - 1.0);
y[k] = p;
p = g;
ep = Math.Abs(g - y[m - 1]);
m++;
y[m - 1] = g;
n += n;
h /= 2.0;
return (g);
/// <summary>
/// 计算一维积分的连分式法
/// </summary>
/// <param name="left">积分下限</param>
/// <param name="right">积分上限,要求 right 大于 left</param>
/// <param name="eps">积分精度要求</param>
/// <returns>积分值</returns>
public static double Continued_Fraction(double left, double right, double eps = 1.0E-7)
if (right <= left)
return 0.0;
// 迭代初值
int m = 1;
int n = 1;
double hh = right - left;
double t1 = hh * (func(left) + func(right)) / 2.0;
double s1 = t1;
double ep = 1.0 + eps;
const int steps = 10;
double[] h = new double[steps];
h[0] = hh;
double[] bb = new double[steps];
bb[0] = s1;
// 迭代计算
double g = 0.0;
while ((ep >= eps) && (m < steps))
double s = 0.0;
for (int k = 0; k < n; k++)
double x = left + (k + 0.5) * hh;
s += func(x);
double t2 = (t1 + hh * s) / 2.0;
m++;
h[m - 1] = h[m - 2] / 2.0;
g = t2;
int w = 0;
int j = 2;
while ((w == 0) && (j <= m))
s = g - bb[j - 2];
if (Math.Abs(s) < float.Epsilon)
w = 1;
else
g = (h[m - 1] - h[j - 2]) / s;
j++;
bb[m - 1] = g;
if (w != 0)
bb[m - 1] = float.MaxValue;
g = bb[m - 1];
for (j = m; j > 1; j--)
g = bb[j - 2] - h[j - 2] / g;
ep = Math.Abs(g - s1);
s1 = g;
t1 = t2;
hh /= 2.0;
n += n;
return (g);
/// <summary>
/// 高振荡函数求积法
/// </summary>
/// <param name="left">积分下限</param>
/// <param name="right">积分上限,要求 right 大于 left</param>
/// <param name="m">被积函数中振荡函数的角频率</param>
/// <param name="n">给定积分区间两端点上的导数最高阶数+1/param>
/// <param name="fa">一维数组,长度为n,存放f(x)在积分区间端点x=a处的各阶导数值</param>
/// <param name="fb">一维数组,长度为n,存放f(x)在积分区间端点x=b处的各阶导数值</param>
/// <param name="s">一维数组,长度为2,其中s(1)返回f(x)cos(mx)在积分区间的积分值,s(2) 返回f(x)sin(mx)在积分区间的积分值</param>
/// <returns></returns>
public static double High_Oscillation(double left, double right, int m, int n, double[] fa, double[] fb, out double[] s)
// 三角函数值
double sma = Math.Sin(m * left);
double smb = Math.Sin(m * right);
double cma = Math.Cos(m * left);
double cmb = Math.Cos(m * right);
#if __OLD__
// 迭代初值
sa[0] = sma;
sa[1] = cma;
sa[2] = -sma;
sa[3] = -cma;
sb[0] = smb;
sb[1] = cmb;
sb[2] = -smb;
sb[3] = -cmb;
ca[0] = cma;
ca[1] = -sma;
ca[2] = -cma;
ca[3] = sma;
cb[0] = cmb;
cb[1] = -smb;
cb[2] = -cmb;
cb[3] = smb;
s[0] = 0.0;
s[1] = 0.0;
#else
s = new double[2] 0.0, 0.0 ;
if (right <= left)
return 0.0;
double[] sa = new double[4] sma, cma, -sma, -cma ;
double[] sb = new double[4] smb, cmb, -smb, -cmb ;
double[] ca = new double[4] cma, -sma, -cma, sma ;
double[] cb = new double[4] cmb, -smb, -cmb, -smb ;
#endif
// 循环迭代
int mm = 1;
for (int k = 0; k < n; k++)
int j = k;
while (j >= 4)
j -= 4;
mm *= m;
s[0] = s[0] + (fb[k] * sb[j] - fa[k] * sa[j]) / (1.0 * mm);
s[1] = s[1] + (fb[k] * cb[j] - fa[k] * ca[j]) / (1.0 * mm);
s[1] = -s[1];
return s[0];
/// <summary>
/// 勒让德-高斯求积法
/// </summary>
/// <param name="left">积分下限</param>
/// <param name="right">积分上限,要求 right 大于 left</param>
/// <param name="eps">积分精度要求</param>
/// <returns>积分值</returns>
public static double Legendre_Gauss(double left, double right, double eps = 1.0E-7)
if (right <= left)
return 0.0;
// 勒让德-高斯求积系数
double[] t = new double[5] -0.9061798459, -0.5384693101, 0.0, 0.5384693101, 0.9061798459 ;
double[] c = new double[5] 0.2369268851, 0.4786286705, 0.5688888889, 0.4786286705, 0.2369268851 ;
// 迭代初值
int m = 1;
double h = right - left;
double s = Math.Abs(0.001 * h);
double p = float.MaxValue;// 1.0e+35;
double ep = eps + 1.0;
// 迭代计算
double g = 0.0;
while ((ep >= eps) && (Math.Abs(h) > s))
g = 0.0;
for (int i = 1; i <= m; i++)
double aa = left + (i - 1.0) * h;
double bb = left + i * h;
double w = 0.0;
for (int j = 0; j < 5; j++)
double x = ((bb - aa) * t[j] + (bb + aa)) / 2.0;
w += func(x) * c[j];
g += w;
g = g * h / 2.0;
ep = Math.Abs(g - p) / (1.0 + Math.Abs(g));
p = g;
m++;
h = (right - left) / m;
return (g);
/// <summary>
/// 拉盖尔-高斯求积法
/// </summary>
/// <returns></returns>
public static double Laguerre_Gauss()
// 拉盖尔-高斯求积系数
double[] t = new double[5] 0.26355990, 1.41340290, 3.59642600, 7.08580990, 12.64080000 ;
double[] c = new double[5] 0.6790941054, 1.638487956, 2.769426772, 4.315944000, 7.104896230 ;
// 循环计算
double g = 0.0;
for (int i = 0; i < 5; i++)
double x = t[i];
g += c[i] * func(x);
return (g);
/// <summary>
/// 埃尔米特-高斯求积法
/// </summary>
/// <returns></returns>
public static double Hermite_Gauss()
// 埃尔米特-高斯求积系数
double[] t = new double[5] -2.02018200, -0.95857190, 0.0, 0.95857190, 2.02018200 ;
double[] c = new double[5] 1.181469599, 0.9865791417, 0.9453089237, 0.9865791417, 1.181469599 ;
// 循环计算
double g = 0.0;
for (int i = 0; i < 5; i++)
double x = t[i];
g += c[i] * func(x);
return (g);
POWER BY 315SOFT.COM

POWER BY TRUFFER.CN
scipy积分 integral
#!/usr/bin/env python # -*- coding: utf-8 -*- # @Time : 2018/5/24 15:03 # @Author : zhang chao # @File : s.py #integral积分 import numpy as np from scipy.integrate import quad,dblquad,nquad print(quad(lambda x:np.exp(-x),0,np.inf))#lambda x:np.exp(-x)定义函数,它的积分;定义区间为0-inf #结果为(1.0000000000000002, 5.842606703608969e-11) #1.0000000000000002为积分的值;5.842606703608969e-11为误差的范围 print(dblquad(lambda t,x:np.exp(-x*t)/t**3,0,np.inf,lambda x:1,lambda x:np.inf)) #dblquad为二元积分,lambda t,x:np.exp(-x*t)/t**3为积分函数;0,np.inf为t的取值范围; #lambda x:1,lambda x:np.inf其实为x的取值范围,定义为t的函数 #结果为(0.33333333325010883, 1.3888461883425516e-08) #nquad为多维积分,多元积分 def f(x,y): return x*y def bound_y(): return [0,0.5] def bound_x(y): return [0,1-2*y] print(nquad(f,[bound_x,bound_y]))#(0.010416666666666668, 4.101620128472366e-16)
以上是关于C#,码海拾贝(03)——积分Integral算法类,《C#数值计算算法编程》源代码升级改进版的主要内容,如果未能解决你的问题,请参考以下文章