机器学习中的数学原理——过拟合正则化与惩罚函数

Posted 2023-03-31 爱睡觉的咋

通过这篇博客，你将清晰的明白什么是过拟合、正则化、惩罚函数。这个专栏名为白话机器学习中数学学习笔记，主要是用来分享一下我在 机器学习中的学习笔记及一些感悟，也希望对你的学习有帮助哦！感兴趣的小伙伴欢迎私信或者评论区留言！这一篇就更新一下《 白话机器学习中的数学——过拟合、正则化与惩罚函数》

文章目录

• 一、过拟合
• 二、正则化
• • 2.1 正则化的方法
  • 2.2 正则化的效果
• 三、惩罚函数

一、过拟合

之前我们提到过的模型只能拟合训练数据的状态被称为过拟合，英文是 overfitting。记得在学习回归的时候，过度增加函数 fθ(x)的次数会导致过拟合。过拟合不止在回归时出现，在分类时也经常发生，我们要时常留意它。
避免过拟合有以下方法：

• 增加全部训练数据的数量
• 使用简单的模型
• 正则化

首先，重要的是增加全部训练数据的数量。之前我也讲过，机器学习是从数据中学习的，所以数据最重要。另外，使用更简单的模型也有助于防止过拟合。

二、正则化

2.1 正则化的方法

还记得我们在讲解回归的时候提到的目标函数吗？

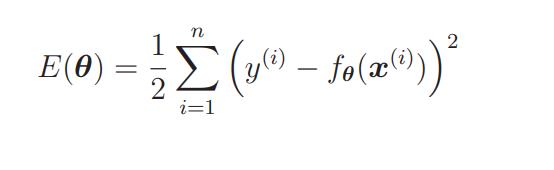
我们要向这个目标函数增加下面这样的正则化项：

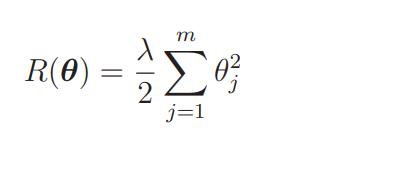
那么现在的$E(\mathbf{\theta })$就变为：

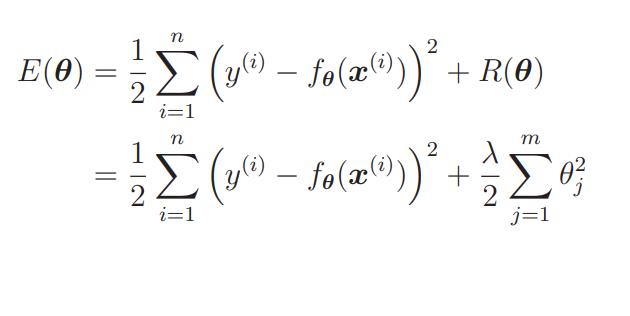
我们要对这个新的目标函数进行最小化，这种方法就称为正则化。
m 是参数的个数，不过一般来说不对 θ0 应用正则化。所以仔细看会发现 j 的取值是从 1 开始的。也就是说，假如预测函数的表达式为 fθ(x) = θ0 + θ1x + θ2x2，那么 m = 2 就意味着正则化的对象参数为 θ1 和 θ2，θ0 这种只有参数的项称为偏置项，一般不对它进行正则化。λ 是决定正则化项影响程度的正的常数。这个值需要我们自己来定。

2.2 正则化的效果

光看表达式可能不容易理解。我们结合图来想象一下吧:首先把目标函数分成两个部分。

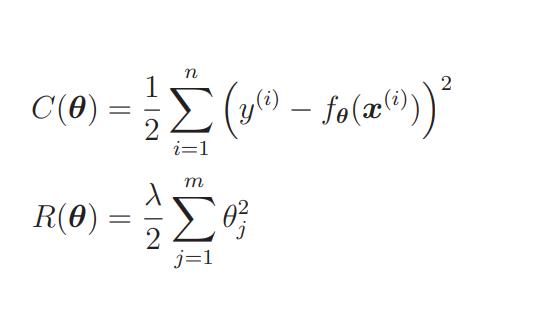
C(θ) 是本来就有的目标函数项，R(θ) 是正则化项。 C(θ) 和 R(θ) 相加之后就是新的目标函数，所以我们实际地把这两个函数的图形画出来，加起来看看。不过参数太多就画不出图来了，所以这里我们只关注 θ1。而且为了更加易懂，先不考虑 λ。
我们先从C(θ) 开始画起，不用太在意形状是否精确。在讲回归的时候，我们说过这个目
标函数开口向上，还记得吗？所以，我们假设它的形状是这样的：

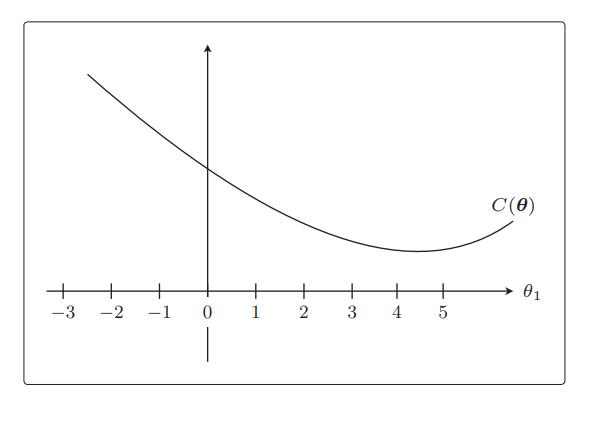
从图中马上就可以看出最小值在哪里，是在θ1 = 4.5 附近。

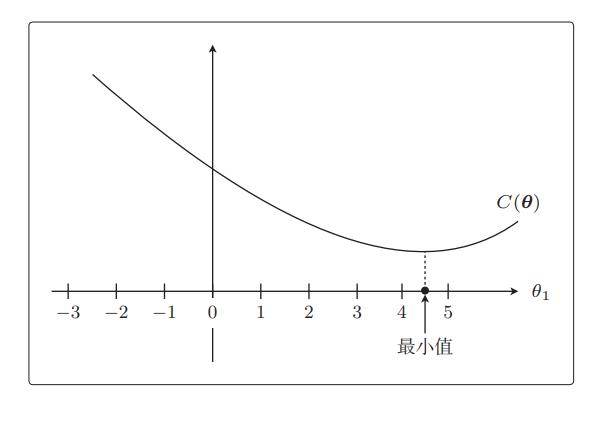
从这个目标函数在没有正则化项时的形状来看，θ1 = 4.5 附近是最小值。接下来是 R(θ)，它就相当于$\frac{1}{2}{\theta }_1^2$所以是过原点的简单二次函数。

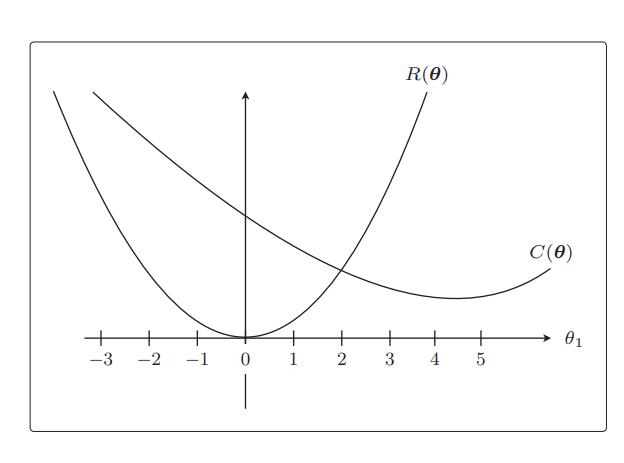
实际的目标函数是这两个函数之和E(θ) = C(θ) + R(θ)，我们来画一下它的图形。顺便考虑一下最小值在哪里。把 θ1 各点上的 C(θ) 和 R(θ) 的高相加，然后用线把它们相连就好：

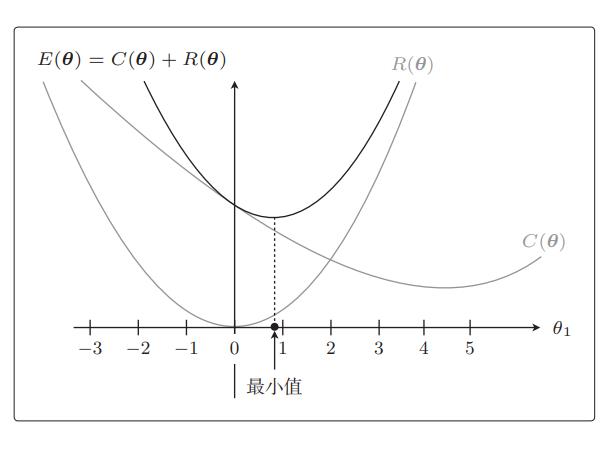
从图中我们可以看出来最小值是 θ1 = 0.9，与加正则化项之前相比，θ1 更接近 0 了。本来是在 θ1 = 4.5 处最小，现在是在 θ1 = 0.9 处最小，的确更接近 0 了。这就是正则化的效果。它可以防止参数变得过大，有助于参数接近较小的值。虽然我们只考虑了 θ1，但其他 θj 参数的情况也是类似的。
参数的值变小，意味着该参数的影响也会相应地变小。比如，有这样的一个预测函数 fθ(x):$$f_{\mathbf{\theta }}(\mathbf{x})={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2$$
极端一点，假设 θ2 = 0，这个表达式就从二次变为一次了，这就意味着本来是曲线的预测函数变为直线了：

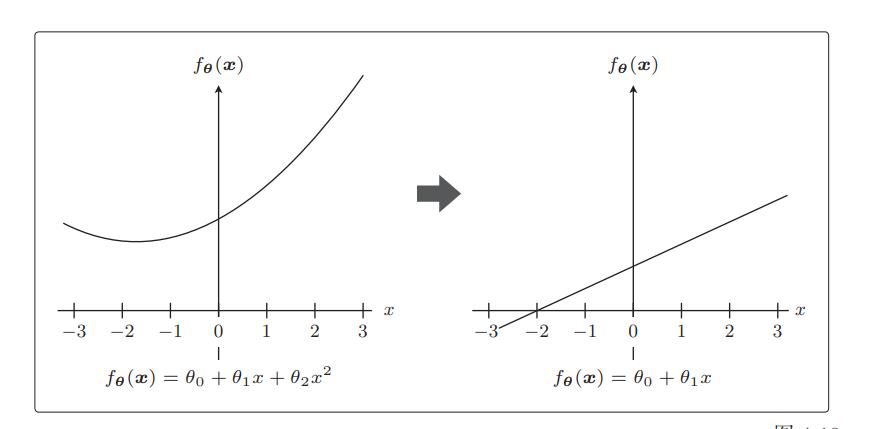
这正是通过减小不需要的参数的影响，将复杂模型替换为简单模型来防止过拟合的方式。

三、惩罚函数

为了防止参数的影响过大，在训练时要对参数施加一些惩罚。比如上面提到的 λ，可以控制正则化惩罚的强度。$$\begin{array}{rl}& C(\mathbf{\theta })=\frac{1}{2}\sum _{i=1}^n{\left(y^{(i)}-f_{\mathbf{\theta }}\left({\mathbf{x}}^{(i)}\right)\right)}^2\\ & R(\mathbf{\theta })=\frac{\lambda }{2}\sum _{j=1}^m{\theta }_j^2\end{array}$$
比如令 λ = 0，那就相当于不使用正则化

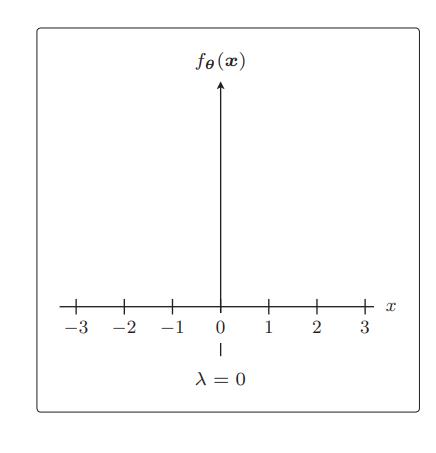
λ 越大，正则化的惩罚也就越严厉：

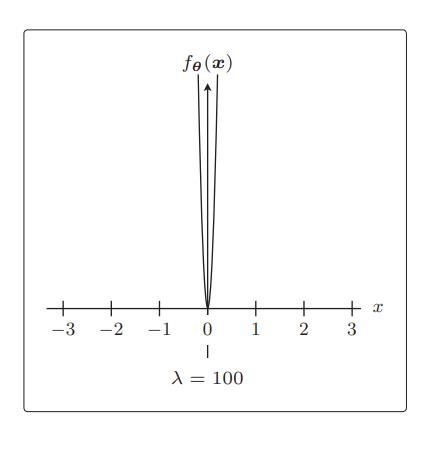
机器学习之路： python线性回归 过拟合 L1与L2正则化

git：https://github.com/linyi0604/MachineLearning

正则化：
    提高模型在未知数据上的泛化能力
    避免参数过拟合
正则化常用的方法：
    在目标函数上增加对参数的惩罚项
    削减某一参数对结果的影响力度

L1正则化：lasso
    在线性回归的目标函数后面加上L1范数向量惩罚项。
    
    f = w * x^n + b + k * ||w||1 
    
    x为输入的样本特征
    w为学习到的每个特征的参数
    n为次数
    b为偏置、截距
    ||w||1 为 特征参数的L1范数，作为惩罚向量
    k 为惩罚的力度

L2范数正则化：ridge
    在线性回归的目标函数后面加上L2范数向量惩罚项。
    
    f = w * x^n + b + k * ||w||2 
    
    x为输入的样本特征
    w为学习到的每个特征的参数
    n为次数
    b为偏置、截距
    ||w||2 为 特征参数的L2范数，作为惩罚向量
    k 为惩罚的力度
        
        
下面模拟 根据蛋糕的直径大小 预测蛋糕价格
采用了4次线性模型，是一个过拟合的模型
分别使用两个正则化方法 进行学习和预测

 1 from sklearn.linear_model import LinearRegression, Lasso, Ridge
 2 # 导入多项式特征生成器
 3 from sklearn.preprocessing import PolynomialFeatures
 4 
 5 
 6 ‘‘‘
 7 正则化：
 8     提高模型在未知数据上的泛化能力
 9     避免参数过拟合
10 正则化常用的方法：
11     在目标函数上增加对参数的惩罚项
12     削减某一参数对结果的影响力度
13 
14 L1正则化：lasso
15     在线性回归的目标函数后面加上L1范数向量惩罚项。
16     
17     f = w * x^n + b + k * ||w||1 
18     
19     x为输入的样本特征
20     w为学习到的每个特征的参数
21     n为次数
22     b为偏置、截距
23     ||w||1 为 特征参数的L1范数，作为惩罚向量
24     k 为惩罚的力度
25 
26 L2范数正则化：ridge
27     在线性回归的目标函数后面加上L2范数向量惩罚项。
28     
29     f = w * x^n + b + k * ||w||2 
30     
31     x为输入的样本特征
32     w为学习到的每个特征的参数
33     n为次数
34     b为偏置、截距
35     ||w||2 为 特征参数的L2范数，作为惩罚向量
36     k 为惩罚的力度
37         
38         
39 下面模拟 根据蛋糕的直径大小 预测蛋糕价格
40 采用了4次线性模型，是一个过拟合的模型
41 分别使用两个正则化方法 进行学习和预测
42 
43 ‘‘‘
44 
45 # 样本的训练数据，特征和目标值
46 x_train = [[6], [8], [10], [14], [18]]
47 y_train = [[7], [9], [13], [17.5], [18]]
48 # 准备测试数据
49 x_test = [[6], [8], [11], [16]]
50 y_test = [[8], [12], [15], [18]]
51 # 进行四次线性回归模型拟合
52 poly4 = PolynomialFeatures(degree=4)  # 4次多项式特征生成器
53 x_train_poly4 = poly4.fit_transform(x_train)
54 # 建立模型预测
55 regressor_poly4 = LinearRegression()
56 regressor_poly4.fit(x_train_poly4, y_train)
57 x_test_poly4 = poly4.transform(x_test)
58 print("四次线性模型预测得分:", regressor_poly4.score(x_test_poly4, y_test))  # 0.8095880795746723
59 
60 # 采用L1范数正则化线性模型进行学习和预测
61 lasso_poly4 = Lasso()
62 lasso_poly4.fit(x_train_poly4, y_train)
63 print("L1正则化的预测得分为：", lasso_poly4.score(x_test_poly4, y_test))  # 0.8388926873604382
64 
65 # 采用L2范数正则化线性模型进行学习和预测
66 ridge_poly4 = Ridge()
67 ridge_poly4.fit(x_train_poly4, y_train)
68 print("L2正则化的预测得分为：", ridge_poly4.score(x_test_poly4, y_test))  # 0.8374201759366456

 

通过比较 经过正则化的模型 泛化能力明显的更好啦