数据结构-二叉树
Posted 下一站不是永远
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构-二叉树相关的知识,希望对你有一定的参考价值。
前言
带你图解二叉树的多种递归遍历
下面开始本节课的学习
目录
二叉树的构建
结点类型的定义
构建二叉树之间的关系
深度优先遍历
前序遍历
1.代码实现
2.图解递归
中序遍历
1.代码实现
2.图解递归
后序遍历
1.代码实现
2.图解递归
广度优先遍历
1.层序遍历
2.代码实现
面试题
C语言面试题
二叉树的构建
定义:
二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分。
特点:
每个结点最多有俩孩子(二叉树中不存在度大于2的结点)。
二叉树可以是空集合,根可以有空的左子树和空的右子树。
二叉树有左右之分,次序不能颠倒。
二叉树的性质:
1.在二叉树的第i层上至多有2^(i-1)个结点(i>1)。
2.深度为k的二叉树至多有2^k-1个结点(k>=1)。
3.对任何一颗二叉树T,如果其叶子数为n0,度为2的结点数为n2,则n0=n2+1.
4. 具有n个结点的完全二叉树的深度为(log2N)+1。

二叉树的构建:
为了实现二叉树遍历,我们需要构建一个二叉树。
结点类型的定义
链式二叉树需要有自己的节点类型,所以我们先定义一个链式二叉树的模型。
typedef char BTDataType;
typedef struct BinaryNode
BTDataType x;
struct BinaryNode* left;
struct BinaryNode* right;
BT;
构建二叉树之间的关系
BT* BuyNode(BTDataType x)
BT* new = (BT*)malloc(sizeof(BT));
if (new == NULL)
printf("malloc failed\\n");
exit(-1);
new->x = x;
new->left = NULL;
new->right = NULL;
return new;
void BinaryCreat()
BT* n1 = BuyNode(A);
BT* n2 = BuyNode(B);
BT* n3 = BuyNode(C);
BT* n4 = BuyNode(D);
BT* n5 = BuyNode(E);
BT* n6 = BuyNode(F);
n1->left = n2;
n1->right = n3;
n2->left = n4;
n3->left = n5;
n3->right = n6;

深度优先遍历
二叉树的深度优先遍历有三种:
- 前序遍历
- 中序遍历
- 后序遍历
前序遍历
定义: 前序遍历首先访问 根结点 然后 遍历 左子树,最后遍历右子树。 前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。 在遍历左、右子树时,仍然先访问 根结点 ,然后遍历左子树,最后遍历右子树。
- 前序遍历,又叫做先根遍历。
- 遍历顺序:根-->左子树-->右子树
代码实现
void BinaryPrev(BT* n1)
if (n1==NULL)
printf("NULL ");
return ;
printf("%c ", n1->x);
BinaryPrev(n1->left);
BinaryPrev(n1->right);
图解递归
前序遍历的代码比较简单,但是分析起来就相当于比较复杂。

中序遍历
定义:中序遍历(LDR)是 二叉树遍历 的一种,也叫做 中根遍历 、中序周游。 在二叉树中,中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。 中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。
- 中序遍历又叫做中根遍历。
- 遍历顺序:左子树-->根-->右子树
代码实现
void MiddleOrder(BT* n1)
if (n1 == NULL)
printf("NULL ");
return;
MiddleOrder(n1->left);
printf("%c ", n1->x);
MiddleOrder(n1->right);
图解递归
中序遍历的代码比较简单,但是分析起来就相当于比较复杂。

后序遍历
定义:后序遍历有 递归算法 和非递归算法两种。 在二叉树中,先左后右再根,即首先遍历左子树,然后遍历右子树,最后访问根结点。 后序遍历首先遍历左子树,然后遍历右子树,最后访问根结点,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。
- 后序遍历又叫后根遍历
- 遍历顺序:左子树-->右子树-->根
代码实现
void AfterOrder(BT* n1)
if (n1 == NULL)
printf("NULL ");
return;
AfterOrder(n1->left);
AfterOrder(n1->right);
printf("%c ", n1->x);
图解递归
广度优先遍历
层序遍历
层序遍历,自上而下,从左往右逐层访问树的结点的过程就是层序遍历。

- 思路(借助一个队列):
- 先把根入队列,然后开始从队头出数据。
- 出队头的数据,把它的左孩子和右孩子依次从队尾入队列(NULL不入队列)。
- 重复进行步骤2,直到队列为空为止。
代码实现
void BinaryLevelOrder(BT* n1)
Queue q;
QueueInit(&q);
if (n1!=NULL)
QueuePush(&q, n1);
while (!QueueEmpty(&q))
BT* front = QueueTop(&q);
QueuePop(&q);
printf("%c ", front->x);
// 不把NULL打印出来
//if (front->left!=NULL)
//
// QueuePush(&q, front->left);
//
//if (front->right != NULL)
//
// QueuePush(&q, front->right);
//
if (front->left != NULL)
QueuePush(&q, front->left);
else
printf("NULL ");
if (front->right != NULL)
QueuePush(&q, front->right);
else
printf("NULL ");
QueueDestory(&q);

面试题
已知一颗二叉树的中序序列和后序序列分别是BDCEAFHG和DECBHGFA,画出这颗树
(1)由后序遍历特征,根结点比在后序序列尾部,即根结点是A;
(2)由中序遍历特征,根结点必在中间,而且其左边必须全部是左子树子孙(BDCE),其右部必全部是右子树子孙(FHG);
(3)继而根据后序中的DECB子树可确定B为A的左孩子,根据HGF得出F为A的右孩子;依次类推,可以唯一确定一棵二叉树如图1所示。
但是,由一棵二叉树的先序序列和后序序列不能唯一确定一棵二叉树,因为无法确定左右子树两部分。例如,如果有先序序列AB,后序序列BA,因为无法确定B为左子树还是右子树,所以可以得到如图2所示的两棵不同的二叉树。


二叉树的后序序列为DBFEGCA中序序列为DBAFECG,求它的先序序列
(1) 由后序序列为DBFEGCA得到二叉树的根为A,由中序序列为DBAFECG得到二叉树的左子树子孙为:DB,右子树子孙为:FECG。
(2)我们先看它的左子树子孙,由后序序列为DB,中序序列为DB得到B为A的左孩子,D为B的左孩子。
(3)再看它的右子树子孙,由后序序列FEGC,中序序列FECG得到C为A的右孩子,C的左子树子孙为FE右孩子为G,又由后序序列FE,中序序列FE得到E为G的左孩子,F为G的左孩子
得到二叉树如下图:
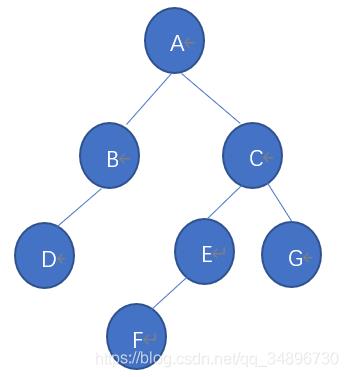
它的先序序列为:ABDCEFG


C语言面试题(11-21)
11.全局变量和局部变量在内存中是否有区别?如果有,是什么区别?
答 :全局变量储存在静态数据区,局部变量在堆栈中。
12.什么是平衡二叉树?
答 :左右子树都是平衡二叉树 且左右子树的深度差值的绝对值不大于1。
13.堆栈溢出一般是由什么原因导致的?
- 1.没有回收垃圾资源
- 2.层次太深的递归调用
14.冒泡排序算法的时间复杂度是什么?
答 :O(n^2)
15.什么函数不能声明为虚函数?
答:constructor
16、队列和栈有什么区别?
答:队列先进先出,栈后进先出
17、不能做switch()的参数类型
答 :switch的参数不能为实型。
18、局部变量能否和全局变量重名?
答:能,局部会屏蔽全局。
19.什么是预编译,何时需要预编译?
答:预编译又称为预处理,是做些代码文本的替换工作。处理#开头的指令,比如拷贝#include包含的文件代码,#define宏定义的替换,条件编译等,就是为编译做的预备工作的阶段,主要处理#开始的预编译指令,预编译指令指示了在程序正式编译前就由编译器进行的操作,可以放在程序中的任何位置。
c编译系统在对程序进行通常的编译之前,先进行预处理。c提供的预处理功能主要有以下三种:1)宏定义 2)文件包含 3)条件编译
- puts()将一个字符串输出到终端
- gets()从终端输入一个字符串到字符数组,并且得到一个函数值。
- strcat()链接两个字符数组中的字符串。
- strcpy()字符串复制函数。
- strcmp()比较字符串作用。
- strlen()测试字符串长度的函数不包括“\\0”
- strlwr()将字符串中的大写字母转换为小写字母。
- strupr()将字符串中的小写字母转换为大写字母。
20.函数
- 一个源程序由多个函数组成。
- C程序的执行从main()函数开始;
- 所有函数都是平行的;
- 函数分类;可以分为标准和自定义,还可以分为有参函数和无参函数。
21.通过指针修改内容的汇编过程
- 通过指针变量的地址,找到内容的地址
- 通过地址找到内容
- 修改内容
以上是关于数据结构-二叉树的主要内容,如果未能解决你的问题,请参考以下文章
