理解对数——金融问题中的自然对数（以e为底的对数）

Posted 2023-03-30 ComputerInBook

第3章 金融问题(Financial Matters)

——金融问题中的自然对数

If thou lend moneyto any ofMy people. ...

thou shalt not beto him as a creditor;

neither shall yelay upon him interest.

(如果你借钱给我的任何人。 ……你不应该是他的债权人；也不可向他加息。)

——EXODUS 22:24

自古以来(From timeimmemorial)，金钱问题一直是人类关注的中心。生活的其他方面没有比获得财富和实现财务安全的冲动更平凡的了(mundane)。因此，在 17 世纪早期，一位匿名数学家——或者可能是商人或放债人——注意到货币增长的方式与某个数学表达式在无穷大时的行为之间存在一种奇怪的联系，这一定是令人惊讶的。

对金钱的任何考虑的概念的核心是利息(interest)，或贷款支付的额外的钱。借钱收费的做法可以追溯到有文字记载的历史之初。 事实上，我们所知的许多最早的数学文献都涉及与利率相关的问题。例如，一块来自美索不达米亚(Mesopotamia)(古希腊对两河流域称谓)的黏土板(clay tablet)，可追溯到公元前1700 年左右,现在存放在卢浮宫(Muséedu Louvre，法国博物馆)，这块泥板提出了以下问题：如果以 20%的年复合利率投资，一笔钱需要多长时间才能翻倍？[1] 为了用代数语言来确切表达或公式化(formulate)这个问题，我们注意到每年年底总和增长 20%，即增长到原来的1.2倍；因此在x 年后总和将增长到 倍。因为问题是多久时间才能翻倍，即这等于原始总和的两倍，所以我们有 (注意原始总和不进入等式)。

现在，我们来解这个方程，即，我们必须求得这个未知的指数——我们必须使用对数，这是巴比伦人(Babylonians)所没有的方法。无论如何，他们通过观察(译注：通过直接自乘法可得)，可以求得这个指数的近似解；他们观察到， ，而 ; 因此，x 一定是一个位于区间 3 到 4 之间的数(译注：小数)。为了缩窄这个待求值的所在区间，他们使用了一个称为线性插值(interpolation)的过程。求得一个将区间 3 到 4 划分开的数，使其划分比率与2 划分区间 1.728 到2.0736 相同。这就导致产生了一个以 x 为未知量的(一阶)线性方程，这个方程可以很容易地使用初等代数知识求解。但是，巴比伦人还没有我们现代的代数技巧，对于他们来说，要求得满足要求的值并不是一项简单的任务。然而，他们给出的值x = 3.7870，非常接近正确解3.8018(即，大约 3 年零 9 个月18 天)。我们应当指出，巴比伦人不使用十进制记数系统，十进制系统仅始于中古时代早期；他们采用的是60 进制(sexagesimal)记数系统，这是一种基于数60 的进制系统，满60 进位。按照60 进制的记法，卢浮宫粘土板给出的答案是3;47,13,20 ，其中，六十进制记数系统指的是 ( )，或者是一个非常接近3.7870 的数。[2]

在某种程度上，巴马伦人确实使用了某种对数表。在现存的粘土板中，某些板列出了数 1/36,1/16，9,和 16 (前两个以六十进制系统表示为 0; 1,40 和 0;3,4)的前十个幂——所有都是完全平方。由于这样的表列出了一个数的幂而不是指数，所以除了巴比伦人没有使用单一的标准底数来表示他们的幂之外，它实际上是一张反对数表。这些表似乎是为了处理涉及复利的特定问题而不是为了一般用途而编制的。[3]

我们简单考察一下这个复利是如何执行的。假设我们在支付 5% 年利息的账户中投资 100 美元(“本金(principal)”)，每年复利。一年结束时，我们的余额将为100 x 1.05 = 105美元。然后，银行会将这笔新金额视为恰好以相同利率进行再投资的新本金。因此，在第二年末，余额将为 105 x 1.05 = 110.25 美元，在第三年末余额为 110.25x 1.05=115.76 美元，依此类推。(因此，不仅本金享有年息，前面本金之上的利息也享有利息——因此称为“复利”。) 我们看到我们的余额以等比级数(geometric progression)增长，通比(或称公比)(commonratio)为 1.05。 相比之下，在支付单利(simpleinterest)的账户中，年利率仅适用于原始本金(originalprincipal)，因此每年产生的利息都相同。如果我们以 5% 的单利投资 100 美元，我们的余额每年会增加 5 美元，这时，我们的本息呈现为等差级数(arithmeticprogression) 100,105,110,115，依此类推。显然，无论利率如何，以复利投资的资金最终将比以单利投资增长得更快。

从这个例子中很容易看出一般情况下会发生什么。假设我们将 P 美元的本金投资于一个支付 r % 年复利利率的账户(在计算中我们总是将 r 表示为小数，例如，表示为0.05 而不是5% )。这意味着在第一年末我们的余额将为P (1 + r)，第二年末我们的余额将为 ，依此类推，则t 年后余额将变成 。用S 表示这个余额，我们得出公式

---------------------------------------------------(1)

这个公式几乎是所有财务计算的基础，无论它们适用于银行账户、贷款、抵押贷款(mortgages)还是年金(annuities)。有些银行计算应计利息不是一次，而是一年计算数次。例如，如果 5% 的年利率每半年复利一次，则银行将使用年利率的二分之一作为每期利率。 因此，在一年内，100 美元的本金将复利两次，每次的利率为 2.5% ；这将达到 或 105.0625 美元，如果年复合利率为 5%，则比相同本金的收益率高出约 6 美分。

在银行业，人们会发现各种各样的复利计划——每年、每半年、每季度、每周甚至每天。假设复利每年进行 n 次。对于每个“转换期(conversionperiod)”，银行使用年利率除以 n，即 。 由于在 t 年内有 (nt ) 个转换期，本金 P 将在 t 年后产生金额

---------------------------------------------------(2)

显然，方程(1)仅仅是方程(2)的一个特例——当 n = 1 时的情况。

假设年利率相同，比较给定本金在不同转换期一年后将产生的金额将很有趣。让我们以 P = 100 美元 和 r = 5% = 0.05为例加以说明。在这里，会用到手持计算器。如果计算器有求幂键(通常用符号 表示),我们可以直接用它来讲算期望的值；此外，我们必须重复乘以因式(1 + 0.05/ n)。结果如表 3.1 所示，非常令人惊讶。 正如我们所见，100 美元的本金每日复利收益率仅比年复利高13美分，比月复利或周复利高约1美分！我们把钱投资在哪个账户上几乎没有什么区别。[4]

------------表3.1 100 美元在不同转换期以5%的年利率投资一年的余额--------------

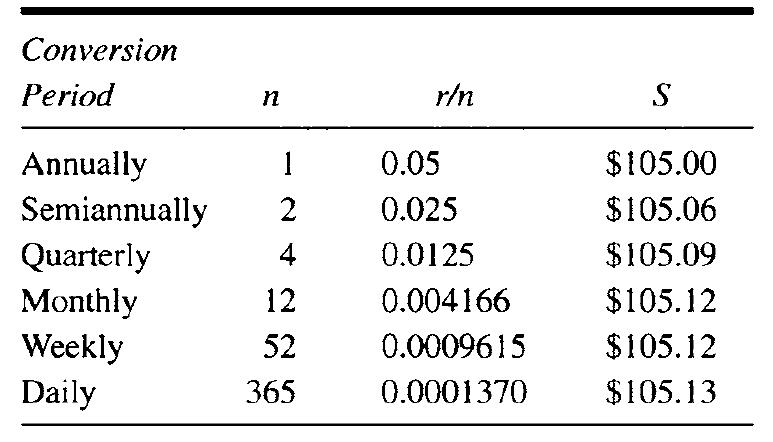
(译注：Semiannually-按半年期，quarterly-按季度)

为了进一步探讨这个问题，让我们考虑方程(2)的一个特例，即 r = 1 的情况。这意味着年利率为 100% ，而且肯定没有哪家银行提供过如此慷慨的报价。然而，我们想到的不是实际情况，而是一个具有深远数学结果的假设案例。为了简化我们的讨论，让我们假设P = 1 美元和 t = 1 年(译注：在这个表达式中，P 取多少并不影响表达式的性质，因此，为方便记，取P = 1；同时，t 的取值也不影响表达式的性质，为方便记，取 t = 1；而对于 r 的取值情况，对于某个常数来讲，当 n 趋于无穷大时， 与 呈现出来性质是一样的，因此只需分析 r = 1这种情况即可)。 方程(2)则变为

---------------------------------------------------(3)

我们的目标是研究这个公式在增加 n 值时的行为。结果在表 3.2 中给出。

--------------------表3.2 随n 变化的取值-------------------

看起来 n 的任何进一步增加都几乎不会影响结果——变化将发生在越来越不重要的数字上。

但是，这种模式会一直随着n 的增大而保持不变吗？是否有可能无论n 有多大， 的值都将稳定在 2.71828 附近？详细的数学分析确实证实了这种有趣的可能性(见附录2)。我们不知道是谁最先注意到表达式 随着 n 趋于无穷大时的特殊行为，因此后来采用e 表示这个奇特数的确切日期仍不确定。然而，它的起源似乎可以追溯到17 世纪初，大约在 Napier 发明对数的同一时期。(正如我们所见，Edward Wright对 Napier的 “对数说明书(Descriptio)”[1618] 的译本第二版间接引用了e。) 这一时期的标志是国际贸易的巨大增长，各种金融交易激增；结果，人们对复利法则给予了极大的关注，并且数e 可能在这种情况下得到了第一个认可。然而，我们很快就会看到，与复利无关的问题也几乎在同一时间导出了这个相同的数。但在我们转向研究这些问题之前，我们最好仔细看看 e 的根(root)的数学过程：极限过程。

说明与资料来源：

1. 参见 HowardEves 所著<< AnIntroduction to the History of Mathematics>>(数学简史)(1964年初版; Philadelphia: SaundersCollege Publishing, 1983重印)第36页。

2. 参见 CarlB. Boyer 所著<<A History of Mathematics>>(数学史,修订版)( NewYork: John Wiley,1989出版)第36页。

3. 同2.，第35页。

4. 当然，差额还是和本金成正比的。如果我们投资1,000,000 美元而不是100 美元，那么如果按年复利计算，我们在第一年末的余额将为1,050,000 美元，而如果按日复利计算则为1,051,267.50 美元——相差1267.50 美元。你总是有钱更好！

内容来源：

<<e:The story of a number>> (数e的故事) 作者：Eli Maor

Math对象

Math对象属性

Math.E 常量e,即自然对数的底数（约等 于2.718)。

Math.LN2 2 的 自 然 对 数 （约 等 于 0.693)。

Math.LN10 10的自然对数（约等于 2.302）。

Math.LOG2E 以2为底的e的对数（约等于1.414)。

Math.LOG10E 以10为底的e的对数（约 等于0.434）。

Math.PI 圆周率（约等于3.14159） 。

Math.SQRT1_2 2的平方根的倒数（约等 于 0.707）。

Math.SQRT2 2 的 平方根 （约等于1.414）。

Math对象方法

Math.min() 确定一组数值中的最小值，接收任意多的数值参数。

Math.max() 确定一组数值中的最大值，接收任意多的数值参数。

Math.ceil() 对数进行上舍入为最接近的整数。

Math.floor() 对数进行下舍入为最接近的整数。

Math.round() 把数四舍五入为最接近的整数。

Math.random() 返回0~1之间的随机数。

Math.abs() 返回数的绝对值。

Math.exp()  返回e的指数。

Math.sqrt() 返回数的平方根。

Math.valueOf() 返回Math对象的原始值。