python《多媒体技术与应用》实验报告「数字音频处理」
Posted Khalil三省
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了python《多媒体技术与应用》实验报告「数字音频处理」相关的知识,希望对你有一定的参考价值。
《多媒体技术与应用》实验报告
| 实验名称 | 数字视频处理 | 实验时间 | 2022/4/25 | ||||||||||||||||||||||||||||||||||
| 姓名 | 班级 | 计非201 | 学号 | 成绩 | |||||||||||||||||||||||||||||||||
| 一. 实验目的 1.掌握数字音频的读取与打开; 2.掌握数字音频信号的频谱分析; 3.验证 PCM 编码算法。 | |||||||||||||||||||||||||||||||||||||
| 二.实验原理 声音是由物体振动而产生的,声波的三要素是频率、振幅和波形,频率代表音阶的高低, 振幅代表响度(音量),波形代表音色,采样频率越高所能描述的声波频率就越高。采样率决定声音频率的范围(相当于音调),可以用数字波形表示。以波形表示的频率范围通常被称为带宽。 采样频率是单位时间内对媒体对象的采样次数,单位为赫兹 Hz。采样频率是指录音设备在一秒钟内对声音信号的采样次数,采样频率越高声音的还原就越真实越自然。脉冲编码调制(PCM,Pulse Code Modulation)在通信系统中完成将语音信号数字化功能。是一种对模拟信号数字化的取样技术,将模拟信号变换为数字信号的编码方式,特别是对于音频信号。 PCM 的实现主要包括三个步骤完成:抽样、量化、编码。分别完成时间上离散、幅度上离散、及量化信号的二进制表示。根据 CCITT 的建议,为改善小信号量化性能,采用压扩非均匀量化,有两种建议方式,分别为 A 律和 m 律方式,本设计采用了 A 律方式。 | |||||||||||||||||||||||||||||||||||||
| 三.实验内容与关键步骤 1. 打开音频信号文件,获取音高、音量等信息; 2. 对打开的文件进行频谱分析; 3. 验证 PCM 算法。 | |||||||||||||||||||||||||||||||||||||
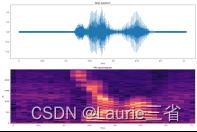
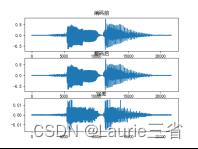
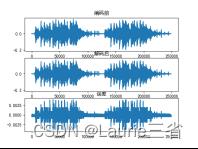
| 四.代码 4-1 音量 4-2 音高 4-3 波形频谱 4-4 PCM | |||||||||||||||||||||||||||||||||||||
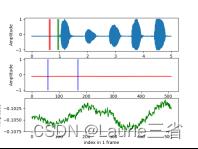
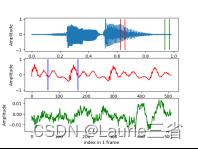
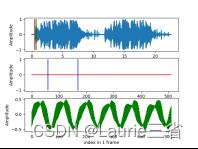
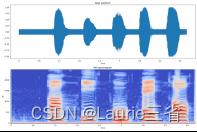
| 五. 实验结果与分析
| |||||||||||||||||||||||||||||||||||||
| 六.实验心得体会 通过本次实验,使我对于音频文件有了更深的理解,明白了音频的一些基本属性,如音高,音量等以及对于波形频谱的输出和PCM算法有了一定的认识. | |||||||||||||||||||||||||||||||||||||
FPGA与数字信号处理

过去十几年,通信与多媒体技术的快速发展极大地扩展了数字信号处理(DSP)的应用范围。眼下正在发生的是,以更高的速度和更低的成本实现越来越复杂的算法,这是针对高级信息服更高带宽以及增强的多媒体处理能力等需求的日益增加的结果。一些高性能应用正在不断发展,其中包括高级有线和无线音频、数据和视频处理。
通信和多媒体应用的发展,如互联网通信、安全无线通信以及消费娱乐设备,都在驱动着对能够有效实现复数运算和信号处理算法的高性能设备的需求。
这些应用中需要一些典型的DSP算法包括快速傅里叶变换(FFT)、离散余弦变换(DCT)、小波变换、数字滤波器(有限脉冲响应(FIR)、无限脉冲响应(IIR)和自适应滤波器)以及数字上下变频器。这些算法中,每一种都有一些结构性的元件可以用并行方法实现。而FPGA体系结构能够有效地实现并行运算。
数字滤波器:
数字滤波器通常用于修正和改变时域或频域中信号的特性。最为普通的数字滤波器就是线性时间不变(Linear Time-Invariant,LTI)滤波器。通常分为有限脉冲响应(FIR)和无限脉冲响应(IIR)两大类。
FIR滤波器:
有限长单位冲激响应滤波器,它可以在保证任意幅频特性的同时具有严格的线性相频特性,同时其单位抽样响应是有限长的,因而滤波器是稳定的系统。因此,FIR滤波器在通信、图像处理、模式识别等领域都有着广泛的应用。
FIR滤波处理如下式所示,其中x(n)为输入信号,h(n)为FIR滤波系数,y(n)为经过滤波后的信号;N表示FIR滤波器的抽头数,滤波器阶数为N-1。
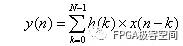
由上式可得到FIR滤波器在FPGA中的实现结构,如图1所示,主要由延迟单元Z-1、乘法器和累加器组成。此结构为直接型FIR滤波器结构,也称横向结构(transverse)。
FIR结构如下:
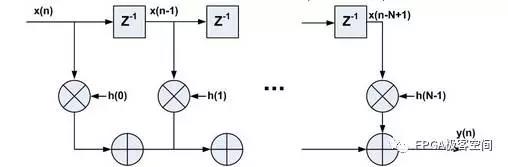
FIR滤波器结构
FIR滤波器广泛应用于数字信号处理中,主要功能就是将不感兴趣的信号滤除,留下有用信号。FIR滤波器是全零点结构,系统永远稳定;并且具有线性相位的特征,在有效频率范围内所有信号相位上不失真。详细算法这里不多做介绍。
IIR滤波器:
IIR--无限脉冲响应滤波器,它的设计理念是根据所要设计滤波器的参数去确定一个模拟滤波器的传输函数,然后再根据这个传输函数,通过双线性变换、或脉冲响应不变法来进行数字滤波器的设计。
其实际为递归滤波器,顾名思义,具有反馈。
IIR数字滤波器采用递归型结构,即结构上带有反馈环路。IIR滤波器运算结构通常由延时、乘以系数和相加等基本运算组成,可以组合成直接型、正准型、级联型、并联型四种结构形式,都具有反馈回路。
其他数字信号处理方法:
离散傅里叶变换
自适应滤波器
最小二乘法
NTT高效卷积
NTT快速卷积
CIC滤波器
与数字信号处理相关的技术:
矩形变换与数论变换
差错控制和加密技术
调制以及解调
FPGA在数字信号处理(DSP)中的使用
在FPGA内实现DSP功能具有以下优点:
-
-
性能提升
-
设计实现灵活性提高
-
系统级集成更高
-
通过一些设计调整的结合运用,基于FPGA的信号处理性能还可以获得进一步的提升。运算速度或者数据路径宽度都可以进一步提高,另外,时序操作可以在结构上增加一些并行度。这些措施中,每一种都可以提高一定的性能。在利用了目标FPGA器件灵活性的结构中实现算法,会获得比较大的好处。
利用FPGA,可以将多个设计功能集成到一个器件中。这种功能性的集成也可以提高性能、减小面积和功耗。
信号处理实现的另一个潜在的优点是,FPGA中包含一些预先验证过的信号处理算法单元。这些IP核或者块可以非常有效的实现一些常用的信号处理功能,使他们的性能达到最高。将多个高性能信号处理算法集成在一起,可以有效的降低成本、风险、,缩短开发时间。
设计考虑:
FPGA设计中一些注意事项对于下面列举的信号处理算法的实现非常重要。这些设计因素必须仔细的去实现,这样才能达到最高的性能,将设计实现的时间缩到最短。
-
-
同步设计的实现
-
模块化项目结构
-
时钟边界转换
-
时钟体系结构的实现
-
关键时钟与控制信号的布线
-
流水线深度和结构
-
有效的设计约束
-
信号处理算法架构的决策
-
加入良好的调试功能
-
随着FPGA技术的进步,在FPGA中实现信号处理算法正在成为有吸引力的替代方案,其实现成本也很诱人。在FPGA中实现信号处理算法,传统上的限制正在硬件和软件设计层次上逐渐被克服。FPGA硬件结构正在实现增强的DSP块。并具有更多的功能和更强的性能。系统级设计软件正在简化从块级到硬件描述语言(HDL),级的转换。一些系统工具中集成了流行的DSP算法开发工具(例如MATLAB),大大简化了FPGA中实现信号处理算法的过程。
版权所有权归卿萃科技,转载请注明出处。
作者:卿萃科技ALIFPGA
原文地址:卿萃科技FPGA极客空间 微信公众号

扫描二维码关注卿萃科技FPGA极客空间
以上是关于python《多媒体技术与应用》实验报告「数字音频处理」的主要内容,如果未能解决你的问题,请参考以下文章