SLAM学习笔记
Posted Kris_u
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了SLAM学习笔记相关的知识,希望对你有一定的参考价值。
相机按照工作方式不同,分为:
- 单目相机(Momocular):结构简单、成本低
- 双目相机(Stereo):双目相机的距离估计是比较左右眼的图像获得的。双目与多目的缺点是配置与标定较为复杂,其深度量程和精度受双目的基线与分辨率所限,而且视差的计算非常消耗资源,需要使用GPU和FPGA设备加速,才能实时输出整张图像的距离信息。现有条件下,计算量是双目的主要问题之一。
- 深度相机(RGB-D):其最大特点是可以通过红外结构或Time-of-Flight(ToF)原理,像激光传感器那样,通过主动向物体发射光并接收返回的光,测出物体与相机之间的距离。相比于双目可节省大量的计算资源。缺点:测量范围窄、噪声大、视野小、易受日光干扰、无法测量透射材质等诸多问题。slam方面主要用于室内,室外较难应用。
经典视觉SLAM框架
- 传感器信息读取。在视觉slam中主要为相机图像信息的读取和预处理。
- 前端视觉里程计(Visual Odemetry,VO):估计相邻图像间相机的运动,以及局部地图的样子。VO又称前端。
- 后端(非线性)优化(Optimazition)。后端接受不同时刻视觉里程计测量的相机位姿,以及回环检测的信息,对他们进行优化,得到全局一致的轨迹和地图。
- 回环检测(Loop Closure Detection)。回环检测判断机器人是否到达过先前的位置,如果监测到回环,他会把信息提供给后端进行处理。回环检测实质上是一种计算图像数据相似性的算法。
- 建图(Mapping)。它根据估计的轨迹,建立与任务要求对应的地图。构建地图的过程。
如果把工作环境限定在静态、刚体、光照变化不明显、没有人为干扰的场景,这种场景下的slam技术已经相当成熟。
度量地图(Metric Map):强调精确地表示地图中物体的位置关系,通常用稀疏(Sparse)与稠密(Dense)对其分类。定位时使用稀疏地图,导航使用稠密地图。
拓扑地图(Topological Map):是一个图,由节点个边组成只考虑节点的连通性。
视觉里程计
视觉里程计关心相邻图像之间的相机运动,最简单的情况是两张图像之间的运动关系。
视觉里程计能够通过相邻帧间的图像古遗迹相机运动,并恢复场景的空间结构。称它为‘里程计’是因为它和实际的里程计一样,只计算相邻时刻的运动,和过去的信息没有关联。
漂移:是由于视觉里程计的估计误差导致的,先前时刻的误差会传递到下一刻,导致经过一段时间后,估计的轨迹就不再准确。
后端优化和回环检测可以解决漂移问题。回环检测负责把“把机器人回到原始位置”的事情检测出来,后端优化则根据该信息校正整个轨迹的形状。
在视觉slam中,前端和计算机视觉研究领域更为相关,比如图像的特征提取与匹配等,后端则主要是滤波与非线性优化算法。
SLAM问题的本质:对运动物体自身和周围环境空间不确定性的估计。为解决slam问题,我们需要状态估计理论,把定位和见图的不确定性表达出来,然后采用滤波器或非线性优化,估计状态的均值和不确定性(方差)。
视觉回环检测实质上是一种计算图像数据相似性的算法。
SLAM问题的数学表述
离散 时刻: ;
;
轨迹: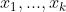 ;
;
路标:N个,用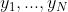 表示
表示
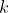 时刻位于
时刻位于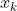 处探测到某一个路标
处探测到某一个路标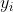
运动方程: 
这里,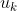 是运动传感器的读数或者输入,
是运动传感器的读数或者输入,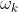 为该过程中加入的噪声。
为该过程中加入的噪声。
观测方程:在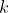 时刻位于
时刻位于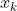 处探测到某一个路标
处探测到某一个路标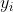 ,产生一个观测数据
,产生一个观测数据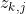 。用一个抽象函数h来描述这个关系:
。用一个抽象函数h来描述这个关系:

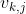 是这次观测里的噪声。
是这次观测里的噪声。
SLAM过程可以总结为两个基本方程:
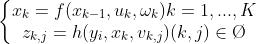
其中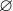 是一个集合,记录着哪个时刻观察到了哪个路标。这;两个方程描述了最基本的slam问题:
是一个集合,记录着哪个时刻观察到了哪个路标。这;两个方程描述了最基本的slam问题:
当知道运动测量的读数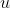 ,以及传感器的读数
,以及传感器的读数 ,如何求解定位问题(估计
,如何求解定位问题(估计 )和建图问题(估计
)和建图问题(估计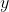 )?
)?
我们就把slam问题建模成了一个状态估计问题:如何通过带有噪声的测量数据,估计内部的、隐藏着的状态变量?
第3讲:三维空间刚体运动
三位空间的刚体运动描述方式:旋转矩阵、变换矩阵、四元数和欧拉角。
3.1旋转矩阵
1、内积
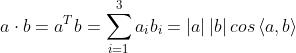
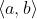 指向量
指向量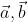 的夹角。 也可以描述向量间的投影关系。
的夹角。 也可以描述向量间的投影关系。
2、外积
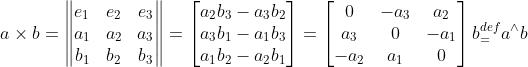
外积的结果是一个向量,他的方向垂直于这两个向量,大小为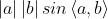 ,是两个向量张成的四边形的有向面积。
,是两个向量张成的四边形的有向面积。
反对称符号:^
反对称矩阵:
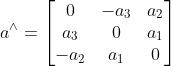
任意向量都对应着唯一的一个反对称矩阵,反之亦然。向量的加减法和内外积与坐标系无关。
3、刚体运动 :两个坐标之间的运动由一个旋转加上一个平移组成,这种运动成为刚体运动。
欧式变换由旋转和平移组成。

矩阵R描述了旋转本身。成为旋转矩阵(Rotation Matrix)。同时,该矩阵各分量是两个坐标系基的内积,由于基向量的程度为1,所以是各基向量夹角的余弦值。所以这个矩阵也叫方向余弦矩阵(Direction Cosine Matrix).
旋转矩阵是一个行列式为1的正交矩阵。反之,行列式为1 的正交矩阵也是一个旋转矩阵。可以将n维旋转矩阵的集合定义如下:
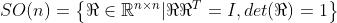
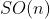 是特殊正交群。这个集合是由n维空间的旋转矩阵组成,特别地,
是特殊正交群。这个集合是由n维空间的旋转矩阵组成,特别地,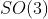 指三维空间的旋转。
指三维空间的旋转。
由于旋转矩阵为正交矩阵,它的逆(转置)描述了一个相反的旋转。按照上面的定义方式,有
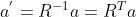
显然,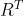 刻画了一个相反的旋转。
刻画了一个相反的旋转。
加上一次平移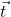 之后,
之后,
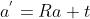
实际中,我们会定义坐标系1、坐标系2,那么向量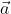 在两个坐标系下的坐标为
在两个坐标系下的坐标为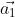 ,
,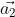 ,它们之间的关系是:
,它们之间的关系是:
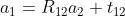
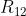 是指“把坐标系2的向量变换到坐标系1”中。
是指“把坐标系2的向量变换到坐标系1”中。
关于平移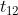 它实际对应的是坐标系1原点指向坐标系2原点的向量,在坐标系1下去的坐标。
它实际对应的是坐标系1原点指向坐标系2原点的向量,在坐标系1下去的坐标。
4、变换矩阵与齐次坐标
假设进行了两次变换: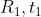 和
和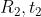 :
:
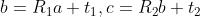
那么,从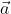 到
到 的变换为
的变换为
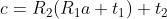
引入齐次坐标和变换矩阵:
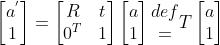
数学技巧:在三维向量的末位添加1,将其变为四维向量,称为齐次坐标。对于四维向量可以把旋转和平移写在一个矩阵里,使得整个关系变成线性关系,矩阵 称为变换矩阵(Transform Matrix)。
称为变换矩阵(Transform Matrix)。
关于变换矩阵 具有特殊的结构:左上角为旋转矩阵,右侧为平移变量,左下角为
具有特殊的结构:左上角为旋转矩阵,右侧为平移变量,左下角为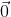 ,右下角为1.这种矩阵又称为特殊欧氏群(Special Euclidean Group):
,右下角为1.这种矩阵又称为特殊欧氏群(Special Euclidean Group):
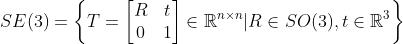
与SO(3)一样,求解该矩阵的逆表示一个反向的变换:

当写
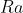 时,使用的是非齐次坐标。
时,使用的是非齐次坐标。
Eigen是一个C++开源线性代数库。它提供了快速的有关矩阵的线性代数运算,还包括解方程等。
它是一个纯用头文件搭建起来的库,只需要引入Eigen的头文件即可,不需要链接库文件。
Ubuntu 安装:
sudo apt install libeigen3-dev查找命令:
sudo updatedb
locate eigen33.3旋转向量和欧拉角
矩阵表示的缺点:
- SO(3)的旋转有9个量,但一次旋转只有3个自由度。因此表达式是冗余的。
- 旋转矩阵自身带有约束:他必须是个正交矩阵,且行列式为1.变换矩阵也是如此,这让求解变得更加困难。
任意一个旋转都可以用一个旋转轴和一个旋转角来刻画。
旋转向量:方向与旋转轴一致,长度等于旋转角。
考虑某个旋转用R表示。如果用旋转向量来描述,假设旋转轴为一个单位长度的向量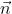 ,角度为
,角度为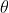 ,那么向量
,那么向量 也可以描述这个旋转。
也可以描述这个旋转。
从旋转向量到旋转矩阵的转换过程由罗德里格斯公式表明,
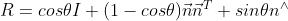
符号^是向量到反对称矩阵的转换符。反之。我们可以从一个旋转矩阵到旋转向量的转换。对于转角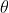 ,取两边的迹,有
,取两边的迹,有
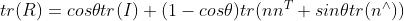

因此

关于旋转轴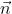 ,旋转轴上的向量在旋转后不发生改变,说明:
,旋转轴上的向量在旋转后不发生改变,说明:
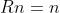
因此,旋转轴是矩阵R特征值1对应的特征向量。求解此方程,再归一化,就得到了旋转轴。
欧拉角:
使用3个分离的转角,把一个旋转分解成3次绕不同轴的旋转。
“偏航-俯仰-滚转”(yaw-pitch-roll)的旋转顺序等价于ZYX轴的旋转。
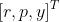 这样一个三维向量可以描述任意旋转。
这样一个三维向量可以描述任意旋转。
欧拉角的重大缺点是会碰到万向锁问题(Gimbal Lock):在俯仰角为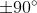 时,第一次旋转与第三次旋转将使用同一个轴。
时,第一次旋转与第三次旋转将使用同一个轴。
3.4四元数
四元数是Hamilton找到的一种扩展的复数。它既是紧凑的,也没有奇异性。
一个四元数有1个实部3个虚部。
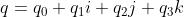
其中,i,j,k 为四元数的三个虚部。这三个虚部满足以下关系式:

人们也用一个标量和一个向量来表达四元数:
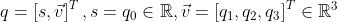
s称为四元数的实部,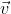 称为四元数的虚部。若虚部为
称为四元数的虚部。若虚部为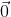 ,则称为实四元数 。若实部为0,则称虚四元数。
,则称为实四元数 。若实部为0,则称虚四元数。
可以用单位四元数表示三维空间中任意一个旋转。
1、四元数加减法:
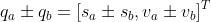
2、乘法(向量外积运算形式):
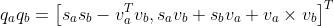
四元数乘法不可交换的,除非 和
和 在
在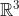 中共线,外积项为0.
中共线,外积项为0.
两个四元数的乘积仍是实的,这与复数一致。
3、模长
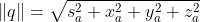
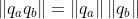
四元数乘积的模即模的乘积。
4、四元数的共轭是把虚部取成相反数:
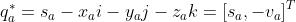
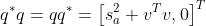
5、逆
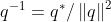
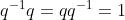
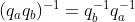
6、数乘、

四元数到其他旋转表示的转换
设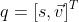 ,那么定义如下的符号+和
,那么定义如下的符号+和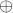 为:
为:
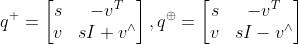
可证: 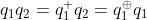
四元数到旋转矩阵的变换:
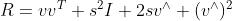
四元数到旋转向量的转换公式:
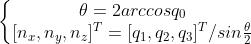
李群与李代数
什么样的相机位姿最符合当前观测数据?求得最优的R,t使得误差最小化。
旋转矩阵自身是带有约束的(正交且行列式为1)。它们作为优化变量时,会引入额外的约束,使优化变得困难。通过李群与李代数的关系,我们希望把位姿估计变成无约束的优化问题,简化求解方式。
三维旋转矩阵构成了特殊正交群SO(3); 变换矩阵构成了特殊欧式群SE(3).

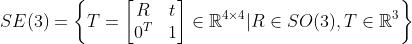
旋转矩阵和变换矩阵对加法不封闭:任意两个旋转矩阵的和不再是旋转矩阵。SO(3)和SE(3)关于乘法封闭。
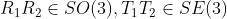
乘法对应着旋转或变换的复合,两个旋转矩阵相乘表示做了两次旋转。对于这种只有一个(良好)运算的集合,称为群。
群(Group):一种集合加上一种运算的代数结构。集合记作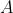 ,运算记作
,运算记作 ,那么
,那么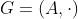
- 封闭性:
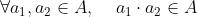
- 结合律:
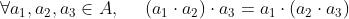
- 幺元:
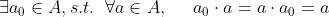
- 逆:
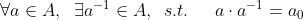
李群是指具有连续(光滑)性质的群。
每个李群都有与之对应的李代数。李代数描述了李群的局部性质,准确的说,是单位元附近的正切空间。一般的李代数定义如下:
李代数由一个集合V、一个数域和一个二元运算[,]组成。如果满足一下几条性质,则称(V,F,[,])为一个李代数,记作g。
- 封闭性

- 双线性
 有
有
- 自反性
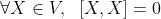
- 雅可比等价

其中,二元运算被称为李括号。
李代数
SO(3)对应的李代数是定义在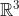 上的向量,我们记作
上的向量,我们记作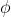 。每个
。每个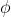
都可以生成一个反对称矩阵:
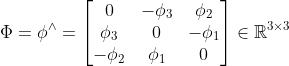

 是一个由三维向量组成的集合,每个向量对应一个反对称矩阵,可以用于表达旋转矩阵的倒数。它与SO(3)的关系由指数映射给定:
是一个由三维向量组成的集合,每个向量对应一个反对称矩阵,可以用于表达旋转矩阵的倒数。它与SO(3)的关系由指数映射给定:
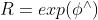
李代数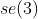
对于SE(3),有对应的李代数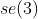 ,
,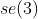 位于
位于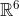 空间中:
空间中:

我们把每个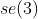 元素记作
元素记作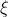 ,它是一个6维向量。前三维为平移(但含义与变换矩阵中的平移不同)记作
,它是一个6维向量。前三维为平移(但含义与变换矩阵中的平移不同)记作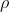 ;后三维为旋转,记作
;后三维为旋转,记作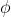 ,实质上是
,实质上是  元素。
元素。
使用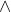 和
和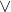 符号指代“从向量到矩阵”和“从矩阵到向量”的关系。
符号指代“从向量到矩阵”和“从矩阵到向量”的关系。
指数与对数映射
任意矩阵的指数映射可以写成一个泰勒展开,但是只有在收敛的情况下才会有结果,其结果仍是一个矩阵:
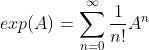
对于 中的任意元素
中的任意元素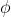 ,也可按此方式定义它的指数映射:
,也可按此方式定义它的指数映射:
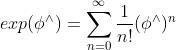
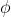 三维向量,定义其模长和方向,分别记作
三维向量,定义其模长和方向,分别记作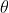 和
和 , 于是
, 于是 ,这里a是一个长度为1 的方向向量,即
,这里a是一个长度为1 的方向向量,即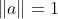 .首先,对于
.首先,对于 ,有一下两条性质:
,有一下两条性质:


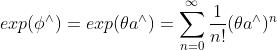
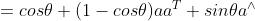
最后得到一个似曾相识的式子:
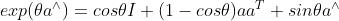
它和罗德里格斯公式如出一辙。  实际上就是所谓的旋转向量组成的空间,而指数映射即罗德里格斯公式。通过他们,我们把
实际上就是所谓的旋转向量组成的空间,而指数映射即罗德里格斯公式。通过他们,我们把 中任意一个向量对应到了一个位于SO(3)中的旋转矩阵。反之,如果定义对数映射,也能把SO(3)中的元素对应到
中任意一个向量对应到了一个位于SO(3)中的旋转矩阵。反之,如果定义对数映射,也能把SO(3)中的元素对应到 中:
中:

和指数映射一样,我们没有必要直接用泰勒展开计算对数映射。利用迹的性质分别求解转角和转轴,采用这种方式更省事。
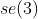 上的指数映射形式如下:
上的指数映射形式如下:
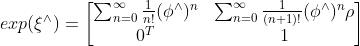
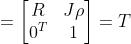
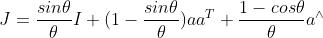
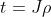

以上是关于SLAM学习笔记的主要内容,如果未能解决你的问题,请参考以下文章