如何用python实现网络图节点权重的添加以及如何把一个非连通的大网络图分成多个小网络图
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何用python实现网络图节点权重的添加以及如何把一个非连通的大网络图分成多个小网络图相关的知识,希望对你有一定的参考价值。
networkx是python的一个库,它为图的数据结构提供算法、生成器以及画图工具。近日在使用ryu进行最短路径获取,可以通过该库来简化工作量。该库采用函数方式进行调用相应的api,其参数类型通常为图对象。函数API的调用,按照以下步骤来创建构建图:
1.networkx的加载
在python中调用networkx通常只需要将该库导入即可
import networkx as nx
2.图对象的创建
networkx提供了四种基本图对象:Graph,DiGraph,MultiGraph,MultiDiGraph。
使用如下调用方式,可以创建以上四种图对象的空图。
G=nx.Graph()
G=nx.DiGraph()
G=nx.MultiGraph()
G=nx.MultiDiGraph()
在 networkx中,图的各个节点允许以哈希表对象来表示,而对于图中边的各个参量,则可以通过与边相关联的方式来标识,一般而言,对于权重,用weight作为keyword,而对于其他的参数,使用者可以采用任何除weight以外的keyword来命名。
3.在2中,创建的只是一副空图,为了得到一个有节点、有边的图,一般采用下面这个函数:
1
2
G.add_edge(1,2) #default edge data=1
G.add_edge(1,2) #specify edge data=0.9
add_edge()函数,该函数在调用时需要传入两个参数u和v,以及多个可选参数
u和v即图中的两个节点,如果图中不存在节点,在调用时会自动将这两个节点添加入内,同时构建两个节点之间的连接关系,可选参数通常指这条边的权重等关系参量。需要注意的是,如果图中已经存在了这条边,重新进行添加时会对这条边进行跟新操作(也就是覆盖了原有的信息)。
对于该函数,除了上述的构建方式以外,还有以下几种方式来创建边:
1
2
3
G.add_edge(*e) # single edge as tuple of two nodes
G.add_edge(1, 3, weight=7, capacity=15, length=342.7) #using many arguements to create edge
G.add_edges_from( [(1, 2)] ) # add edges from iterable container
有时候,当采用默认方式创建边以后,我们可能还会往边里面添加边的相关参数,这时候,可以采用下面的方式来更新边的信息:
1
2
3
4
5
#For non-string attribute keys, use subscript notation.
G.add_edge(1, 2)
G[1][2].update(0: 5) #更新边的信息
G.edges[1, 2].update(0: 5) #更新边的信息
#上述两种更新方式,择一选取即可
细心的朋友可能注意到我在写创建图的内容的时候,提到了add_edges_from()函数,该函数也是用来创建边的,该方式与add_edges()略有不同,比之add_edges()采用一个一个节点的方式进行创建,它来的更为便利。这个函数在调用时,需要一个节点元组作为参数以及多个可选参数作为边的信息。你可以这么传递:
默认创建节点之间的边:
1
G.add_edges_from([(u,v)])
也可以这么写,在创建的同时添加信息:
1
G.add_edges_from([(3, 4), (1, 4)], label=\'WN2898\')
通过上述方式,就构建了一个3-4-1的图的连接,并给每条边打上了标签。
由此你就可以创建出自己的图模型了。追问
您说的这些,实现了对边权的添加,请问,如果要创建的图中即有边权又有点权呢,这个节点的权重怎么添加?
参考技术A 请问一下题主这个问题解决了吗 想知道答案如何用Python实现常见机器学习算法-3
三、BP神经网络
1、神经网络模型
首先介绍三层神经网络,如下图
输入层(input layer)有三个units(![]() 为补上的bias,通常设为1)
为补上的bias,通常设为1)
![]() 表示第j层的第i个激励,也称为单元unit
表示第j层的第i个激励,也称为单元unit
![]() 为第j层到第j+1层映射的权重矩阵,就是每条边的权重
为第j层到第j+1层映射的权重矩阵,就是每条边的权重

所以可以得到:
隐含层:

输出层:
![]()
其中,S型函数![]() ,也成为激励函数
,也成为激励函数
可以看出![]() 为3✖️4的矩阵,
为3✖️4的矩阵,![]() 为1✖️4的矩阵
为1✖️4的矩阵
![]() ==》j+1的单元数x(j层的单元数+1)
==》j+1的单元数x(j层的单元数+1)
2、代价函数
假设最后输出的![]() ,即代表输出层有K个单元
,即代表输出层有K个单元

其中,![]() 代表第i个单元输出与逻辑回归的代价函数
代表第i个单元输出与逻辑回归的代价函数

差不多,就是累加上每个输出(共有K个输出)
3、正则化
L-->所有层的个数
![]() -->第l层unit的个数
-->第l层unit的个数
正则化后的代价函数为
![]()
![]() 共有L-1层,然后是累加对应每一层的theta矩阵,注意不包含加上偏置项对应的theta(0)
共有L-1层,然后是累加对应每一层的theta矩阵,注意不包含加上偏置项对应的theta(0)
正则化后的代价函数实现代码:
1 # 代价函数 2 def nnCostFunction(nn_params,input_layer_size,hidden_layer_size,num_labels,X,y,Lambda): 3 length = nn_params.shape[0] # theta的中长度 4 # 还原theta1和theta2 5 Theta1 = nn_params[0:hidden_layer_size*(input_layer_size+1)].reshape(hidden_layer_size,input_layer_size+1) 6 Theta2 = nn_params[hidden_layer_size*(input_layer_size+1):length].reshape(num_labels,hidden_layer_size+1) 7 8 # np.savetxt("Theta1.csv",Theta1,delimiter=\',\') 9 10 m = X.shape[0] 11 class_y = np.zeros((m,num_labels)) # 数据的y对应0-9,需要映射为0/1的关系 12 # 映射y 13 for i in range(num_labels): 14 class_y[:,i] = np.int32(y==i).reshape(1,-1) # 注意reshape(1,-1)才可以赋值 15 16 \'\'\'去掉theta1和theta2的第一列,因为正则化时从1开始\'\'\' 17 Theta1_colCount = Theta1.shape[1] 18 Theta1_x = Theta1[:,1:Theta1_colCount] 19 Theta2_colCount = Theta2.shape[1] 20 Theta2_x = Theta2[:,1:Theta2_colCount] 21 # 正则化向theta^2 22 term = np.dot(np.transpose(np.vstack((Theta1_x.reshape(-1,1),Theta2_x.reshape(-1,1)))),np.vstack((Theta1_x.reshape(-1,1),Theta2_x.reshape(-1,1)))) 23 24 \'\'\'正向传播,每次需要补上一列1的偏置bias\'\'\' 25 a1 = np.hstack((np.ones((m,1)),X)) 26 z2 = np.dot(a1,np.transpose(Theta1)) 27 a2 = sigmoid(z2) 28 a2 = np.hstack((np.ones((m,1)),a2)) 29 z3 = np.dot(a2,np.transpose(Theta2)) 30 h = sigmoid(z3) 31 \'\'\'代价\'\'\' 32 J = -(np.dot(np.transpose(class_y.reshape(-1,1)),np.log(h.reshape(-1,1)))+np.dot(np.transpose(1-class_y.reshape(-1,1)),np.log(1-h.reshape(-1,1)))-Lambda*term/2)/m 33 34 return np.ravel(J)
4、反向传播BP
上面正向传播可以计算得到J(θ),使用梯度下降算法还需要求它的梯度
BP反向传播的目的就是求代价函数的梯度
假设4层的神经网络,![]() 记为-->l层第j个单元的误差
记为-->l层第j个单元的误差
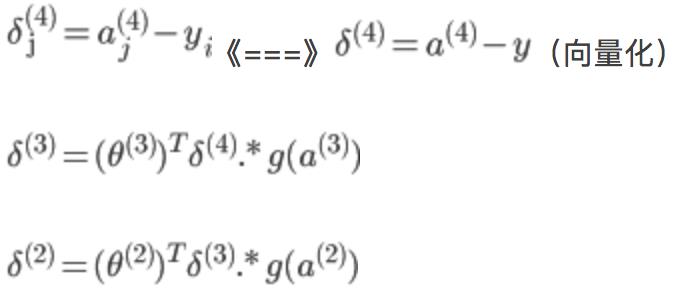
没有![]() ,因为对于输入没有误差,因为S型函数
,因为对于输入没有误差,因为S型函数![]() 的倒数为:
的倒数为:
![]()
所以上面的![]() 和
和![]() 可以在前向传播中计算出来
可以在前向传播中计算出来
反向传播计算梯度的过程为:
![]()
for i=1-m:
![]()
正向传播计算![]() (l=2,3,4...L)
(l=2,3,4...L)

最后![]() ,即得到代价函数的梯度
,即得到代价函数的梯度
代码实现:
1 # 梯度 2 def nnGradient(nn_params,input_layer_size,hidden_layer_size,num_labels,X,y,Lambda): 3 length = nn_params.shape[0] 4 Theta1 = nn_params[0:hidden_layer_size*(input_layer_size+1)].reshape(hidden_layer_size,input_layer_size+1) 5 Theta2 = nn_params[hidden_layer_size*(input_layer_size+1):length].reshape(num_labels,hidden_layer_size+1) 6 m = X.shape[0] 7 class_y = np.zeros((m,num_labels)) # 数据的y对应0-9,需要映射为0/1的关系 8 # 映射y 9 for i in range(num_labels): 10 class_y[:,i] = np.int32(y==i).reshape(1,-1) # 注意reshape(1,-1)才可以赋值 11 12 \'\'\'去掉theta1和theta2的第一列,因为正则化时从1开始\'\'\' 13 Theta1_colCount = Theta1.shape[1] 14 Theta1_x = Theta1[:,1:Theta1_colCount] 15 Theta2_colCount = Theta2.shape[1] 16 Theta2_x = Theta2[:,1:Theta2_colCount] 17 18 Theta1_grad = np.zeros((Theta1.shape)) #第一层到第二层的权重 19 Theta2_grad = np.zeros((Theta2.shape)) #第二层到第三层的权重 20 21 Theta1[:,0] = 0; 22 Theta2[:,0] = 0; 23 \'\'\'正向传播,每次需要补上一列1的偏置bias\'\'\' 24 a1 = np.hstack((np.ones((m,1)),X)) 25 z2 = np.dot(a1,np.transpose(Theta1)) 26 a2 = sigmoid(z2) 27 a2 = np.hstack((np.ones((m,1)),a2)) 28 z3 = np.dot(a2,np.transpose(Theta2)) 29 h = sigmoid(z3) 30 31 \'\'\'反向传播,delta为误差,\'\'\' 32 delta3 = np.zeros((m,num_labels)) 33 delta2 = np.zeros((m,hidden_layer_size)) 34 for i in range(m): 35 delta3[i,:] = h[i,:]-class_y[i,:] 36 Theta2_grad = Theta2_grad+np.dot(np.transpose(delta3[i,:].reshape(1,-1)),a2[i,:].reshape(1,-1)) 37 delta2[i,:] = np.dot(delta3[i,:].reshape(1,-1),Theta2_x)*sigmoidGradient(z2[i,:]) 38 Theta1_grad = Theta1_grad+np.dot(np.transpose(delta2[i,:].reshape(1,-1)),a1[i,:].reshape(1,-1)) 39 40 \'\'\'梯度\'\'\' 41 grad = (np.vstack((Theta1_grad.reshape(-1,1),Theta2_grad.reshape(-1,1)))+Lambda*np.vstack((Theta1.reshape(-1,1),Theta2.reshape(-1,1))))/m 42 return np.ravel(grad)
5、BP可以求梯度的原因
实际是利用了链式求导法则
因为下一层的单元利用上一层的单元作为输入进行计算
大体的推导过程如下,最终我们是想预测函数与已知的y非常接近,求均方差的梯度沿着此梯度方向可使代价函数最小化。可对照上面求梯度的过程。

求误差更详细的推导过程:

6、梯度检查
检查利用BP求的梯度是否正确
利用导数的定义验证:

求出来的数值梯度应该与BP求出的梯度非常接近
验证BP正确后就不需要再执行验证梯度的算法了
代码实现
1 # 检验梯度是否计算正确 2 # 检验梯度是否计算正确 3 def checkGradient(Lambda = 0): 4 \'\'\'构造一个小型的神经网络验证,因为数值法计算梯度很浪费时间,而且验证正确后之后就不再需要验证了\'\'\' 5 input_layer_size = 3 6 hidden_layer_size = 5 7 num_labels = 3 8 m = 5 9 initial_Theta1 = debugInitializeWeights(input_layer_size,hidden_layer_size); 10 initial_Theta2 = debugInitializeWeights(hidden_layer_size,num_labels) 11 X = debugInitializeWeights(input_layer_size-1,m) 12 y = 1+np.transpose(np.mod(np.arange(1,m+1), num_labels))# 初始化y 13 14 y = y.reshape(-1,1) 15 nn_params = np.vstack((initial_Theta1.reshape(-1,1),initial_Theta2.reshape(-1,1))) #展开theta 16 \'\'\'BP求出梯度\'\'\' 17 grad = nnGradient(nn_params, input_layer_size, hidden_layer_size, 18 num_labels, X, y, Lambda) 19 \'\'\'使用数值法计算梯度\'\'\' 20 num_grad = np.zeros((nn_params.shape[0])) 21 step = np.zeros((nn_params.shape[0])) 22 e = 1e-4 23 for i in range(nn_params.shape[0]): 24 step[i] = e 25 loss1 = nnCostFunction(nn_params-step.reshape(-1,1), input_layer_size, hidden_layer_size, 26 num_labels, X, y, 27 Lambda) 28 loss2 = nnCostFunction(nn_params+step.reshape(-1,1), input_layer_size, hidden_layer_size, 29 num_labels, X, y, 30 Lambda) 31 num_grad[i] = (loss2-loss1)/(2*e) 32 step[i]=0 33 # 显示两列比较 34 res = np.hstack((num_grad.reshape(-1,1),grad.reshape(-1,1))) 35 print res
7、权重的随机初始化
神经网络不能像逻辑回归那样初始化theta为0,因为若是每条边的权重都为0,每个神经元都是相同的输出,在反向传播中也会得到同样的梯度,最终只会预测一种结果。
所以应该初始化为接近0的数
代码实现
1 # 随机初始化权重theta 2 def randInitializeWeights(L_in,L_out): 3 W = np.zeros((L_out,1+L_in)) # 对应theta的权重 4 epsilon_init = (6.0/(L_out+L_in))**0.5 5 W = np.random.rand(L_out,1+L_in)*2*epsilon_init-epsilon_init # np.random.rand(L_out,1+L_in)产生L_out*(1+L_in)大小的随机矩阵 6 return W
8、预测
正向传播预测结果
代码实现
1 # 预测 2 def predict(Theta1,Theta2,X): 3 m = X.shape[0] 4 num_labels = Theta2.shape[0] 5 #p = np.zeros((m,1)) 6 \'\'\'正向传播,预测结果\'\'\' 7 X = np.hstack((np.ones((m,1)),X)) 8 h1 = sigmoid(np.dot(X,np.transpose(Theta1))) 9 h1 = np.hstack((np.ones((m,1)),h1)) 10 h2 = sigmoid(np.dot(h1,np.transpose(Theta2))) 11 12 \'\'\' 13 返回h中每一行最大值所在的列号 14 - np.max(h, axis=1)返回h中每一行的最大值(是某个数字的最大概率) 15 - 最后where找到的最大概率所在的列号(列号即是对应的数字) 16 \'\'\' 17 #np.savetxt("h2.csv",h2,delimiter=\',\') 18 p = np.array(np.where(h2[0,:] == np.max(h2, axis=1)[0])) 19 for i in np.arange(1, m): 20 t = np.array(np.where(h2[i,:] == np.max(h2, axis=1)[i])) 21 p = np.vstack((p,t)) 22 return p
9、输出结果
梯度检查

随机显示100个手写数字

显示theta1权重

训练集预测准确度

归一化后训练集预测准确度

以上是关于如何用python实现网络图节点权重的添加以及如何把一个非连通的大网络图分成多个小网络图的主要内容,如果未能解决你的问题,请参考以下文章