机器学习系列（三十六）——回归决策树与决策树总结

Posted 2023-03-25

参考技术A

回归决策树树是用于回归的决策树模型，回归决策树主要指CART算法， 同样也为二叉树结构。以两个特征预测输出的回归问题为例，回归树的原理是将特征平面划分成若干单元，每一个划分单元都对应一个特定的输出。因为每个结点都是yes和no的判断，所以划分的边界是平行于坐标轴的。对于测试数据，我们只要将特征按照决策过程将其归到某个单元，便得到对应的回归输出值。

如上图所示的划分和相应的回归树，如果现在新来一个数据的特征是(6,7.5)，按照回归树，它对应的回归结果就是C5。节点的划分的过程也就是树的建立过程，每划分一次，随即确定划分单元对应的输出，也就多了一个结点。当根据相应的约束条件终止划分的时候，最终每个单元的输出也就确定了，输出也就是叶结点。这看似和分类树差不多，实则有很大的区别。划分点的寻找和输出值的确定是回归决策树的两个核心问题。
一个输入空间的划分的误差是用真实值和划分区域的预测值的最小二乘来衡量的：

其中， 是每个划分单元的预测值，这个预测值是该单元内每个样本点的值的某种组合，比如可取均值：

（输入特征空间划分为 ）
那么求解最优划分即是求解最优化问题：

其中， 和 是每次划分形成的两个区域。
关于该最优化问题的求解这里不再介绍，下面直接使用skleaen中的决策回归树来看一下决策树的回归效果，数据集使用Boston房价数据：

不进行调参的话，可以看到在测试集上R方是0.59，显然这是不太好的结果，但是一个有趣的现象是，在训练集上：

R方值是1.0，也就是在训练集上决策树预测的回归结果完全吻合毫无偏差，这显然是过拟合。这个例子也说明了决策树算法是非常容易产生过拟合的，当然我们可以通过调参来缓解过拟合。

下面绘制学习曲线来直观看一下决策树回归模型的表现，首先绘制基于MSE的学习曲线：

学习曲线如下：

再绘制基于R方的学习曲线：

上面两种都是在默认情况下也就是不进行决策树深度和叶子节点个数等条件的限制得到的结果。发现在训练集上，如果不进行限制，可以做到0偏差，这是明显的过拟合。接下来调节参数再绘制学习曲线，为节约篇幅，只调节决策树深度这一个参数，而且只绘制基于R方的学习曲线：
max_depth=1时

max_depth=3时

max_depth=5时

随着深度的增加，模型复杂度越来越高，过拟合现象也越来越明显，可以测试，当max_depth=20时，在训练集上又为一条y=1的无偏差直线。有兴趣的仍然可以修改其它参数绘制学习曲线。

决策树的局限性：

使用本系列上篇文章中的鸢尾花数据，来看一下决策树对个别数据敏感会导致的结果，在本系列上篇文章中，使用信息熵划分，其余参数默认情况下绘制的决策边界是：

接着我们删除索引为138的数据，再来绘制决策边界：

发现此时的决策边界已经完全不同了，而这仅仅只是一个数据点的影响。

综上我们知道决策树实际是一种不够稳定的算法，它的表现极度依赖调参和数据，不过虽然决策树本身不是一种高效的机器学习算法，但是它们基于集成学习的组合——随机森林(RF)却是一个很鲁棒的机器学习算法，这将在下篇开始介绍。

机器学习：通俗易懂决策树与随机森林及代码实践

与SVM一样，决策树是通用的机器学习算法。随机森林，顾名思义，将决策树分类器集成到一起就形成了更强大的机器学习算法。它们都是很基础但很强大的机器学习工具，虽然我们现在有更先进的算法工具来训练模型，但决策树与随机森林因其简单灵活依然广受喜爱，建议大家学习。

一、决策树

1.1 什么是决策树

我们可以把决策树想象成IF/ELSE判别式深度嵌套的二叉树形结构。以我们在所举的鸢尾花数据集为例。

我们曾用seaborn绘制花瓣长度和宽度特征对应鸢尾花种类的散点图，如下：

当花瓣长度小于2.45则为山鸢尾(setosa)，剩下的我们判断花瓣宽度小于1.75则为变色鸢尾(versicolor)剩下的为维吉尼亚鸢尾(virginica)。那么我用导图画一下这种判别式的树形结构如下：

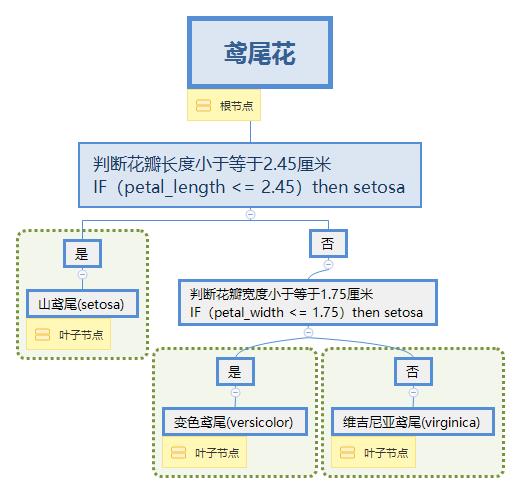
因此，当我们面对任意鸢尾花的样本，我们只需要从根节点到叶子节点遍历决策树，就可以得到鸢尾花的分类结论。

这就是决策树。

1.2 决策树代码实践

我们导入数据集（大家不用在意这个域名），并训练模型：

import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier

#引入数据集
df = pd.read_csv('https://blog.caiyongji.com/assets/iris.csv')

#决策树模型
X = df[['petal_length','petal_width']].to_numpy() 
y = df['species']
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)

我们来可视化决策树：

import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
plt.figure(figsize=(12,8))
plot_tree(tree_clf,filled=True);

如上图，我们可以看到根节点总实例数为150时，由value = [50, 50, 50]可知，实际样本分类为50个山鸢尾花实例、50个变色鸢尾花实例、50个维吉尼亚鸢尾花实例。我们再看最末尾右侧的叶子节点（紫色），由value = [0, 1, 45]可知，实际样本分类为0个山鸢尾花实例、1个变色鸢尾花实例、45个维吉尼亚鸢尾花实例。

那么gini = 0.043是什么意思呢？

1.3 基尼不纯度

显然我们进行分类时，每一个类别实际混入其他类的数量越少分类就越纯粹，这种纯度我们通过如下公式表示：

我们计算维吉尼亚鸢尾花节点（紫色）的gini系数1-((0/46)**2 + (1/46)**2 + (45/46)**2) = 0.04253308128544431 ≈0.043 。

我们使用基尼(gini)不纯度来衡量决策树的好坏。那么我们通过最小化基尼不纯度min(gini)来求解X[0],X[1]（即，花瓣长度宽度特征）边界的过程就决策树模型的训练过程。

二、随机森林

2.1 大数定理与随机森林

其实随机森林很简单，我们把决策树随机组合在一起就是随机森林，它比单个的决策树更有效。

凭什么？

假设我们有一枚不均匀的硬币，投掷它有51%的概率为正面，49%的概率为背面，那么当投掷1000次时，“大多数为正面"这件事的概率为75%。投掷10000次时，“大多数为正面"这件事的概率为97%。这就是大数定理，它体现的是群体智慧。质量不够，数量来凑。由此可知，当前寻找最佳模型的方法不止是技巧的比拼，也同样是算力的比拼。

2.2 随机森林代码实践

2.2.1. 引入新的数据集

添加引用：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

导入数据集（大家不用在意这个域名）：

df = pd.read_csv("https://blog.caiyongji.com/assets/penguins_size.csv")
df = df.dropna()
df.head()

species	island	culmen_length_mm	culmen_depth_mm	flipper_length_mm	body_mass_g	sex
Adelie	Torgersen	39.1	18.7	181	3750	MALE
Adelie	Torgersen	39.5	17.4	186	3800	FEMALE
Adelie	Torgersen	40.3	18	195	3250	FEMALE
Adelie	Torgersen	36.7	19.3	193	3450	FEMALE
Adelie	Torgersen	39.3	20.6	190	3650	MALE

企鹅数据集包含特征和标签如下：

• 特征：所在岛屿island、鸟喙长度culmen_length_mm、鸟喙深度culmen_depth_mm、脚蹼长度flipper_length_mm、体重(g)、性别
• 标签：物种species：Chinstrap, Adélie, or Gentoo

2.2.2 观察数据

sns.pairplot(df,hue='species')

我们通过pairplot方法绘制特征两两之间的对应关系。

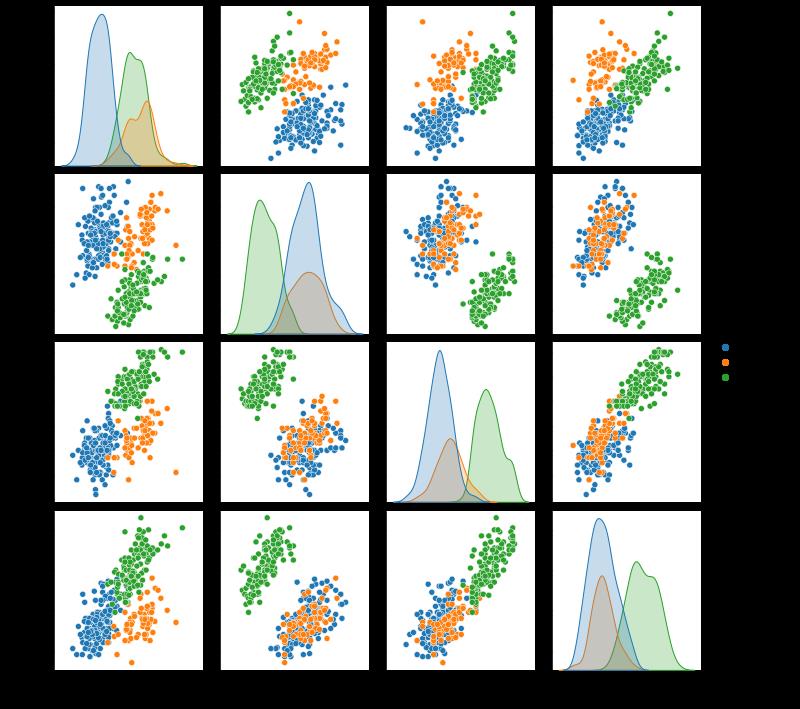
2.2.3 预处理

X = pd.get_dummies(df.drop('species',axis=1),drop_first=True)
y = df['species']
X.head()

注意，get_dummies方法将字符串属性的列转换成了数字属性的多个列。如，岛屿island和性别sex分别转换成了island_Dream、island_Torgersen和sex_FEMALE、sex_MALE。这是一种独热编码的关系，比如sex_FEMALE与sex_MALE属性独立，在空间内没有向量关系。

culmen_length_mm	culmen_depth_mm	flipper_length_mm	body_mass_g	island_Dream	island_Torgersen	sex_FEMALE	sex_MALE
39.1	18.7	181	3750	0	1	0	1
39.5	17.4	186	3800	0	1	1	0
40.3	18	195	3250	0	1	1	0
36.7	19.3	193	3450	0	1	1	0
39.3	20.6	190	3650	0	1	0	1

2.2.4 训练数据

#训练
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=101)
model = RandomForestClassifier(n_estimators=10,max_features='auto',random_state=101)
model.fit(X_train,y_train)

#预测
from sklearn.metrics import accuracy_score
preds = model.predict(X_test)
accuracy_score(y_test,preds)

使用随机森林分类器RandomForestClassifier训练，得到模型精度为97%。

2.2.5 网格搜索与AdaBoost提升法（拓展）

我们使用AdaBoostClassifier分类器集成数个决策树分类器DecisionTreeClassifier进行分类。并使用网格搜索方法GridSearchCV来寻找最优参数。

from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import AdaBoostClassifier

ada_clf = AdaBoostClassifier(DecisionTreeClassifier(max_depth=1), random_state=101)
ada_clf.fit(X_train, y_train)
param_grid = {'n_estimators':[10,15,20,25,30,35,40], 'learning_rate':[0.01,0.1,0.5,1], 'algorithm':['SAMME', 'SAMME.R']}
grid = GridSearchCV(ada_clf,param_grid)
grid.fit(X_train,y_train)
print("grid.best_params_ = ",grid.best_params_,", grid.best_score_ =" ,grid.best_score_)

这是一种集成学习技术，输出如下：

grid.best_params_ =  {'algorithm': 'SAMME', 'learning_rate': 1, 'n_estimators': 20} , grid.best_score_ = 0.9914893617021276

总结

二叉树是决策树的核心逻辑，随机森林是大数定理的应用实现。这种基本思想即使不用数学公式也可以很容易的解释清楚，这也是我做这个系列课程（文章）的主要风格特点。我认为，数学是对现实世界的解释，但现实世界并不能被数学完全解释。像谷歌AI主管Laurence Moroney所说：

很多人害怕数学，害怕大量的深度的微积分知识。其实我们可以实现编码而不考虑数学，我们可以使用TensorFlow中高(层)级的API，来解决问题，如自然语言处理，图像分类，计算机视觉序列模型等而无需理解深刻的数学。就像你使用JAVA却不一定非要掌握它是如何编译的。未来，AI只是每个开发者技术栈(toolbox)中的一部分，就像HTML, CSS, JAVA。

希望那一天可以早点到来吧……

往期文章：

以上是关于机器学习系列（三十六）——回归决策树与决策树总结的主要内容，如果未能解决你的问题，请参考以下文章

R语言机器学习 | 8 决策树与集成学习

Python机器学习实战决策树与集成学习——集成学习GBDT应用实例

分类:基本概念、决策树与模型评估

决策树系列决策树基础

机器学习：通俗易懂决策树与随机森林及代码实践

机器学习算法基础+实战系列决策树算法