图像边缘检测:Canny算子、Prewitt算子和sobel算子
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图像边缘检测:Canny算子、Prewitt算子和sobel算子相关的知识,希望对你有一定的参考价值。
参考技术A 边缘检测是检测图像中的一些像素点,它们周围的像素点的灰度发生了急剧的变化,我们认为在这过程中,图像中的物体不同导致了这一变化,因此可以将这些像素点作为一个集合,可以用来标注图像中不同物体的边界。边缘区域的灰度剖面可以看作是一个阶跃,即图像的灰度在一个很小的区域内变化到另一个相差十分明显的区域。边缘是图像中的重要的结构性特征,边缘往往存在于目标和背景之间,不同的区域之间,因此它可以作为图像分割的重要依据。在边缘检测中,它提取的是图像中不连续部分的特征,将闭合的边缘提取出来便可以作为一个区域。与区域划分相比,边缘检测不需要逐个的对像素进行比较,比较适合大图像的处理.如图
边缘其实就是图像上灰度级变化很快的点的集合。这些点往往梯度很大。图像的梯度可以用一阶导数和二阶偏导数来求解。但是图像以矩阵的形式存储的,不能像数学理论中对直线或者曲线求导一样,对一幅图像的求导相当于对一个平面、曲面求导。对图像的操作,我们采用模板对原图像进行卷积运算,从而达到我们想要的效果。而获取一幅图像的梯度就转化为:模板(Roberts、Prewitt、Sobel、Lapacian算子)对原图像进行卷积。
使用一阶导的算子有,prewitt,sobel和canny;使用二阶导的有lapacian
(1)一阶导算子:
1、prewitt
通常用 f '(x) = f(x + 1) - f(x - 1) 近似计算一阶差分。可以提出系数:[-1, 0, 1],这个就是模板。在二维情况下是:
-1, 0, 1
-1, 0, 1
-1, 0, 1
这个就是prewitt算子。即
f(x-1, y-1), f(x, y-1), f(x+1, y-1)
f(x-1, y), f(x, y), f(x+1, y)
f(x-1, y+1), f(x, y+1), f(x+1, y+1)
2、sobel
中心点 f(x, y) 是重点考虑的,它的权重应该多一些,所以改进成下面这样的
-1, 0, 1
-2, 0, 2
-1, 0, 1
这就是 Sobel 边缘检测算子,偏 x 方向的。同理可得偏y方向上的。
-1, -2, -1
0, 0, 0
1, 2, 1
分别计算偏 x 方向的 Gx,偏 y 方向的 Gy,求绝对值,压缩到 [0, 255]区间,即 G(x, y) = Gx + Gy 就是 sobel 边缘检测后的图像了。因此sobel算子是有两个方向的。
3、canny
canny算子的计算步骤如下:
1.高斯滤波器平滑图像。去除噪声
2.一阶差分偏导计算梯度值和方向。通过sobel算子计算的。
3.对梯度值不是极大值的地方进行抑制。把不是极值的点,全部置0,去掉了大部分弱的边缘。所以图像边缘会变细。
4.用双阈值连接图上的联通点。设置双阈值 t1, t2, 是这样的,t1 <= t2 大于 t2 的点肯定是边缘;小于 t1 的点肯定不是边缘;在 t1, t2 之间的点,通过已确定的边缘点,发起8领域方向的搜索(广搜),图中可达的是边缘,不可达的点不是边缘。最后得出 canny 边缘图。
(2)二阶导算子
1、lapacian
一阶差分:f '(x) = f(x) - f(x - 1)
二阶差分:f '(x) = (f(x + 1) - f(x)) - (f(x) - f(x - 1))
化简后:f '(x) = f(x - 1) - 2 f(x)) + f(x + 1)
提取前面的系数:[1, -2, 1]
二维的情况下,同理可得f '(x, y) = -4 f(x, y) + f(x-1, y) + f(x+1, y) + f(x, y-1) + f(x, y+1)提取各个系数,写成模板的形式
0, 1, 0
1, -4, 1
0, 1, 0
考虑两个斜对角的情况
1, 1, 1
1, -8, 1
1, 1, 1
与原图卷积运算即可求出边缘。
那么这些算子有什么区别呢:
下面三张图分别是 sobel,canny,laplace 结果图。
sobel 产生的边缘有强弱,抗噪性好,计算量小
laplace 对边缘敏感,可能有些是噪声的边缘,也被算进来了
canny 产生的边缘很细,可能就一个像素那么细,没有强弱之分。计算量大,但是准确
部分参考自:https://www.jianshu.com/p/2334bee37de5
常见边缘检测对比(Roberts算子Prewitt算子Sobel算子Laplacian算子Canny算子)
目录
方法对比
 算子:基于一阶导数的方法
算子:基于一阶导数的方法 算子:基于一阶导数的方法
算子:基于一阶导数的方法 算子:基于一阶导数的方法
算子:基于一阶导数的方法 算子:基于二阶导数的方法
算子:基于二阶导数的方法 算子:非微分边缘检测算子
算子:非微分边缘检测算子
公式对比
 算子:
算子: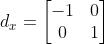 ,
,
 算子:
算子: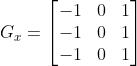 ,
,
 算子:
算子: ,
,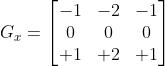
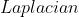 算子:
算子: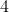 领域:
领域: ;
; 邻域:
邻域:
 算子:实现步骤:1. 用高斯滤波器平滑图像
算子:实现步骤:1. 用高斯滤波器平滑图像
2. 计算图像中每个像素点的梯度强度和方向
3. 对梯度幅值进行非极大值抑制
4. 用双阈值算法检测来确定真实和潜在的边缘
优点对比
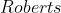 算子:对垂直边缘的检测效果好于斜向边缘
算子:对垂直边缘的检测效果好于斜向边缘
对具有陡峭的低噪声的图像效果最好
定位精度高 算子:边缘检测结果在水平方向和垂直方向均比
算子:边缘检测结果在水平方向和垂直方向均比  算子明显
算子明显
适合用来识别噪声较多,灰度渐变的图像
对噪声有抑制作用,抑制噪声的原理是通过像素平均 算子:
算子: 算子要比
算子要比  算子更能准确检测图像边缘
算子更能准确检测图像边缘
边缘定位较准确,常用于噪声较多,灰度渐变的图像
对像素位置的影响做了加权,相比之下比 算子、
算子、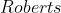 算子效果更好
算子效果更好
以滤波算子的形式来提取边缘,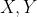 方向各用一个模板,两个模板组合起来构成一个梯度算子。
方向各用一个模板,两个模板组合起来构成一个梯度算子。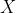 方向模板对垂直边缘影响最大,
方向模板对垂直边缘影响最大,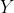 方向模板对水平边缘影响最大。
方向模板对水平边缘影响最大。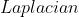 算子:对图像中的阶跃性边缘点定位准确
算子:对图像中的阶跃性边缘点定位准确 算子:对噪声不敏感,不容易受到噪声干扰
算子:对噪声不敏感,不容易受到噪声干扰
能够检测到真正的弱边缘
使用两种不同的阈值分别检测强边缘和弱边缘
仅当强边缘与弱边缘相连时才将弱边缘包含在输出图像中
缺点对比
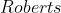 算子:对噪声敏感,无法抑制噪声的影响
算子:对噪声敏感,无法抑制噪声的影响
提取边缘的结果是边缘比较粗
边缘定位不是很准确 算子:像素平均相当于对图像的低通滤波,所以
算子:像素平均相当于对图像的低通滤波,所以  算子对边缘的定位不如
算子对边缘的定位不如 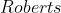 算子
算子 算子:由于边缘是位置的标志,对灰度的变化不敏感
算子:由于边缘是位置的标志,对灰度的变化不敏感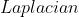 算子:对噪声比较敏感,只适用于无噪声图像
算子:对噪声比较敏感,只适用于无噪声图像
容易丢失边缘方向信息,造成一些不连续的检测边缘 算子:易使高频边缘被平滑掉,从而造成边缘丢失
算子:易使高频边缘被平滑掉,从而造成边缘丢失
常用场景对比
-
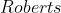 算子:常用于垂直边缘明显或具有陡峭的低噪声的图像的边缘检测任务
算子:常用于垂直边缘明显或具有陡峭的低噪声的图像的边缘检测任务  算子:常用于噪声较多、灰度渐变的图像的边缘检测任务
算子:常用于噪声较多、灰度渐变的图像的边缘检测任务 算子:常用于噪声较多,灰度渐变的图像的边缘检测任务
算子:常用于噪声较多,灰度渐变的图像的边缘检测任务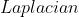 算子:常用于归一化检测结果,进行方差计算,可以用在模糊检测任务上
算子:常用于归一化检测结果,进行方差计算,可以用在模糊检测任务上 算子:被用于诸如“车道线检测”等实际项目中,是最有效的边缘检测方法
算子:被用于诸如“车道线检测”等实际项目中,是最有效的边缘检测方法
边缘检测结果对比
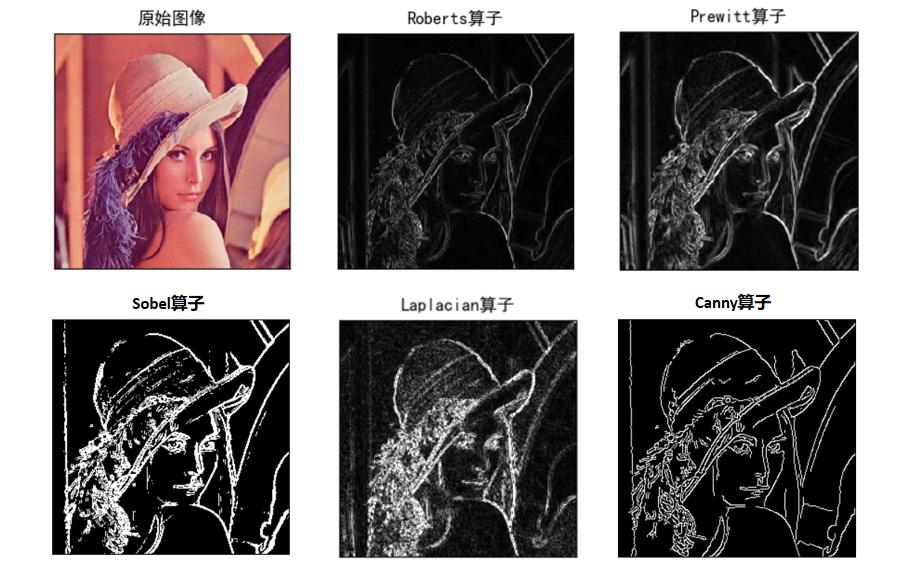
END
以上是关于图像边缘检测:Canny算子、Prewitt算子和sobel算子的主要内容,如果未能解决你的问题,请参考以下文章
常见边缘检测对比(Roberts算子Prewitt算子Sobel算子Laplacian算子Canny算子)
常见边缘检测对比(Roberts算子Prewitt算子Sobel算子Laplacian算子Canny算子)