PyTorch学习笔记 8. 实现线性回归模型

Posted 2023-03-18

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了PyTorch学习笔记 8. 实现线性回归模型相关的知识，希望对你有一定的参考价值。

PyTorch学习笔记 8. 实现线性回归模型

一、回归的概念

1. 概念
2. 目标
3. 应用
4. 训练线性回归的步骤

二、数据集

1. 构造数据集
2. 把数据集转为 pytorch 使用的张量

三、模型

1. 模型定义
2. 损失函数
3. 优化器

四、使用模型

1. 训练
2. 测试
3. 预测
4. 可视化

五、完整代码实现

PyTorch学习笔记

一、回归的概念

1. 概念

回归（Linear Regression）是一种基本的统计学习方法，它用于建立两个或多个变量之间的关系。

线性回归假设自变量（输入）和因变量（输出）之间是线性关系，即输出值可以通过一条直线（或超平面）来表示输入值的函数。
逻辑回归拟合的结果是非线性关系，也称为广义线性回归。

回归问题与分类问题的区别：

回归问题中，预测值是连续值；
分类问题中，预测值是离散值。

2. 目标

线性回归的目标是找到一条最佳拟合直线，以最小化预测值与实际值之间的差距（误差）。

3. 应用

线性回归在机器学习和数据分析中被广泛使用，它可以用于预测、分类和特征选择等任务。它的应用领域包括金融、经济学、社会科学、医学和工程学等领域。

4. 训练线性回归的步骤

定义网络模型：包括神经网络的层数、每一层的神经元数、激活函数等。
定义损失函数：根据问题的性质，选择适合的损失函数。
定义优化器：选择合适的优化器来更新神经网络的参数，如SGD、Adam等。
遍历训练数据：对于每个训练样本，进行前向传播，计算损失函数，并进行反向传播求梯度。
更新网络参数：根据梯度信息和优化器的选择，更新神经网络的参数。
重复上述步骤，直到达到预设的停止条件，如训练次数达到上限、损失函数下降到一定程度等。

训练的过程中要避免过拟合现象，可采用一些方法如早停法、正则化等来缓解。

二、数据集

1. 构造数据集

本例定义一个 PyTorch学习笔记

np.random.seed(0)
x_train = np.random.rand(100, 1)

y_train = 5 * x_train + 2 + 0.2 * np.random.randn(100, 1)
x_test = np.random.rand(20, 1)
y_test = 5 * x_test + 2 + 0.2 * np.random.randn(20, 1)

2. 把数据集转为 pytorch 使用的张量

x_train_tensor = torch.from_numpy(x_train).float()
y_train_tensor = torch.from_numpy(y_train).float()
x_test_tensor = torch.from_numpy(x_test).float()
y_test_tensor = torch.from_numpy(y_test).float()

三、模型

1. 模型定义

为了实现线性回归，我们定义只有一个层的神经网络LinearRegression，在类中定义了一个全连接层linear，这个层的输入和输出都是1维的。

在前向传播方法中，输入x被传入全连接层中进行计算，得到模型的输出out，然后将其返回。

模型的输出out就是输入x的线性变换结果，具体的计算公式为 PyTorch学习笔记，其中是全连接层的权重，是偏置，由于输入和输出都是1维的，因此也是一个1维的向量，是一个标量。

# 定义模型
class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(1, 1)

    def forward(self, x):
        out = self.linear(x)
        return out

2. 损失函数

线性回归使用均方误差损失函数。
均方误差损失函数，又称为平方损失函数，是一种用于回归问题的损失函数，计算预测值与真实值之间差异的平方和。在训练过程中，通过不断调整模型参数，最小化损失函数，使得模型能够更好地拟合训练数据。

均方误差损失函数容易受到噪声的影响，不适用于离群点数据。

criterion = nn.MSELoss()

3. 优化器

这里使用了 torch.optim.SGD优化器，即随机梯度下降优化器（Stochastic Gradient Descent Optimizer），其通过对模型参数的梯度进行迭代更新，来最小化损失函数。

SGD是深度学习中最常用的优化器之一，也是最基础的优化器之一。

lr 表示学习率，它控制了优化器每次更新参数的步长大小。

较小的学习率会使优化器收敛缓慢，但是可能会得到更准确的结果；
较大的学习率会使优化器收敛较快，但是可能会错过最优解。
选择学习率的大小需要根据具体问题进行调整。在下面的代码中，学习率被设置为 0.01，这个值是一个经验值，通常需要根据实际情况进行调整。

optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

四、使用模型

1. 训练

这里重点是反向传播。
通过计算损失函数对模型参数的梯度，可以确定当前参数下损失函数变化最快的方向，然后将参数朝着这个方向更新，以期望能够使损失函数的值减小。

计算反向传播的一般步骤是：

通过前向传播计算模型输出；
计算损失函数；
计算损失函数对模型参数的梯度；
使用计算得到的梯度对模型参数进行更新。

在每次计算梯度时，要注意梯度的值会累加到模型参数的梯度值中，因此需要在每个batch或每个epoch开始之前将模型参数的梯度值清零。如果不清零，梯度值会一直累加并影响到后续梯度的计算，导致训练出现问题。

# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    # 前向传播
    y_pred = model(x_train_tensor)
    # 计算损失
    loss = criterion(y_pred, y_train_tensor)
    # 反向传播和优化
    # 清除所有模型参数的梯度值
    optimizer.zero_grad()
    # 计算损失函数对模型参数的梯度
    loss.backward()
    # 根据计算出的梯度更新模型参数
    optimizer.step()
    # 每隔50个epoch输出一次信息
    if (epoch + 1) % 50 == 0:
        print(Epoch[/], loss: :.6f.format(epoch + 1, num_epochs, loss.item()))

2. 测试

查看损失：
在PyTorch中，损失函数计算的结果一般会返回一个tensor，这个tensor里面存储的是所有样本的损失值，如果要在训练过程中及时查看损失函数的值，需要将这个tensor转换成Python标量（即一个float数值），通过调用item()方法实现。这样得到的就是单个数值，便于进行打印输出、可视化等操作。

# 测试模型
model.eval（)
with torch.no_grad():
    y_pred_train = model(x_train_tensor)
    y_pred_test = model(x_test_tensor)
train_loss = criterion(y_pred_train, y_train_tensor).item()
test_loss = criterion(y_pred_test, y_test_tensor).item()
print(fTrain loss: train_loss:.6f, Test loss: test_loss:.6f)

3. 预测

# 预测结果
x_new_tensor = torch.Tensor([[0.2], [0.4], [0.6]])
y_new_tensor = model(x_new_tensor).detach().numpy()
print(fPrediction for x_new_tensor: y_new_tensor)

4. 可视化

可视化时，把预测结果转换成 numpy 数组，并且使用 detach() 方法将其与计算图分离，即使其不参与反向传播；最后使用matplotlib绘制函数。

# 可视化结果
model.eval（)
y_pred = model(x_train_tensor).detach().numpy()
plt.plot(x_train_tensor.numpy(), y_train_tensor.numpy(), ro, label=Original data)
plt.plot(x_train_tensor.numpy(), y_pred, label=Fitted line)
plt.legend()
plt.show()

五、完整代码实现

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt

# 生成随机数据
np.random.seed(0)
x_train = np.random.rand(100, 1)
y_train = 5 * x_train + 2 + 0.2 * np.random.randn(100, 1)
x_test = np.random.rand(20, 1)
y_test = 5 * x_test + 2 + 0.2 * np.random.randn(20, 1)

# 转换为张量
x_train_tensor = torch.from_numpy(x_train).float()
y_train_tensor = torch.from_numpy(y_train).float()
x_test_tensor = torch.from_numpy(x_test).float()
y_test_tensor = torch.from_numpy(y_test).float()


# 定义模型
class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(1, 1)

    def forward(self, x):
        out = self.linear(x)
        return out


model = LinearRegression()

# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    # 前向传播
    y_pred = model(x_train_tensor)
    # 计算损失
    loss = criterion(y_pred, y_train_tensor)
    # 反向传播和优化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    # 每隔50个epoch输出一次信息
    if (epoch + 1) % 50 == 0:
        print(Epoch[/], loss: :.6f.format(epoch + 1, num_epochs, loss.item()))


# 测试模型
model.eval（)
with torch.no_grad():
    y_pred_train = model(x_train_tensor)
    y_pred_test = model(x_test_tensor)
train_loss = criterion(y_pred_train, y_train_tensor).item()
test_loss = criterion(y_pred_test, y_test_tensor).item()
print(fTrain loss: train_loss:.6f, Test loss: test_loss:.6f)


# 预测结果
x_new_tensor = torch.Tensor([[0.2], [0.4], [0.6]])
y_new_tensor = model(x_new_tensor).detach().numpy()
print(fPrediction for x_new_tensor: y_new_tensor)


# 可视化结果
model.eval（)
y_pred = model(x_train_tensor).detach().numpy()
plt.plot(x_train_tensor.numpy(), y_train_tensor.numpy(), ro, label=Original data)
plt.plot(x_train_tensor.numpy(), y_pred, label=Fitted line)
plt.legend()
plt.show()

可视化结果：

PyTorch学习笔记

《动手学深度学习》softmax回归(PyTorch版)

前几节介绍的线性回归模型适用于输出为连续值的情景。在另一类情景中，模型输出可以是一个像图像类别这样的离散值。

对于这样的离散值预测问题，我们可以使用诸如softmax回归在内的分类模型。和线性回归不同，softmax回归的输出单元从一个变成了多个，且引入了softmax运算使输出更适合离散值的预测和训练。本节以softmax回归模型为例，介绍神经网络中的分类模型。

1 分类问题

让我们考虑一个简单的图像分类问题，其输入图像的高和宽均为2像素，且色彩为灰度。这样每个像素值都可以用一个标量表示。我们将图像中的4像素分别记为 $x_1, x_2, x_3, x_4$ 。假设训练数据集中图像的真实标签为狗、猫或鸡（假设可以用4像素表示出这3种动物），这些标签分别对应离散值 $y_1, y_2, y_3$ 。

我们通常使用离散的数值来表示类别，例如 $y_1=1, y_2=2, y_3=3$ 。如此，一张图像的标签为1、2和3这3个数值中的一个。

虽然我们仍然可以使用回归模型来进行建模，并将预测值就近定点化到1、2和3这3个离散值之一，但这种连续值到离散值的转化通常会影响到分类质量。因此我们一般使用更加适合离散值输出的模型来解决分类问题。

2 softmax回归模型

softmax回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于，softmax回归的输出值个数等于标签里的类别数。因为一共有4种特征和3种输出动物类别，所以权重包含12个标量（带下标的 $w$ ）、偏差包含3个标量（带下标的 $b$ ），且对每个输入计算 $o_1, o_2, o_3$ 这3个输出：

$\\begin{aligned} o_1 &= x_1 w_{11} + x_2 w_{21} + x_3 w_{31} + x_4 w_{41} + b_1,\\\\ o_2 &= x_1 w_{12} + x_2 w_{22} + x_3 w_{32} + x_4 w_{42} + b_2,\\\\ o_3 &= x_1 w_{13} + x_2 w_{23} + x_3 w_{33} + x_4 w_{43} + b_3. \\end{aligned}$

图3.2用神经网络图描绘了上面的计算。softmax回归同线性回归一样，也是一个单层神经网络。

由于每个输出 $o_1, o_2, o_3$ 的计算都要依赖于所有的输入 $x_1, x_2, x_3, x_4$ ，softmax回归的输出层也是一个全连接层。

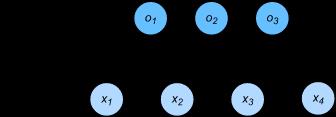
图3.2 softmax回归是一个单层神经网络

既然分类问题需要得到离散的预测输出，一个简单的办法是将输出值 $o_i$ 当作预测类别是 $i$ 的置信度，并将值最大的输出所对应的类作为预测输出，即输出 $\\underset{i}{\\arg\\max} o_i$ 。例如，如果 $o_1,o_2,o_3$ 分别为 $0.1, 10, 0.1$ ，由于 $o_2$ 最大，那么预测类别为2，其代表猫。

然而，直接使用输出层的输出有两个问题。一方面，由于输出层的输出值的范围不确定，我们难以直观上判断这些值的意义。例如，刚才举的例子中的输出值10表示“很置信”图像类别为猫，因为该输出值是其他两类的输出值的100倍。但如果 $o_1=o_3=10^3$ ，那么输出值10却又表示图像类别为猫的概率很低。另一方面，由于真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量。

softmax运算符（softmax operator）解决了以上两个问题。它通过下式将输出值变换成值为正且和为1的概率分布：

$\\hat{y}_1, \\hat{y}_2, \\hat{y}_3 = \\text{softmax}(o_1, o_2, o_3)$

《动手学深度学习》线性回归的简洁实现（linear-regression-pytorch）

[深度学习][pytorch]pytorch实现一个简单得线性回归模型并训练

pytorch学习笔记：线性回归（用pytorchAPI）

Pytorch 线性回归损失增加

PyTorch学习笔记 8. 实现线性回归模型

PyTorch学习笔记 8. 实现线性回归模型

一、 回归的概念

1. 概念

2. 目标

3. 应用

4. 训练线性回归的步骤

二、数据集

1. 构造数据集

2. 把数据集转为 pytorch 使用的张量

三、模型

1. 模型定义

2. 损失函数

3. 优化器

四、使用模型

1. 训练

2. 测试

3. 预测

4. 可视化

五、完整代码实现

《动手学深度学习》softmax回归(PyTorch版)

softmax-regression

1 分类问题

2 softmax回归模型

一、回归的概念