急！！！单纯形法为啥叫这个名字？？？帮帮忙啊

Posted 2023-03-16

不是问原理，只是想知道这个名字是怎么来的，谢谢

参考技术A 单纯形法的发明人——Dantzig
1914-2005

Dantzig, the inventor of the Simplex Method and, with Philip Wolfe, the Decomposition Principle for large linear-programming problems, which together made linear programming computationally viable, died in Stanford on May 13th.

The son of a mathematician, George Bernard Dantzig was born in Portland, Oregon on November 8, 1914. His father, Tobias Dantzig, had been born in Latvia but, after being caught distributing anti-Tsarist propaganda, fled to Paris, where he studied under Henri Poincar?and met Anja Ourisson, then at the Sorbonne. They married and emigrated to Oregon, where Dantzig took jobs as a lumberjack and navvy.
Though the family was initially very poor, Tobias Dantzig had ambitions for his children: George was named after George Bernard Shaw in the hope that he would become a writer, while his younger brother Henry took his name from Poincar? and did in fact become a mathematician. Tobias Dantzig eventually took a PhD at the University of Indiana, and his wife, after taking a degree in French, became a linguist at the Library of Congress in Washington DC.

George Dantzig received degrees from Maryland (1936) and the University of Michigan before earning his doctorate from the University of California, Berkeley, in 1946. While at Berkeley, he made an immediate impact (as described by Dr. Dantzig).

During my first year at Berkeley I arrived late one day to one of [Jerzy] Neyman's classes. On the blackboard were two problems which I assumed had been assigned for homework. I copied them down. A few days later I apologised to Neyman for taking so long to do the homework - the problems seemed to be a little harder than usual. I asked him if he still wanted the work. He told me to throw it on his desk?
About six weeks later, one Sunday morning about eight o'clock, Anne and I were awakened by someone banging on our front door. It was Neyman. He rushed in with papers in hand, all excited: 'I've just written an introduction to one of your papers. Read it so I can send it out right away for publication.' For a minute I had no idea what he was talking about. To make a long story short, the problems on the blackboard which I had solved thinking they were homework were in fact two famous unsolved problems in statistics. That was the first inkling I had that there was anything special about them.

George Dantzig worked for the US Bureau of Labor Statistics, served as Chief of the Combat Analysis Branch for USAF Headquarters Statistical Control and as Mathematical Advisor for USAF Headquarters, Research Mathematician for RAND Corporation, and Professor of Operations Research and Chairman of the Operations Research Center at the University of California, Berkeley.

While making calculations for the Air Force in 1947, Dr. Dantzig developed the simplex algorithm to facilitate programming (military jargon for planning, rather than today's computer use) in a linear structure. This enabled mathematicians, economists and others to consider large numbers of variables in broad-reaching decisions about the production and allocation of airplanes, their parts and raw materials.

The field that resulted, called linear programming, has been applied subsequently to utilities, oil refineries, investments and the steel industry to aid in planning and efficiency under uncertain conditions. It has also been used to prepare cost-effective nutritional diets and coordinate the routes of commercial aircraft. Dantzig confessed to being surprised by the "tremendous power" of his method, which he explored in computing after his move to the Rand corporation in 1952.

In the 1950's and 60's, Dr. Dantzig broadened his simplex method to economic models, to reduce paper waste in the printing industry and to other problems of applied mathematics. With another researcher, Philip Wolfe, he developed the Dantzig-Wolfe decomposition principle, which is intended to simplify oversized problems in planning and logistics involving vast amounts of data.

In 1960, he became a professor of operations research at Berkeley. He moved to Stanford in 1966 and continued to teach and publish into the 1990's as a Professor of Operations Research and Computer Science, Co-Director of the Systems Optimization Laboratory, and Director of the PILOT Energy-Economic Model Project.

Dr. Dantzig's other interests included game theory, quadratic programming and a means of studying problems that involve significant uncertainty, known as stochastic programming.

Professor Dantzig's seminal work has laid the foundation for much of the field of systems engineering and is widely used in network design and component design in computer, mechanical, and electrical engineering.

Dr. Dantzig was a member of the National Academy of Engineering, the National Academy of Science, the American Academy of Arts and Sciences and recipient of the National Medal of Science, plus eight honorary degrees. He served at the thirteenth president of TIMS (one of the societies that merged to form INFORMS) and won the first ORSA/TIMS von Neumann Theory Prize, the National Medal of Science and the Hervey prize.

His work inspired the formation of the Mathematical Programming Society, a major section of the Society for industrial and applied mathematics, and numerous professional and academic bodies. Generations of Professor Dantzig's students have become the leaders in all facets of society.

Dr. Dantzig died on May 13, 2005 of complications from diabetes and heart disease.

: Though the family was initially very poor, Tobias Dantzig had ambitions for his children: George was named after George Bernard Shaw in the hope that he would become a writer, while his younger brother Henry took his name from Poincar? and did in fac
: George Dantzig received degrees from Maryland (1936) and the University of Michigan before earning his doctorate from the University of California, Berkeley, in 1946. While at Berkeley, he made an immediate impact (as described by Dr. Dantzig).
: During my first year at Berkeley I arrived late one day to one of [Jerzy] Neyman's classes. On the blackboard were two problems which I assumed had been assigned for homework. I copied them down. A few days later I apologised to Neyman for taking so
: About six weeks later, one Sunday morning about eight o'clock, Anne and I were awakened by someone banging on our front door. It was Neyman. He rushed in with papers in hand, all excited: 'I've just written an introduction to one of your papers. Read
: George Dantzig worked for the US Bureau of Labor Statistics, served as Chief of the Combat Analysis Branch for USAF Headquarters Statistical Control and as Mathematical Advisor for USAF Headquarters, Research Mathematician for RAND Corporation, and P
: While making calculations for the Air Force in 1947, Dr. Dantzig developed the simplex algorithm to facilitate programming (military jargon for planning, rather than today's computer use) in a linear structure. This enabled mathematicians, economists
: ...................

单纯形法剖析，一句话描述单纯形法

一句话描述单纯形法：

从可行域的一个顶点跳到另一个顶点，使得目标函数改善的过程。直到满足终止条件。

解释一下这句话

可行域的顶点？其实就是所谓的基可行解

终止条件，其实就是所谓的检验数全为非正。

这儿得注意，检验数有为0的意味着可能存在无穷多个最优解，即在两个顶点连线上的点都是最优，还有一个就是无有限解，解无穷大，这个的判断是在进基时发现这个基对应的约束系数（这儿的系数是我们变换了的，不是最开始的啊）全是负的

问题来了？

1、第一个顶点（基可行解）怎么产生？

答：有的问题可以直接看出约束的系数矩阵里面有单位阵，有的则不好看出来或者看不出来。那么用大M法，或者两阶段法产生一个基可行解，如果产生不了，说明无解。

这个大M法和两阶段法自己去看。

2、你说从一个顶点跳到另一个顶点？怎么跳？

答：这就是所谓的进基的出基，目的是从一个基可行解得到另一个基可行解。

3、进基与出基，我该进那个出那个呢？

答：进基一般进检验数最大的那个（也有按顺序对检验数大于0的进基），出基其实不是你决定的，它决定于你进基的是那个，因为我们进基肯定把这个基最大的来进，举个列子

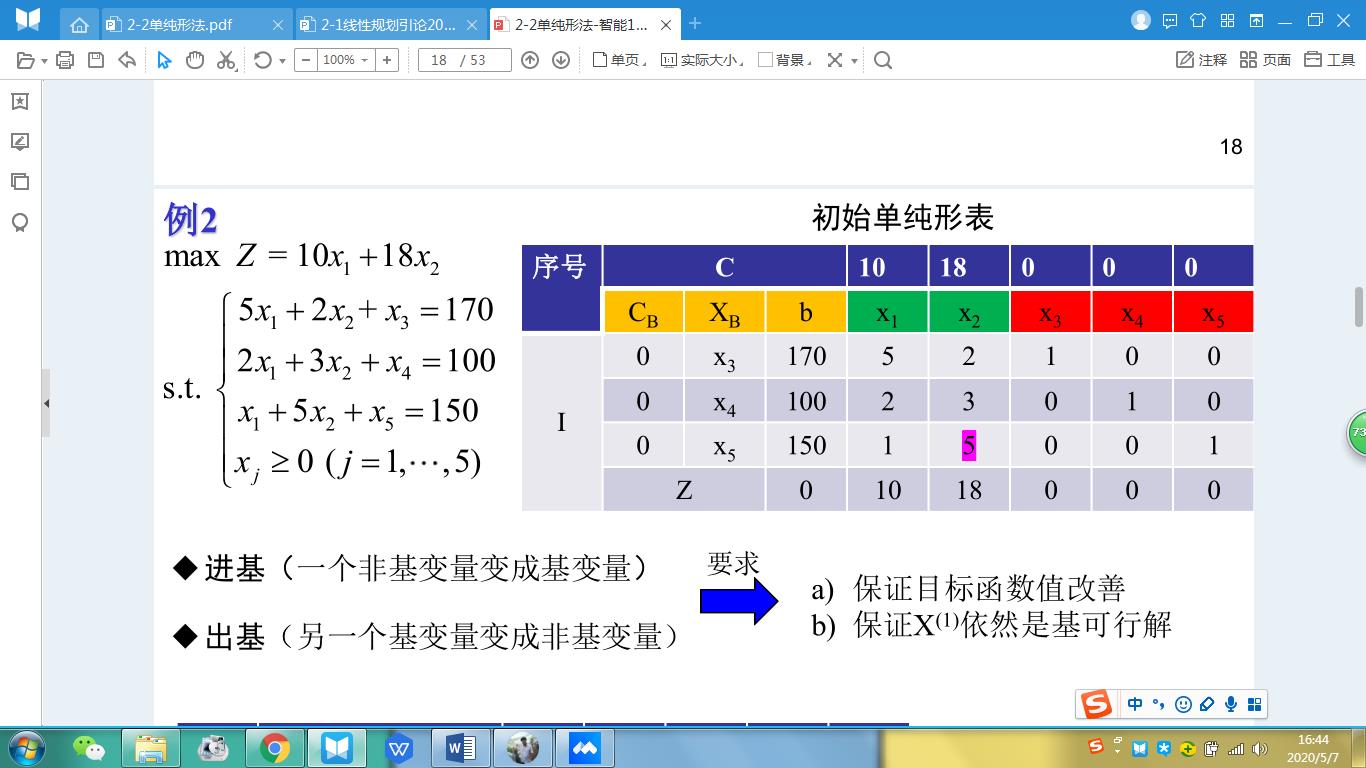
这张图最开始的基是x{3,4,5}，我们进基，18>10，所以我们肯定是进x2。进多少呢？
第一个约束最大允许我们进85，第二个100/3，第三个30.显然我们要满足所有约束，那么就是进30，自然而然，出基的就是第三个约束中的x5。所以说你进基的元素决定了你出基的元素

过程如下

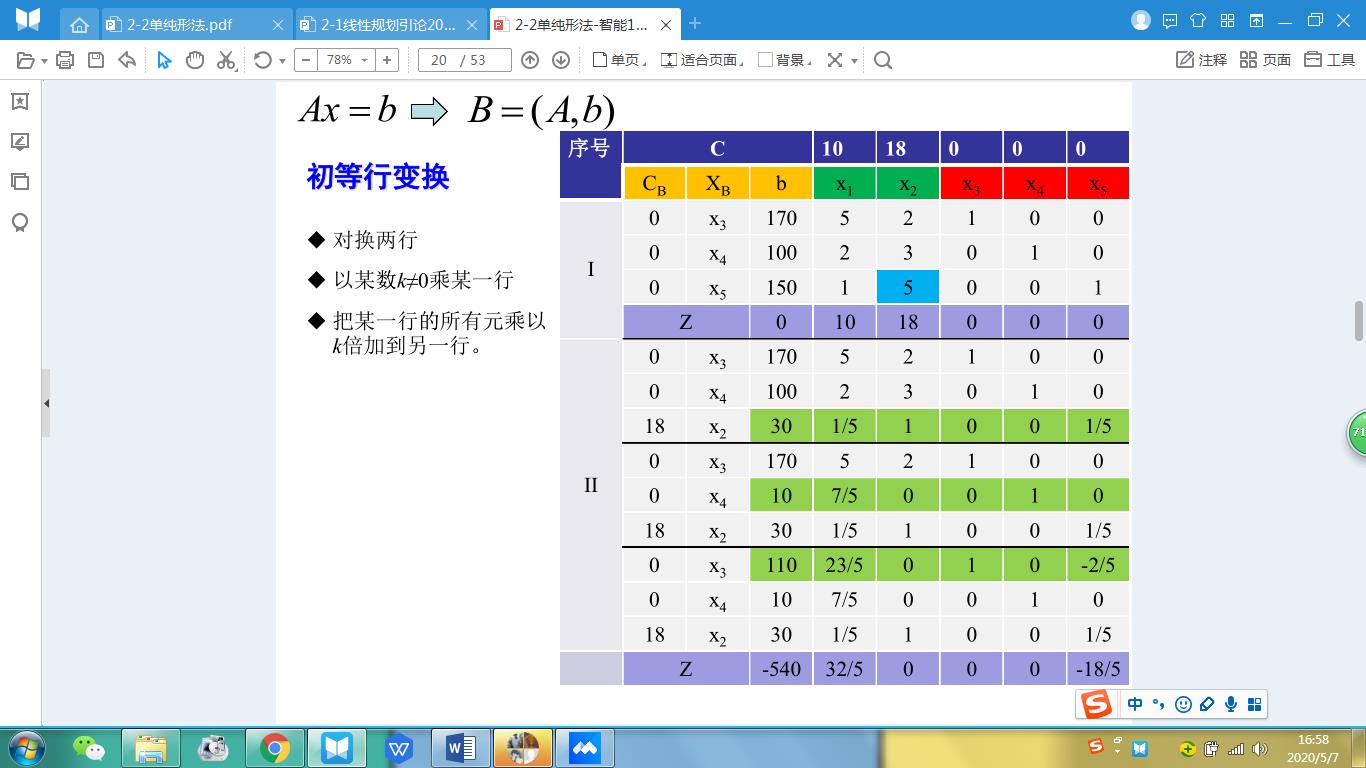
4、好的，现在我进基完了，也用非基变量表示我的目标函数了，我接下来是继续进基呢，还是停止？

答：看是否满足终止条件 1、所有的检验数为负吗? 是的，那么恭喜，找到了最优解。
2、检验数里面没有正的但是有0？是的，那么说明最优解有无穷多个，即在两个顶点连线上的点都是最优解。上述两个情况都不是，进基。

刚刚第三个问题没说，在进基时要判断进的这个基是不是约束系数都小于0了，全小于0的话说明这个问题没有有限最优解，也就是说最优解无穷大。

也很容易理解啊，如果全为负，我们又是等式约束，我们说了希望进基最大，那么我把这个基进无穷大，负的系数乘以无穷大是无穷小，肯定在我的等式约束内，这样一来我们的基可行解（顶点）的某个坐标不就跑到无穷去了吗，那可不就是没有有限最优解嘛。