回溯法与分支限界
Posted 松子茶
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了回溯法与分支限界相关的知识,希望对你有一定的参考价值。
回溯法
1、有许多问题,当需要找出它的解集或者要求回答什么解是满足某些约束条件的最佳解时,往往要使用回溯法。
2、回溯法的基本做法是搜索,或是一种组织得井井有条的,能避免不必要搜索的穷举式搜索法。这种方法适用于解一些组合数相当大的问题。
3、回溯法在问题的解空间树中,按深度优先策略,从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时,先判断该结点是否包含问题的解。如果肯定不包含(剪枝过程),则跳过对该结点为根的子树的搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先策略搜索。
问题的解空间
问题的解向量:回溯法希望一个问题的解能够表示成一个n元式(x1,x2,…,xn)的形式。
显约束:对分量xi的取值限定。
隐约束:为满足问题的解而对不同分量之间施加的约束。
解空间:对于问题的一个实例,解向量满足显式约束条件的所有多元组,构成了该实例的一个解空间。
注意:同一个问题可以有多种表示,有些表示方法更简单,所需表示的状态空间更小(存储量少,搜索方法简单)。
下面是n=3时的0-1背包问题用完全二叉树表示的解空间:
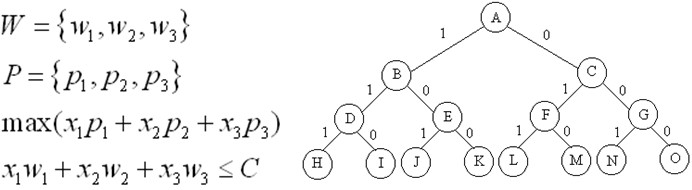
生成问题状态的基本方法
扩展结点:一个正在产生儿子的结点称为扩展结点
活结点:一个自身已生成但其儿子还没有全部生成的节点称做活结点
死结点:一个所有儿子已经产生的结点称做死结点
深度优先的问题状态生成法:如果对一个扩展结点R,一旦产生了它的一个儿子C,就把C当做新的扩展结点。在完成对子树C(以C为根的子树)的穷尽搜索之后,将R重新变成扩展结点,继续生成R的下一个儿子(如果存在)
宽度优先的问题状态生成法:在一个扩展结点变成死结点之前,它一直是扩展结点
回溯法:为了避免生成那些不可能产生最佳解的问题状态,要不断地利用限界函数(bounding function)来处死(剪枝)那些实际上不可能产生所需解的活结点,以减少问题的计算量。具有限界函数的深度优先生成法称为回溯法。(回溯法 = 穷举 + 剪枝)
回溯法的基本思想
(1)针对所给问题,定义问题的解空间;
(2)确定易于搜索的解空间结构;
(3)以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
两个常用的剪枝函数:
- (1)约束函数:在扩展结点处减去不满足约束的子数
- (2)限界函数:减去得不到最优解的子树
用回溯法解题的一个显著特征是在搜索过程中动态产生问题的解空间。在任何时刻,算法只保存从根结点到当前扩展结点的路径。如果解空间树中从根结点到叶结点的最长路径的长度为h(n),则回溯法所需的计算空间通常为O(h(n))。而显式地存储整个解空间则需要 O(2h(n)) 或O(h(n)!)内存空间。
回溯算法的设计步骤
回溯算法的递归实现和迭代实现
递归回溯
回溯法对解空间作深度优先搜索,因此,在一般情况下用递归方法实现回溯法。
// 针对N叉树的递归回溯方法
void backtrack (int t)
if (t > n)
// 到达叶子结点,将结果输出
output (x);
else
// 遍历结点t的所有子结点
for (int i = f(n,t); i <= g(n,t); i ++ )
x[t] = h[i];
// 如果不满足剪枝条件,则继续遍历
if (constraint (t) && bound (t))
backtrack (t + 1);
迭代回溯
采用树的非递归深度优先遍历算法,可将回溯法表示为一个非递归迭代过程。
// 针对N叉树的迭代回溯方法
void iterativeBacktrack ()
int t = 1;
while (t > 0)
if (f(n,t) <= g(n,t))
// 遍历结点t的所有子结点
for (int i = f(n,t); i <= g(n,t); i ++)
x[t] = h(i);
// 剪枝
if (constraint(t) && bound(t))
// 找到问题的解,输出结果
if (solution(t))
output(x);
else // 未找到,向更深层次遍历
t ++;
else
t--;
回溯法一般依赖的两种数据结构:子集树和排列树
子集树(遍历子集树需
O(2n)
计算时间)

void backtrack (int t)
if (t > n)
// 到达叶子结点
output (x);
else
for (int i = 0;i <= 1;i ++)
x[t] = i;
// 约束函数
if ( legal(t) )
backtrack( t+1 );
排列树(遍历排列树需要O(n!)计算时间)
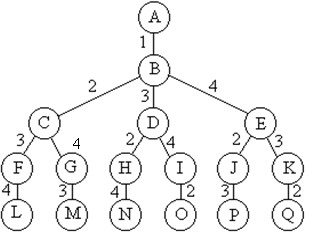
void backtrack (int t)
if (t > n)
output(x);
else
for (int i = t;i <= n;i++)
// 完成全排列
swap(x[t], x[i]);
if (legal(t))
backtrack(t+1);
swap(x[t], x[i]);
几个典型的例子
装载问题
问题表述:有一批共n个集装箱要装上2艘载重量分别为c1和c2的轮船,其中集装箱i的重量为wi,且
∑ni=1wi≤c1+c2
装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。如果有,找出一种装载方案。
解决方案:
容易证明,如果一个给定装载问题有解,则采用下面的策略可得到最优装载方案。
(1)首先将第一艘轮船尽可能装满;
(2)将剩余的集装箱装上第二艘轮船。
将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集,使该子集中集装箱重量之和最接近。由此可知,装载问题等价于以下特殊的0-1背包问题。
解空间:
子集树可行性约束函数(选择当前元素):
上界函数(不选择当前元素):
void backtrack (int i)
// 搜索第i层结点
if (i > n) // 到达叶结点
更新最优解bestx,bestw;return;
r -= w[i];
if (cw + w[i] <= c)
// 搜索左子树
x[i] = 1;
cw += w[i];
backtrack (i + 1);
cw -= w[i];
if (cw + r > bestw)
x[i] = 0; // 搜索右子树
backtrack(i + 1);
r += w[i];
变量解释:
r: 剩余重量
w: 各个集装箱重
cw:当前总重量
x: 每个集装箱是否被选取标志
bestx: 最佳选取方案
bestw: 最优载重量
实现:
#include <iostream>
#include <vector>
#include <iterator>
using namespace std;
/* 装载问题子函数
* layers: 搜索到第layers层结点
* layers_size: layers_size总层数
* current_w: 当前承载量
* best_w: 最优载重量
* flag_x: 选取方案
* best_x: 最佳选取方案
* remainder_w:剩余重量
* container_w:每个集装箱的重量
* total_w: 总承载量
*/
void __backtrack (int layers,const int layers_size,
int current_w,int& best_w,
vector<int>& flag_x,vector<int>&
best_x,
int remainder_w,
const vector<int>& container_w,
int total_w)
if (layers > layers_size - 1)
// 到达叶子结点,更新最优载重量
if (current_w < best_w || best_w == -1)
copy(flag_x.begin(),flag_x.end
(),best_x.begin());
// copy(best_x.begin(),best_x.end
(),flag_x.begin());
best_w = current_w;
return;
remainder_w -= container_w[layers];
if (current_w + container_w[layers] <= total_w)
// 搜索左子树
flag_x[layers] = 1;
current_w += container_w[layers];
__backtrack(layers + 1,layers_size,current_w,
best_w,flag_x,best_x,remainder_w,container_w,
total_w);
current_w -= container_w[layers];
if (current_w + remainder_w > best_w || best_w == -
1)
flag_x[layers] = 0;
__backtrack(layers + 1,layers_size,current_w,
best_w,flag_x,best_x,remainder_w,container_w,
total_w);
remainder_w += container_w[layers];
/* 装载问题
* container_w: 各个集装箱重量
* total_w: 总承载量
*/
void loading_backtrack (int total_w, vector<int>&
container_w)
int layers_size = container_w.size(); // 层数
int current_w = 0; // 当前装载重量
int remainder_w = total_w; // 剩余重量
int best_w = -1; // 最优载重量
vector<int> flag_x(layers_size); // 是否被选取标
志
vector<int> best_x(layers_size); // 最佳选取方案
__backtrack(0,layers_size,current_w,
best_w,flag_x,best_x,remainder_w,container_w,
total_w);
cout << "path : " ;
copy(best_x.begin(),best_x.end
(),ostream_iterator<int>(cout," "));
cout << endl;
cout << "best_w = " << best_w
<< "( ";
// 将结果输出
for (size_t i = 0;i < best_x.size(); ++ i)
if (best_x[i] == 1)
cout << container_w[i] << " ";
cout << ")" << endl;
int main()
const int total_w = 30;
vector<int> container_w;
container_w.push_back(40);
container_w.push_back(1);
container_w.push_back(40);
container_w.push_back(9);
container_w.push_back(1);
container_w.push_back(8);
container_w.push_back(5);
container_w.push_back(50);
container_w.push_back(6);
loading_backtrack(total_w,container_w);
return 0;
批处理作业调度
问题表述:给定n个作业的集合 J1,J2,…,Jn 。每个作业必须先由机器1处理,然后由机器2处理。作业 Ji 需要机器j的处理时间为 tji 。对于一个确定的作业调度,设 Fji 是作业i在机器j上完成处理的时间。所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。
批处理作业调度问题要求对于给定的n个作业,制定最佳作业调度方案,使其完成时间和达到最小。
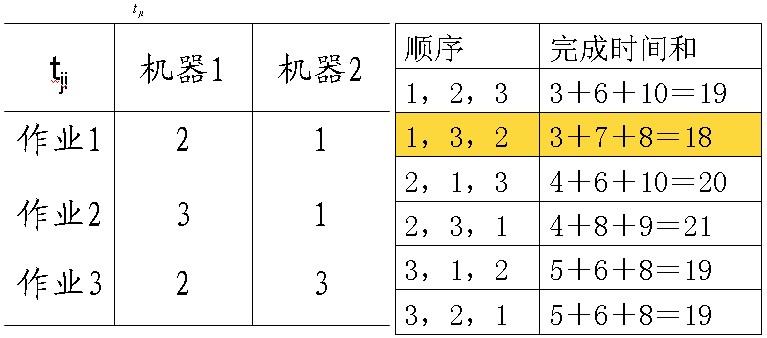
显然,1,3,2是最佳调度方案。
解空间:排列树(将作业顺序进行全排列,分别算出各种情况的完成时间和,取最佳调度方案)

实现:
#include <iostream>
#include <vector>
using namespace std;
class flowshop
public:
flowshop(vector<vector<int> >& rhs)
task_count = rhs.size() ;
each_t = rhs ;
best_t.resize (task_count) ;
machine2_t.resize (task_count,0) ;
machine1_t = 0 ;
total_t = 0 ;
best_total_t = 0 ;
current_t.resize (task_count,0) ;
for (int i = 0 ;i < task_count; ++ i)
current_t[i] = i; // 为了实现全排列
void backtrack ()
__backtrack (0);
// 显示最佳调度方案和最优完成时间和
cout << "the best flowshop scheme is : ";
copy (best_t.begin(),best_t.end(),ostream_iterator<int> (cout, " "));
cout << endl;
cout << "the best total time is : " << best_total_t << endl;
private:
void __backtrack (int i)
if (i >= task_count)
if (total_t < best_total_t || best_total_t == 0)
// 存储当前最优调度方式
copy (current_t.begin(),current_t.end(),best_t.begin()) ;
best_total_t = total_t;
return ;
for (int j = i; j < task_count; ++ j)
// 机器1上结束的时间
machine1_t += each_t[current_t[j]][0] ;
if (i == 0)
machine2_t[i] = machine1_t + each_t[current_t[j]][1] ;
else
// 机器2上结束的时间
machine2_t[i] =
((machine2_t[i - 1] > machine1_t) ? machine2_t[i - 1] : machine1_t)
+ each_t[current_t[j]][1] ;
total_t += machine2_t[i];
// 剪枝
if (total_t < best_total_t || best_total_t == 0)
// 全排列
swap (current_t[i],current_t[j]) ;
__backtrack (i + 1) ;
swap (current_t[i],current_t[j]) ;
machine1_t -= each_t[current_t[j]][0] ;
total_t -= machine2_t[i] ;
public :
int task_count ; // 作业数
vector<vector<int> > each_t ; // 各作业所需的处理时间
vector<int> current_t ; // 当前作业调度
vector<int> best_t ; // 当前最优时间调度