蓝桥杯C/C++程序设计往届真题汇总（进阶篇）

Posted 2023-03-15 比特冬哥

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了蓝桥杯C/C++程序设计往届真题汇总（进阶篇）相关的知识，希望对你有一定的参考价值。

文章目录

1. 最短路

题目描述：
如下图所示，G是一个无向图，其中蓝色边的长度是1、橘色边的长度是2、绿色边的长度是3。

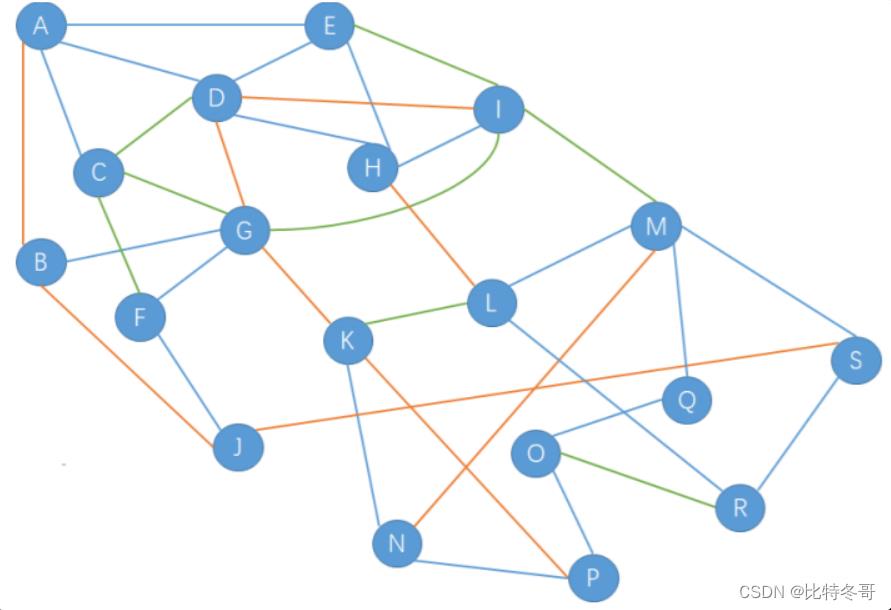
则从 A 到 S 的最短距离是多少？

#include <iostream>
#include <cstring>
using namespace std;
const int N=200,n=19;
int dist[N];
int g[N][N];
void add(char x,char y,int c)

  int a=x-'A'+1;
  int b=y-'A'+1;
  g[a][b]=g[b][a]=c;

bool vis[N];
int dijkstra()

  memset(dist,0x3f,sizeof dist);
  dist[1]=0;
  for(int i=0;i<n;i++)
  
    int t=-1;
    for(int j=1;j<=n;j++)
    
      if(!vis[j]&&(t==-1||dist[j]<dist[t]))
        t=j;
    
    vis[t]=1;

    for(int j=1;j<=n;j++)
    
      dist[j]=min(dist[j],dist[t]+g[t][j]);
    
  
  return dist[n];

int main()

    memset(g,0x3f,sizeof g);
    add('A','B',2);
    add('A','C',1);
    add('A','D',1);
    add('A','D',1);
    add('B','J',2);
    add('B','G',1);
    add('C','D',3);
    add('C','F',3);
    add('C','G',3);
    add('D','E',1);
    add('D','G',2);
    add('D','H',1);
    add('D','I',2);
    add('E','H',1);
    add('E','I',3);
    add('F','G',1);
    add('F','J',1);
    add('G','F',1);
    add('G','I',3);
    add('G','K',2);
    add('H','I',1);
    add('H','L',2);
    add('I','M',3);
    add('J','S',2);
    add('K','N',1);
    add('K','L',3);
    add('K','P',2);
    add('L','M',1);
    add('L','R',1);
    add('M','N',2);
    add('M','Q',1);
    add('M','S',1);
    add('N','P',1);
    add('O','P',1);
    add('O','Q',1);
    add('O','R',3);
    add('R','S',1);
    cout<<dijkstra();
  return 0;

2. 数字三角形

题目描述：

	     7
      3     8
    8    1    0
  2    7    4    4
4   5    2     6    5

上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。
路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个数。此外，向左下走的次数与向右下走的次数相差不能超过1。

【输入描述】
输入的第一行包含一个整数N(1≤N ≤100)，表示三角形的行数。
下面的N行给出数字三角形。数字三角形上的数都是О至100之间的整数。
【输出描述】
输出一个整数，表示答案。

#include<iostream>
using namespace std;
int a[200][200];
int dp[200][200];
int main()

    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    
        for(int j=1;j<=i;j++)
        cin>>a[i][j];
    
    dp[1][1]=a[1][1];
    for(int i=2;i<=n;i++)
    
        for(int j=1;j<=i;j++)
        
            if(j==1)dp[i][j]=dp[i-1][j]+a[i][j];
            else if(j==i)dp[i][j]=dp[i-1][j-1]+a[i][j];
            else dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j];
        
    
    if(n%2==0)
        cout<<max(dp[n][n/2],dp[n][n/2+1]);
    
    else
        cout<<dp[n][n/2+1]<<endl;

3. 递增序列

题目描述：
本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。
对于一个字母矩阵，我们称矩阵中的一个递增序列是指在矩阵中找到两个字母，它们在同一行，同一列，或者在同一45度的斜线上，这两个字母从左向右看、或者从上向下看是递增的。
例如，如下矩阵中

LANN
QIAO

有LN、LN、AN、AN、IO、AO、LQ、AI、NO、NO、等13个递增序列。注意当两个字母是从左下到右上排列时，从左向右看和从上向下看是不同的顺序。
对于下面的30行50列的矩阵，请问总共有多少个递增序列?

VLPWJVVNNZSWFGHSFRBCOIJTPYNEURPIGKQGPSXUGNELGRVZAG
SDLLOVGRTWEYZKKXNKIRWGZWXWRHKXFASATDWZAPZRNHTNNGQF
ZGUGXVQDQAEAHOQEADMWWXFBXECKAVIGPTKTTQFWSWPKRPSMGA
BDGMGYHAOPPRRHKYZCMFZEDELCALTBSWNTAODXYVHQNDASUFRL
YVYWQZUTEPFSFXLTZBMBQETXGXFUEBHGMJKBPNIHMYOELYZIKH
ZYZHSLTCGNANNXTUJGBYKUOJMGOGRDPKEUGVHNZJZHDUNRERBU
XFPTZKTPVQPJEMBHNTUBSMIYEGXNWQSBZMHMDRZZMJPZQTCWLR
ZNXOKBITTPSHEXWHZXFLWEMPZTBVNKNYSHCIQRIKQHFRAYWOPG
MHJKFYYBQSDPOVJICWWGGCOZSBGLSOXOFDAADZYEOBKDDTMQPA
VIDPIGELBYMEVQLASLQRUKMXSEWGHRSFVXOMHSJWWXHIBCGVIF
GWRFRFLHAMYWYZOIQODBIHHRIIMWJWJGYPFAHZZWJKRGOISUJC
EKQKKPNEYCBWOQHTYFHHQZRLFNDOVXTWASSQWXKBIVTKTUIASK
PEKNJFIVBKOZUEPPHIWLUBFUDWPIDRJKAZVJKPBRHCRMGNMFWW
CGZAXHXPDELTACGUWBXWNNZNDQYYCIQRJCULIEBQBLLMJEUSZP
RWHHQMBIJWTQPUFNAESPZHAQARNIDUCRYQAZMNVRVZUJOZUDGS
PFGAYBDEECHUXFUZIKAXYDFWJNSAOPJYWUIEJSCORRBVQHCHMR
JNVIPVEMQSHCCAXMWEFSYIGFPIXNIDXOTXTNBCHSHUZGKXFECL
YZBAIIOTWLREPZISBGJLQDALKZUKEQMKLDIPXJEPENEIPWFDLP
HBQKWJFLSEXVILKYPNSWUZLDCRTAYUUPEITQJEITZRQMMAQNLN
DQDJGOWMBFKAIGWEAJOISPFPLULIWVVALLIIHBGEZLGRHRCKGF
LXYPCVPNUKSWCCGXEYTEBAWRLWDWNHHNNNWQNIIBUCGUJYMRYW
CZDKISKUSBPFHVGSAVJBDMNPSDKFRXVVPLVAQUGVUJEXSZFGFQ
IYIJGISUANRAXTGQLAVFMQTICKQAHLEBGHAVOVVPEXIMLFWIYI
ZIIFSOPCMAWCBPKWZBUQPQLGSNIBFADUUJJHPAIUVVNWNWKDZB
HGTEEIISFGIUEUOWXVTPJDVACYQYFQUCXOXOSSMXLZDQESHXKP
FEBZHJAGIFGXSMRDKGONGELOALLSYDVILRWAPXXBPOOSWZNEAS
VJGMAOFLGYIFLJTEKDNIWHJAABCASFMAKIENSYIZZSLRSUIPCJ
BMQGMPDRCPGWKTPLOTAINXZAAJWCPUJHPOUYWNWHZAKCDMZDSR
RRARTVHZYYCEDXJQNQAINQVDJCZCZLCQWQQIKUYMYMOVMNCBVY
ABTCRRUXVGYLZILFLOFYVWFFBZNFWDZOADRDCLIRFKBFBHMAXX

#include <iostream>
using namespace std;
int main()

    char str[35][55];
    long int ans = 0;
    for(int i=0; i<30; i++)
        for(int j=0; j<50; j++)
        
          cin >> str[i][j];
        
    
    for(int i=0; i<30; i++)
        for(int j=0; j<50; j++)
        
            int k;
            for(k=1; k+j<50; k++)//列 
            
                if(str[i][j] < str[i][j+k])
                    ans++;
                
            
            for(k=1; k+i<30; k++)//行 
            
                if(str[i][j] < str[i+k][j])
                    ans++;
                
            
            for(k=1; k+i<30 && j+k<50; k++) //从左上到右下
            
                if(str[i+k][j+k] > str[i][j])
                    ans++;    
             
        
    
    for(int i=1; i<30; i++)
        for(int j=0; j<50; j++)
        
            int k;
            for(k=1; i-k>=0 && j+k<50; k++)//左下到右上 
            
                if(str[i][j] != str[i-k][j+k]) 
                    ans++;
            
        
    
        
    cout << ans << endl;
    return 0;

4. 杨辉三角形

题目描述：

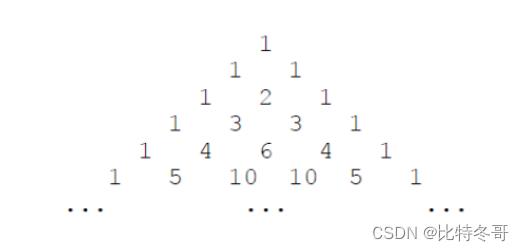
如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列: 1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,…
给定一个正整数N，请你输出数列中第一次出现N是在第几个数?

【输入描述】
输入一个整数N。
【输出描述】
输出一个整数代表答案。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n;
/*   1
   1 2 1
  1 3 3 1
 1 4 6 4 1
1 5 10 10 5 1
可以发现找到第一个出现的一定在左边故右边可以直接删去
           1
         1 2
       1 3
     1 4 6
   1 5 10
 1 6 15 20
/ / / /
从打斜杠的地方可以发现规律为C(2n,n)
故找到最大的斜行
用t来代表斜行数
最大为1e9；
故求有多少个斜行数满足？
int x;//记录第几个斜行满足
for(int t=0;;t++)
if(1e9<=C(2t,t))
 x=t;
 break;


故解得t=17;
斜线从大到小依次排列第一找到第一个数
再通过二分查找
C(t, k)对应的顺序值为：(t + 1) * t / 2 + k + 1
*/
LL C(int x,int k)
  LL ans=1;
  for(int i=x,j=1;j<=k;i--,j++)
    ans=ans*i/j;
    if(ans>n)return ans;
  
  return ans;

bool check(int x)
  LL l=2*x,r=max(n,l);
  while(l<r)
    int mid=l+r>>1;
    if(C(mid,x)>=n)r=mid;
    else l=mid+1;
  
  if(C(r,x)!=n)return false;
  cout<<(LL)(r+1)*r/2+x+1<<endl;
  return true;

int main()
  cin>>n;
  for(int t=17;;t--)
    if(check(t))break;
  
  return 0;

5. 跳跃

题目描述：
小蓝在一个n行m列的方格图中玩一个游戏。
开始时，小蓝站在方格图的左上角，即第1行第1列。
小蓝可以在方格图上走动，走动时，如果当前在第r行第c列，他不能走到行号比r小的行，也不能走到列号比c 小的列。同时，他一步走的直线距离不超过3。
例如，如果当前小蓝在第3行第5列，他下一步可以走到第3行第6列、第3行第7列、第3行第8列、第4行第5列、第4行第6列、第4行第7列、第5行第5列、第5行第6列、第6行第5列之一。
小蓝最终要走到第n行第m列。
在图中，有的位置有奖励，走上去即可获得，有的位置有惩罚，走上去就要接受惩罚。奖励和惩罚最终抽象成一个权值，奖励为正，惩罚为负。
小蓝希望，从第1行第1列走到第n行第m列后，总的权值和最大。请问最大是多少?

【输入描述】
输入的第一行包含两个整数n, m，表示图的大小。
接下来n行，每行m个整数，表示方格图中每个点的权值。其中，1≤n ≤100，-10⁴≤权值≤10⁴。
【输出描述】
输出一个整数，表示最大权值和。

//宽度搜索
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 110;
int n, m;
int map[N][N];
int res = -1e9;
int px[9] =  0,0,0,1,2,3,1,1,2 , py[9] =  1,2,3,0,0,0,1,2,1 ;

void bfs(int x, int y, int sum) 
    if (x == n && y == m) 
        res = max(sum, res);
    
    else 
        for (int i = 0; i < 9; i++) 
            int px1 = x + px[i];
            int py1 = y + py[i];
            if (px1 <= n && py1 <= m) 
                int sum1 = map[px1][py1] + sum;
                bfs(px1, py1, sum1);
            
        
    


int main() 
    cin >> n >> m;
    for (int i = 1; i <= n; i++) 
        for (int j = 1; j <= m; j++) 
            cin >> map[i][j];
        
    
    bfs(1, 1, map[1][1]);
    cout << res << endl;

6. 路径

题目描述：
小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图中的最短路径。
小蓝的图由2021个结点组成，依次编号1至2021。
对于两个不同的结点a, b，如果a和b的差的绝对值大于21，则两个结点之间没有边相连;如果a和b的差的绝对值小于等于21，则两个点之间有一条长度为a和 b的最小公倍数的无向边相连。
例如:结点1和结点23之间没有边相连;结点3和结点24之间有一条无向边，长度为24;结点15和结点25之间有一条无向边，长度为75。
请计算，结点1和结点2021之间的最短路径长度是多少。

蓝桥杯第六届C/C++ B组真题详解
 第十二届蓝桥杯省赛第一场C/C++ B组真题及部分题解
 蓝桥杯C语言题目
 蓝桥杯真题2021年蓝桥杯省赛A组题目解析+代码（python组）
 2018年第九届 蓝桥杯C组 C/C++决赛题解
 # 2020年第十一届蓝桥杯C/C++ B组第二场省赛真题

蓝桥杯C/C++程序设计 往届真题汇总（进阶篇）