数学高中三角函数的温习
Posted 花姓-老花
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学高中三角函数的温习相关的知识,希望对你有一定的参考价值。
就个人在开发中的总结,发现数学这东西越使越好使,所以就决定回顾一下相关数学知。这一篇主要针对是三角函数知识点,供自己往后开发时查阅带来便利
三角形基本知识
三角形按角度分类:锐角、直角和钝角三角形
三角形按边长分类:不等边三角形和等边三角形【底边和腰不相等的等腰三角形和等边三角形】
三角形具有稳定性,而四边形没有稳定性
三角形的内角、外角和三边关系
⑴三角形的内角和等于180°,三角的外角和等于360°
⑵三角形的外角性质
①三角形的一个外角等于与它不相邻的两个内角的和
②三角形的一个外角大于任何一个与它不相邻的内角
⑶三角形的三边关系
三角形任意两边之和大于第三边,任意两边之差小于第三边
三角形的高线、中线、角平分线
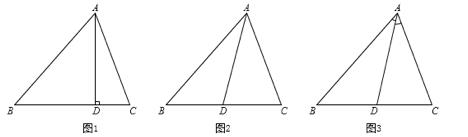
⑴从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段称作三角形的高(图1)
⑵在三角形中,连接一个顶点和它的对边的中点的线段叫做三角形的中线(图2)
⑶三角形中一个角的平分线与这个角对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线(图3)
三角形中位线
定义:连接三角形两边中点的线段叫做三角形的中位线
三角形中位线定理:三角形中位线平行于第三边,且等于第三边的一半
三角函数
说到三角函数都是要结合坐标来进行分析
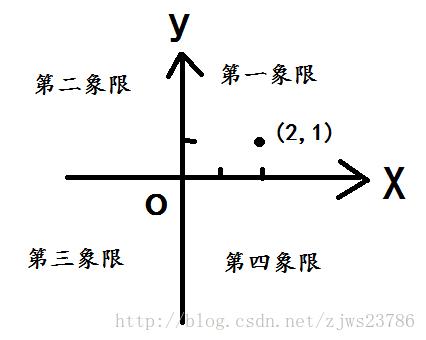
坐标和象限关系
度和弧度关系
度定义:两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆周长的360分之一时,两条射线的夹角的大小为1度(图一)
弧度定义:两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长等于圆的半径时,两条射线的夹角大小为1弧度(图二)

一周的弧度数为2πr/r=2π
∵2πr/r=2π
∴ 360°角=2π
1弧度约为57.3°,即57°17′44.806″。1°为π/180弧度,近似值为0.01745弧度,周角为2π弧度,平角(即180°角)为π弧度,直角为π/2弧度
弧长公式:
弧长=nπr/180【n就是角度数,即圆心角n所对应的弧长 注:弧度有正负之分】
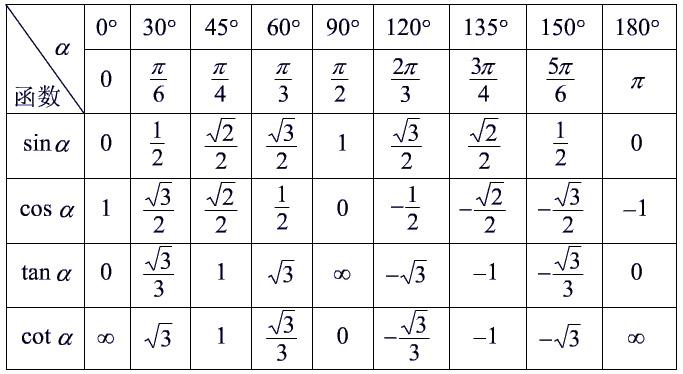
| 度 | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| 弧度 | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 3π/2 | 2π |
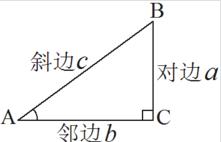
正弦函数定义:在Rt△ABC(直角三角形)中,∠C=90º,任意一锐角∠A的对边与斜边的比叫做∠A的正弦,即sinA = a/c
余弦函数定义:在Rt△ABC(直角三角形)中,∠C=90º,∠A的余弦是它的邻边比三角形的斜边,即cosA=b/c
正切函数定义:在Rt△ABC(直角三角形)中,∠C=90º,∠A的正切是它的对边与邻边比叫做∠A的正切,即tanA=a/b
三角函数公式

函数关系
倒数关系:①tanα cotα=1 ②sinα cscα=1 ③cosα secα=1
商数关系:①tanα=sinα/cosα ②cotα=cosα/sinα
平方关系:①sin²α+cos²α=1 ②1+tan²α=sec²α ③1+cot²α=csc²α
三角形定理
正弦定理是三角学中一个基本定理,它指出“在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆半径的2倍”,即a/sinA = b/sinB=c/sinC=2r=D(r为外接圆半径,D为直径)
在任意△ABC中,角A、B、C所对的边长分别为a、b、c,三角形外接圆的半径为R,则有:
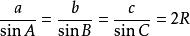
正弦定理变形得:
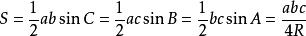
a∶b∶c=sinA∶sinB∶sinC
公式含义:对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积,若三边为a、b、c三角为A(α),B(β),C(γ),如图所示:
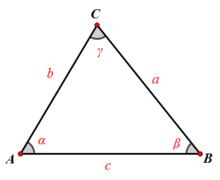
c²=a²+b²-2ab cos(γ) 或 b²=c²+a²-2ac cos(β) 或 a²=b²+c²-2bc cos(α)
勾股定理是余弦定理的特例,当γ为90º时,cos(γ)=0,余弦定理可简化为c²=a²+b²
公式变换
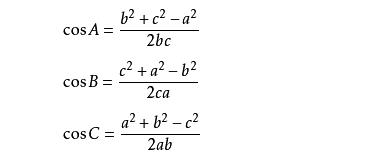
平面几何证明
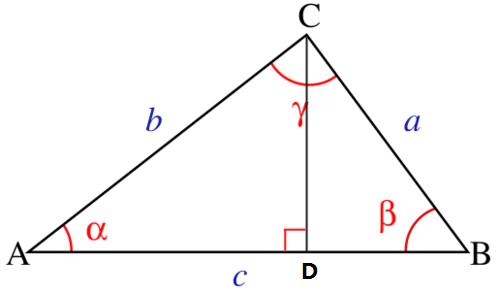
如上图所示,△ABC,在c上做高,将c边写成:
c=a cos(β)+b cos(α)
证明:
∵AD+BD=c cosα=AD/b cosβ=BD/a
∴ AD=b cosα BD=a cosβ a cosβ+b cosβ =AD+BD=c
根据上面可以引导出下面用法

余弦函数应用
①当已知三角形的两边及其夹角,可由余弦定理得出已知角的对边
②当已知三角形的三边,可以由余弦定理得到三角形的三个角
③当已知三角形的三边,可以由余弦定理得到三角形的面积
求面积(上图三角形面积)
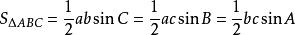
如果已知三角形的三条边,可以有余弦定理求出内角,从而得到三角形的面积。
三角函数诱导公式
两角和差公式
两角和差公式
sin(α+β)=sinαcosβ+cosαsinβ sin(α-β)=sinαcosβ-cosαsinβ cos(α+β)=cosαcosβ-sinαsinβ cos(α-β)=cosαcosβ+sinαsinβ tan(α+β)=(tanα+tanβ )/(1-tanαtanβ) tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)二倍角的正弦、余弦和切公式
sin 2(α/2)=(1-cosα)/2 cos 2(α/2)=(1+cosα)/2 tan 2(α/2)=(1-cosα)/(1+cosα) tan(α/2)=(1—cosα)/sinα=sinα/1+cosα
特殊值表
函数图像
| 函数 | 对称轴 | 对称中心 | 图象 |
|---|---|---|---|
| y=sin x 正弦函数 | x=kπ+π/2(k∈Z) | (kπ,0)(k∈Z) |
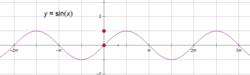 正弦函数
正弦函数
|
| y=cos x 余弦函数 | x=kπ(k∈Z) | (kπ+π/2,0)(k∈Z) |
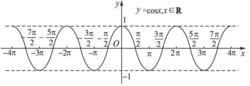 余弦函数
余弦函数
|
| y=tan x 正切函数 | 无 | (kπ/2+π/2,0)(k∈Z) |
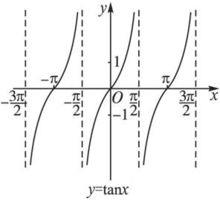 正切函数
正切函数
|
| y=cot x 余切函数 | 无 | (kπ/2,0)(k∈Z) |
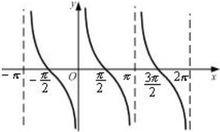 余切函数
余切函数
|
| y=sec x 正割函数 | x=kπ(k∈Z) | (kπ+π/2,0)(k∈Z) | 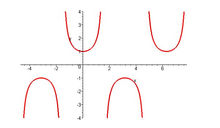 |
| y=csc x 余割函数 | x=kπ+π/2(k∈Z) | (kπ,0)(k∈Z) | 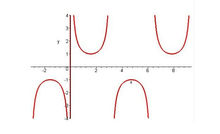 |
以上是关于数学高中三角函数的温习的主要内容,如果未能解决你的问题,请参考以下文章