叠加性（Additivity）什么情况下可以导出齐次性(Homogeneity)?

Posted 2023-03-09 卓晴

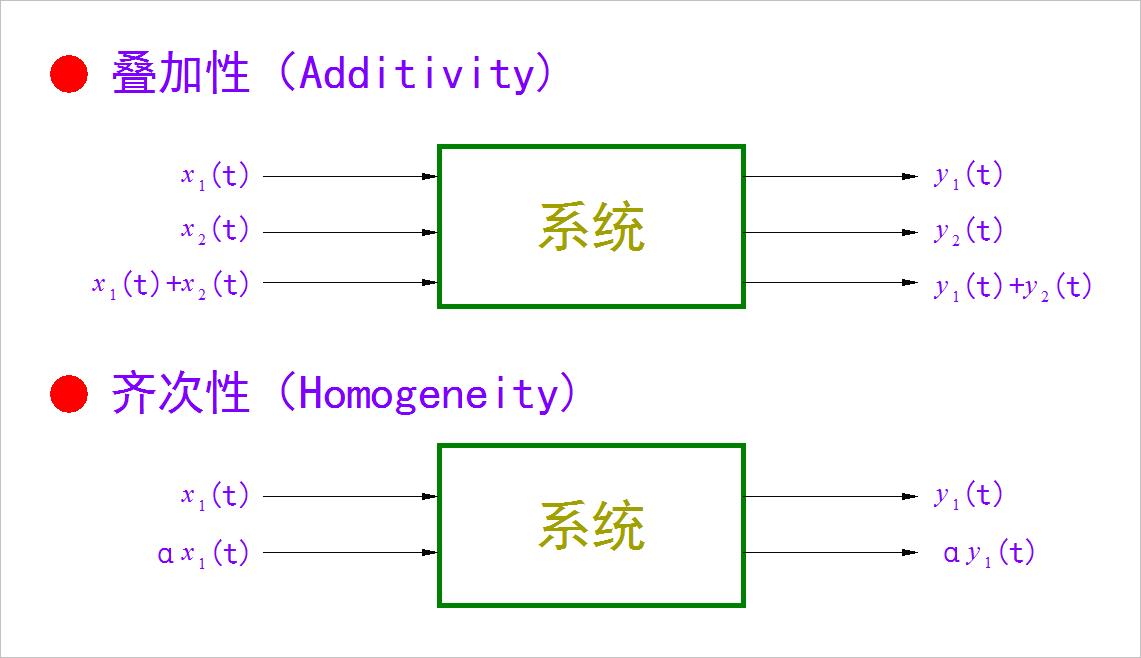
系统的线性特性

 

01 线性系统

---

一、背景介绍

  今天在信号与系统课程中，讲解线性系统需要同时满足两个特性： 一是叠加性。 当两个输入信号x1,x2分别引起输出y1,y2。 那么x1+x2所引起的系统输出等于y1+y2。 第二个特性是齐次性， 输入信号x1引起系统的输出为 y1。 对应 a 倍的 x1 引起系统输出是 a 倍的y1。 这两个特性需要分别进行验证。

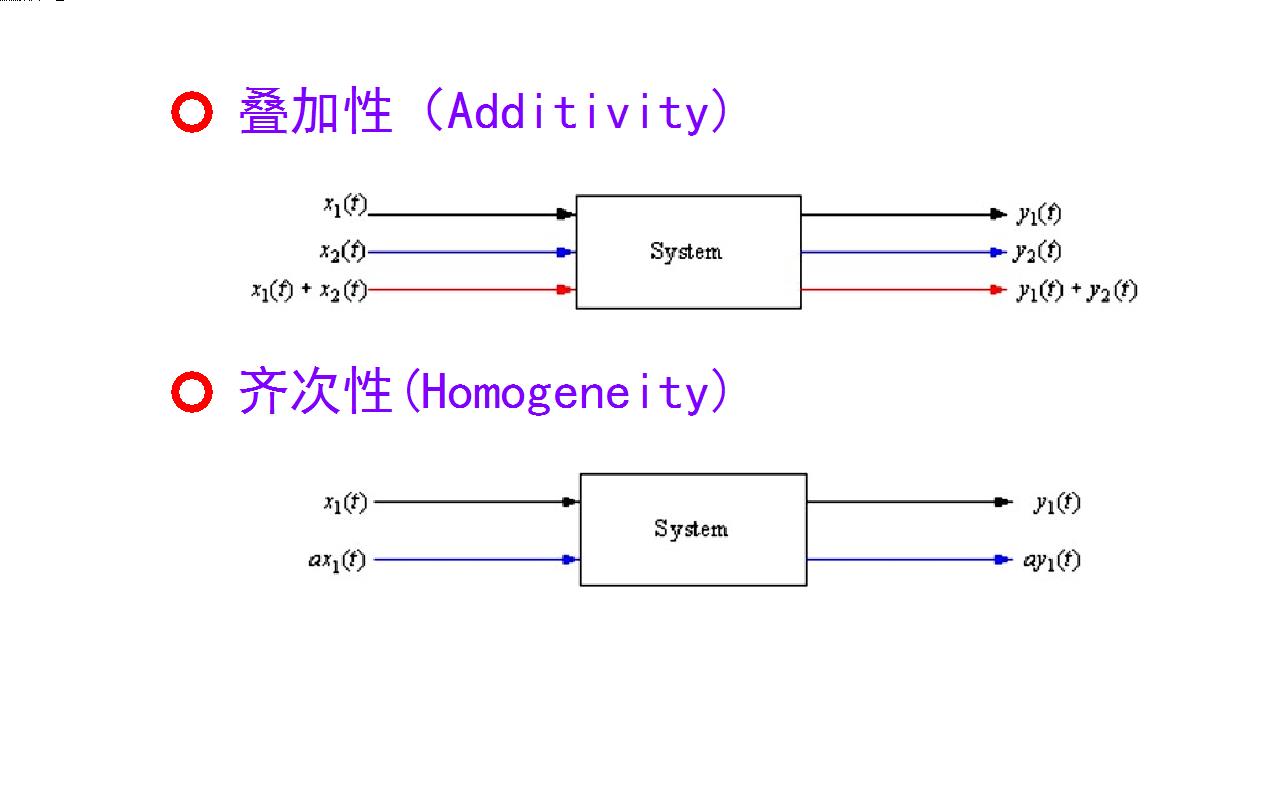
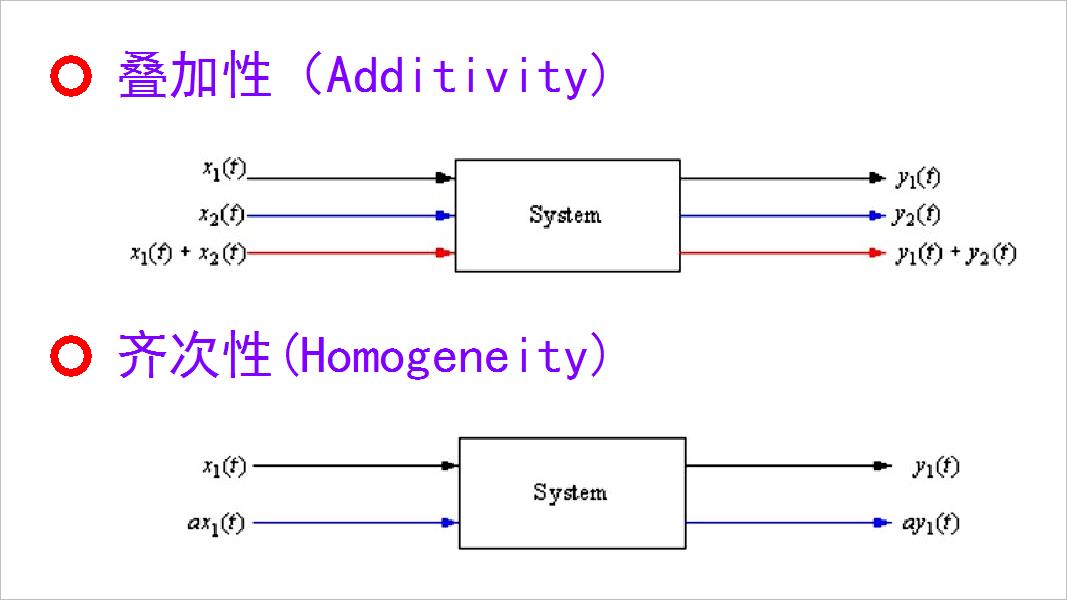
▲ 图1.1.1 线性系统两个特性

二、相关举例

  关于系统的线性两个条件， 在数学中的函数、映射中也有相应的讨论。 叠加性和齐次性是相互独立的两个性质。 通常情况下， 举例说明满足其次关系的系统，不能满足叠加性相对比较容易。 但是举例说明满足叠加性的系统，不能满足齐次性相对困难。 这主要是常见到的工程应用中碰到的系统大体都是实数信号，而且满足连续性。 在这种情况下，满足叠加性的系统往往就能够满足齐次性。

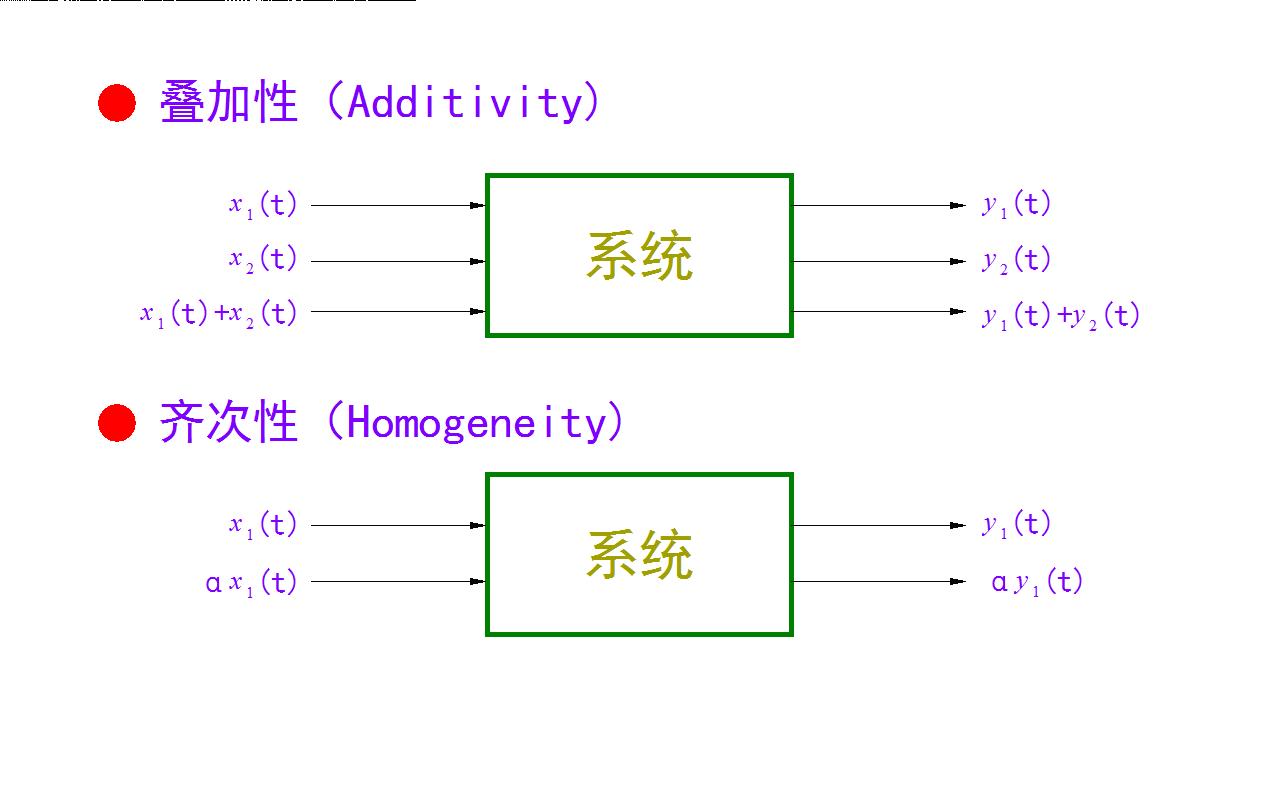
  根据维基百科中关于数学中线性的定义， 对于限定尺度数字 a 为有理数时， 叠加性意味着线性，并给出了简要的证明。 对于连续函数， 可以将比例系数 a 放宽到实数范围。 这是根据有理数在实数范围内具有稠密特性来决定的。

• One short-of-linear functon: Does f(x+y)=f(x)+f(y) imply f(ax)=af(x)?
• Additivity and Homogeneity
• Additive but not homogeneous continuous system?
• Wikipedia article on linear system

▲ 图1.1.2 One Example

  在这篇“课堂胶囊”网文中， 作者总结本科数学教学经验，给出了叠加性 与齐次性的讨论。 并给出了一些反例。 如果齐次性的比例系数放宽到复数， 作者给出了一个最常见到的映射关系。 比如 T7，取输入信号的实部， 它满足叠加性。如果尺度数字是复数的情况下， 这个映射不满足其次特性。

  在这篇博文中对满足叠加性是否预示着齐次性进行了讨论。 作者构造了一个实数域内的一个映射，满足叠加性但不满足齐次性。  下面我们看一下这个例子。

  定义在有理数向量空间的一个映射 Q。 对于每一有理数对（a,b），它们对应的一个实数 a 加上 b 倍的 根号 2。 经过映射后等于有理数 a+b。 很容易验证这个映射在向量空间 Q 中 满足叠加性。 构造比例因子alpha， 可以验证在 alpha 尺度下， 这个映射不满足齐次性。 对于这个反例， 作者也认为存在一定缺陷， 比如这个比例因子不属于原来向量空间 Q， 而是属于向量空间 Q，根号2。 这个例子也说明，构建实数域内的反例不是太容易。

 

※ 总  结 ※

---

  本文讨论了信号与系统中的线性概念。 在数学概念中，线性系统需要同时满足叠加性和齐次性。 但在实际常见到的连续时间系统中， 都是实数信号，且都满足连续性。 所以只要满足叠加性就可以了。

---

■ 相关文献链接:

• One short-of-linear functon: Does f(x+y)=f(x)+f(y) imply f(ax)=af(x)?
• Additivity and Homogeneity
• Additive but not homogeneous continuous system?
• Wikipedia article on linear system

● 相关图表链接:

• 图1.1.1 线性系统两个特性
• 图1.1.2 One Example