D. Happy Tree Party CodeForces 593D树链剖分，树边权转点权

Posted 2021-03-25 茄子Min

Codeforces Round #329 (Div. 2)

D. Happy Tree Party

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Bogdan has a birthday today and mom gave him a tree consisting of n vertecies. For every edge of the tree i, some number *x**i* was written on it. In case you forget, a tree is a connected non-directed graph without cycles. After the present was granted, m guests consecutively come to Bogdan‘s party. When the i-th guest comes, he performs exactly one of the two possible operations:

1. Chooses some number yi, and two vertecies ai and bi. After that, he moves along the edges of the tree from vertex ai to vertex *b**i* using the shortest path (of course, such a path is unique in the tree). Every time he moves along some edge j, he replaces his current number *y**i* by 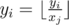, that is, by the result of integer division *y**i* div *x**j*.
2. Chooses some edge *p**i* and replaces the value written in it xpi by some positive integer *ci?<?xp**i*.

As Bogdan cares about his guests, he decided to ease the process. Write a program that performs all the operations requested by guests and outputs the resulting value *y**i* for each i of the first type.

Input

The first line of the input contains integers, n and m (2?≤?n?≤?200?000, 1?≤?m?≤?200?000) — the number of vertecies in the tree granted to Bogdan by his mom and the number of guests that came to the party respectively.

Next n?-?1 lines contain the description of the edges. The i-th of these lines contains three integers ui, vi and *x**i* (1?≤?ui,?vi?≤?n, ui?≠?vi, 1?≤?xi?≤?1018), denoting an edge that connects vertecies ui and vi, with the number xi initially written on it.

The following m lines describe operations, requested by Bogdan‘s guests. Each description contains three or four integers and has one of the two possible forms:

• 1 *a**i* *b**i* *y**i* corresponds to a guest, who chooses the operation of the first type.
• 2 *p**i* *c**i* corresponds to a guests, who chooses the operation of the second type.

It is guaranteed that all the queries are correct, namely ,1?≤?pi?≤?n?-?1 , wherexpirepresents a number written on edgepiat this particular moment of time that is not necessarily equal to the initial valuexpi

Output

For each guest who chooses the operation of the first type, print the result of processing the value *y**i* through the path from *a**i* to *b**i*.

Examples

input

Copy

6 61 2 11 3 71 4 42 5 52 6 21 4 6 172 3 21 4 6 171 5 5 202 4 11 5 1 3

output

Copy

24203

input

Copy

5 41 2 71 3 33 4 23 5 51 4 2 1001 5 4 12 2 21 1 3 4

output

Copy

202

Note

Initially the tree looks like this:

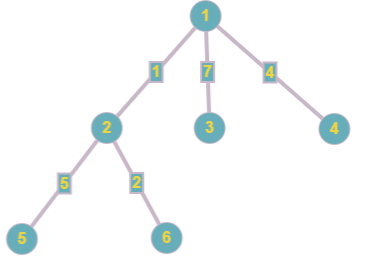
The response to the first query is: 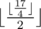= 2

After the third edge is changed, the tree looks like this:

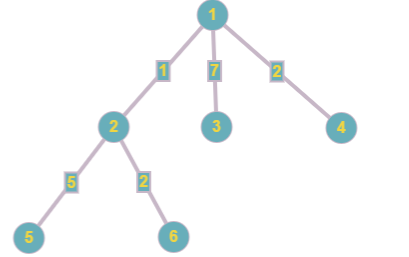
The response to the second query is: 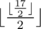= 4

In the third query the initial and final vertex coincide, that is, the answer will be the initial number 20.

After the change in the fourth edge the tree looks like this:

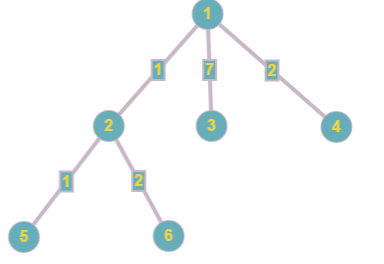
In the last query the answer will be: 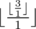= 3

题意：

可以去这个链接阅读中文题意：

https://vjudge.net/problem/CodeForces-593D#author=AwayWithCorrect

思路：

• 1：边权转为点权建树：

  确定一个root后，在dfs过程中，把边权值放在深度较大的节点的点权上。

  这样建树的话，询问路径(x->y)的时候的边权sum和，实际求的过程中，点权只需要计算从（x到y路径的中的下一个节点z）到y节点的点权sum和。因为x的点权是root到x中的x上方的边权，并不在x到y的路径中。

• 2：树链剖分，同时用线段树维护连续点权的累乘积。

• 3：当线段树中的一个线段权值>1e18后，给该线段加个标记，或者权值定为0，因为询问是<=1e18的，那么如果询问包括了这个权值，答案一定是0.

• 4：更新边的权值时，直接用线段树更新那条边中深度更大的点权即可。

• 5：在树链剖分询问路径的过程中，别忘记1中讲到了去掉x节点点权，可以直接在最后的一个query中把id[x]（x的dfs序）改为id[x]+1,因为一条链中dfs序时连续的。

判定x*y是否会超过1e18可以用这个函数的写法来求：

long long mul(long long aaa,long long bbb)
{
    if(aaa==0||bbb==0)
        return 0;
    if(INF/aaa<bbb)
    {
        return 0;
    }
    else
        return aaa*bbb;
}

## AC代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {ll ans = 1; while (b) {if (b % 2)ans = ans * a % MOD; a = a * a % MOD; b /= 2;} return ans;}
inline void getInt(int* p);
const int maxn = 600010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
int n, m;
int root;
ll a[maxn];// 初始点权
ll wt[maxn];// 新建编号点权。
int cnt;// 编号用的变量
int top[maxn];// 所在重链的顶点编号
int id[maxn];//节点的新编号。
typedef pair<int, ll> pil;
std::vector<pil> son[maxn];
int SZ[maxn];// 子数大小
int wson[maxn];// 重儿子
int fa[maxn];// 父节点
int dep[maxn];// 节点的深度

void dfs1(int id, int pre, int step) // 维护出sz,wson,fa,dep
{
    dep[id] = step;
    fa[id] = pre;
    SZ[id] = 1;
    int  maxson = -1;
    for (auto x : son[id])
    {
        if (x.fi != pre)
        {
            a[x.fi] = x.se;
            dfs1(x.fi, id, step + 1);
            SZ[id] += SZ[x.fi];
            if (SZ[x.fi] > maxson)
            {
                maxson = SZ[x.fi];
                wson[id] = x.fi;
            }
        }
    }

}

//处理出top[],wt[],id[]
void dfs2(int u, int topf)
{
    id[u] = ++cnt;
    wt[cnt] = a[u];
    top[u] = topf;
    if (!wson[u]) // 没儿子时直接结束
    {
        return ;
    }
    dfs2(wson[u], topf); // 先处理重儿子
    for (auto x : son[u])
    {
        if (x.fi == wson[u] || x.fi == fa[u]) //只处理轻儿子
        {
            continue;
        }
        dfs2(x.fi, x.fi); // 每个轻儿子以自己为top
    }
}

struct node
{
    int l, r;
    ll sum;
} segment_tree[maxn << 2];

int getwei(ll x)
{
    int res = 0;
    while (x)
    {
        res++;
        x /= 10;
    }
    return res;
}
ll num_1e18 = 1e18;
ll getcheng(ll v1, ll v2)
{
    if (v1 == 0ll || v2 == 0ll)
    {
        return 0ll;
    }
    int x1 = getwei(v1);
    int x2 = getwei(v2);
    ll res;
    if (x1 + x2 > 20)
    {
        res = 0ll;
    } else if (x1 + x2 == 20 && num_1e18 / v2 == v2)
    {
        res = 0ll;
    } else
    {
        res = (v1 * v2);
    }
    return res;
}
void pushup(int rt)
{
    segment_tree[rt].sum = getcheng(segment_tree[rt << 1].sum, segment_tree[rt << 1 | 1].sum);
}
void build(int rt, int l, int r)
{
    segment_tree[rt].l = l;
    segment_tree[rt].r = r;
    if (l == r)
    {
        segment_tree[rt].sum = wt[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);
    build(rt << 1 | 1, mid + 1, r);
    pushup(rt);
}

void update(int rt, int pos, ll val)
{
    if (segment_tree[rt].l == pos && segment_tree[rt].r == pos)
    {
        segment_tree[rt].sum = min(segment_tree[rt].sum, val);
        return ;
    }
    int mid = (segment_tree[rt].l + segment_tree[rt].r) >> 1;
    if (mid >= pos)
    {
        update(rt << 1, pos, val);
    }
    if (mid < pos)
    {
        update(rt << 1 | 1, pos, val);
    }
    pushup(rt);
}

ll query(int rt, int l, int r)
{
    if (l > r)
    {
        return 1ll;
    }
    if (segment_tree[rt].l >= l && segment_tree[rt].r <= r)
    {
        return segment_tree[rt].sum;
    }
    int mid = (segment_tree[rt].l + segment_tree[rt].r) >> 1;
    ll res = 1ll;
    if (mid >= l)
    {
        res = getcheng(res, query(rt << 1, l, r));
    }
    if (mid < r)
    {
        res = getcheng(res, query(rt << 1 | 1, l, r));
    }
    return res;

}


void uprange(int x, int y, ll k)
{

    if (dep[x] < dep[y]) // 使x的top深度较大
    {
        swap(x, y);
    }
    update(1, id[x], k);
}

ll qrange(int x, int y)
{
    ll ans = 1ll;
    while (top[x] != top[y])
    {
        if (dep[top[x]] < dep[top[y]])
        {
            swap(x, y);
        }
        ans = getcheng(ans, query(1, id[top[x]], id[x]));
        x = fa[top[x]];
    }
    if (dep[x] > dep[y])
        swap(x, y);
    ans = getcheng(ans, query(1, id[x] + 1, id[y]));
    return ans;
}
pii info[maxn];
int main()
{
//    freopen("D:common_textcode_streamin.txt","r",stdin);
//    freopen("D:common_textcode_streamout.txt","w",stdout);

    gbtb;
//    chu(getwei(1e9));
    cin >> n >> m;
    root = 1;
    int u, v;
    ll val;
    repd(i, 1, n - 1)
    {
        cin >> u >> v >> val;
        son[u].pb(mp(v, val));
        son[v].pb(mp(u, val));
        info[i] = mp(u, v);
    }
    dfs1(root, 0, 1);
    dfs2(root, root);
    build(1, 1, n);
    int op, x, y;
    ll z;
    int isok = 0;
    if (info[1].fi == 7610 && info[1].se == 132654)
    {
        isok = 1;
    }
    while (m--)
    {
        cin >> op;
        if (op == 1)
        {
            cin >> x >> y >> z;
            val = qrange(x, y);
            // if (isok)
            // {
            //     cout << " 1: " << val << endl;
            // }
            if (val == 0)
            {
                cout << val << endl;
            } else
            {
                cout << z / val << endl;
            }
        } else if (op == 2)
        {
            cin >> x >> z;
            uprange(info[x].fi, info[x].se, z);
        }
    }

    return 0;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '
');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    }
    else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}


?