deep_thoughts36_爱因斯坦标示法与PyTorch联合

Posted 2023-03-09 研1菜鸟

视频链接：https://www.bilibili.com/video/BV1ZY411b78A/?spm_id_from=333.999.0.0

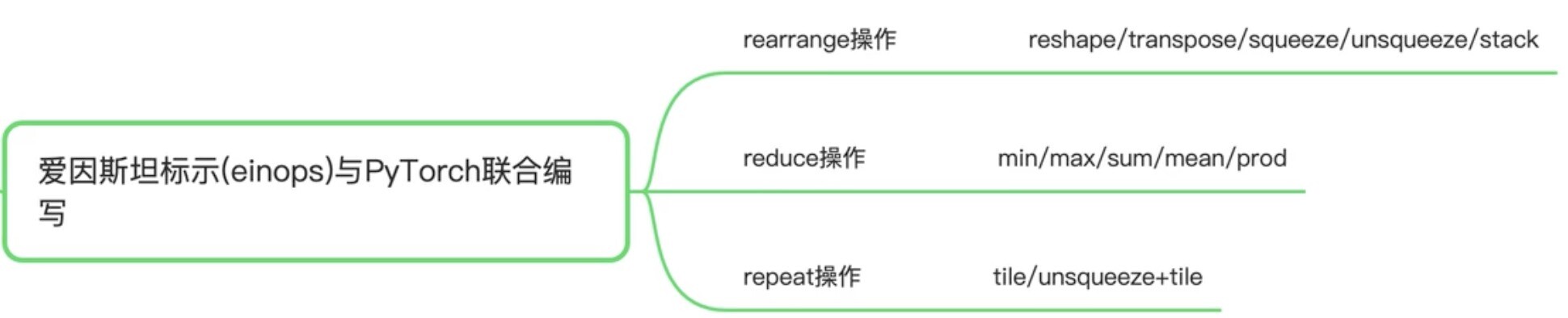
代码：

import torch
from einops import rearrange, reduce, repeat

x = torch.randn(2, 3, 4, 5)  # 4D tensor: bs*ic*h*w


# 1.转置
# 例：交换第1、2维
out1 = x.transpose(1, 2)
out2 = rearrange(x, 'b i h w -> b h i w')  # 字母任意，也可以是abcd->acbd
flag = torch.allclose(out1, out2)  # 验证两个tensor是否按元素相等
print(flag)  # True

# 2.变形
out1 = x.view(-1, x.shape[-2], x.shape[-1])  # x.reshape(6, 4, 5)
out2 = rearrange(x, 'b i h w -> (b i) h w')  # 例：将前两维合并成1个维度，四维变三维
out3 = rearrange(out2, '(b i) h w -> b i h w', b=2)  # 三维变四维,指定b=2，不然不知道是1*6或2*3或3*2或6*1
flag = torch.allclose(out1, out2)
print(flag)  # True
flag = torch.allclose(x, out3)
print(flag)  # True

# 3.image2patch
x = torch.randn(2, 3, 6, 6)
out1 = rearrange(x, 'b i (h1 p1) (w1 p2) -> b (h1 w1) (p1 p2 i)', p1=3, p2=3)  # p1,p2是patch的高度和宽度，不能统一成p，会报错
# 下面两句与上面一句相同
out1 = rearrange(x, 'b i (h1 p1) (w1 p2) -> b i (h1 w1) (p1 p2)', p1=3, p2=3)  # [2,3,4,9]
out2 = rearrange(out1, 'b i n a -> b n (i a)')  # [2,4,27]
print(out2.shape)  # [batch_size, num_patches, patch_depth]


# 4.求平均池化等
out1 = reduce(x, 'b i h w -> b i h', reduction='mean')  # 对最后一维进行平均池化
out2 = reduce(x, 'b i h w -> b i h 1', 'sum')  # 对最后一维求和，并保持维度不变
out3 = reduce(x, 'b i h w -> b i', 'max')  # 对 h 和 w 维进行最大池化
print(out1.shape)  # [2,3,6]
print(out2.shape)  # [2,3,6,1]
print(out3.shape)  # [2,3]

# 5.堆叠张量
tensor_list = [x, x, x]
out1 = rearrange(tensor_list, 'n b i h w -> n b i h w')
print(out1.shape)  # torch.Size([3, 2, 3, 6, 6]) 列表在第0维堆叠成张量

# 6.扩维
out1 = rearrange(x, 'b i h w -> b i h w 1')  # 类似于 torch.unsqueeze
print(out1.shape)  # [2, 3, 6, 6, 1]

# 7.复制
out2 = repeat(out1, 'b i h w 1 -> b i h w 2')  # 类似于 torch.tile
print(out2.shape)  # [2, 3, 6, 6, 2]

out3 = repeat(x, 'b i h w -> b i (2 h) (2 w)')
print(out3.shape)  # [2, 3, 12, 12]

注意：有的是用repeat，有的是rearrange，有的是reduce，注意分辨。