基于参数化最小互熵(Parametric Minimum Cross Entropy,PMCE)算法的PAPR抑制matlab仿真
Posted fpga和matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于参数化最小互熵(Parametric Minimum Cross Entropy,PMCE)算法的PAPR抑制matlab仿真相关的知识,希望对你有一定的参考价值。
目录
一、理论基础
在通信系统中,信道所能提供的带宽通常比传送一路信号所需的带宽要宽得多。如果一个信道只传送一路信号是非常浪费的,为了能够充分利用信道的带宽,就可以采用频分复用的方法。
OFDM主要思想是:将信道分成若干正交子信道,将高速数据信号转换成并行的低速子数据流,调制到在每个子信道上进行传输。正交信号可以通过在接收端采用相关技术来分开,这样可以减少子信道之间的相互干扰(ISI) 。每个子信道上的信号带宽小于信道的相关带宽,因此每个子信道上可以看成平坦性衰落,从而可以消除码间串扰,而且由于每个子信道的带宽仅仅是原信道带宽的一小部分,信道均衡变得相对容易。
OFDM技术是HPA联盟(HomePlug Powerline Alliance)工业规范的基础,它采用一种不连续的多音调技术,将被称为载波的不同频率中的大量信号合并成单一的信号,从而完成信号传送。由于这种技术具有在杂波干扰下传送信号的能力,因此常常会被利用在容易受外界干扰或者抵抗外界干扰能力较差的传输介质中。
峰值平均功率比(PAPR—Peak to Average Power Ratio),简称峰均比(PAPR)。MIMO-OFDM系统能够提供更大的覆盖范围、更好的传输质量、更高的数据速率和频谱效率。然而,由于OFDM 符号是由多个独立经过调制的子载波信号叠加而成的,当各个子载波相位相同或者相近时,叠加信号便会受到相同初始相位信号的调制,从而产生较大的瞬时功率峰值,由此进一步带来较高的峰值平均功率比(PAPR—Peak to Average Power Ratio),简称峰均比(PAPR)。由于一般的功率放大器的动态范围都是有限的,所以峰均比较大的MIMO-OFDM信号极易进入功率放大器的非线性区域,导致信号产生非线性失真,造成明显的频谱扩展干扰以及带内信号畸变,导致整个系统性能严重下降。高峰均比已成为MIMO-OFDM 的一个主要技术阻碍。
OFDM(Orthogonal Frequency Division Multiplexing)正交频分复用技术,OFDM是一种MCM(Multi-Carrier Modulation)多载波调制技术。其核心是将信道分成若干个正交子信道,在每个子信道上进行窄带调制和传输,这样减少了子信道之间的相互干扰。每个子信道上的信号带宽小于信道的相关带宽,因此每个子信道上的频率选择性衰落是平坦的,大大消除了符号间干扰。另外,由于在OFDM系统中各个子信道的载波相互正交,于是它们的频谱是相互重叠的,这样不但减小了子载波间的相互干扰,同时又提高了频谱利用率。在各个子信道中的这种正交调制和解调可以采用IFFT和FFT方法来实现。
作为OFDM系统的主要问题之一的高峰值平均功率比问题一直是学术和工 业界的研究重点。迄今为止,人们已经提出了很多的解决办法, 这些方法大致 分为三大类:
(1)限幅类技术, 如幅度切削和滤波,峰值加窗技术和峰值抵消技术。
(2)编码类技术, 如块编码, Golay互补序列和Reed-Muller码 。
(3)概率类技术。如选择性映射(SLM,Selected Mapping) ,部分传输序 列(PTS,Partial Transmit Sequence) ,子载波保留方法(TR, Tone Reservation) ,子载波注入方法(TI,Tone Injection) [60]和活动 星座扩展方法(ACE,Active Constellation Expansion) 等方法, 但是这 些方法都存在着各种各样的缺点。
在业界,往往采用最简单的限幅滤波类技术 来降低PAPR,这种方法虽然简单,但是它降低了系统的误比特率,同时引入 了带外噪声和带内失真。编码类技术是另一个著名的PAPR减少方法,它获得 了最好的PAPR减少,但是它的解码复杂度太高,码率太低,因此这种技术只 适用于子载波数较小的情形(N ≤ 32)。概率类技术不着眼于降低信号幅度的最大值,而是降低峰值出现的概率。以SLM,PTS,TR和TI为代表。SLM技术 需要多个IFFT运算,因此该方法的复杂度较高。PTS技术为了获得最优的相位 旋转因子,搜索的复杂度随OFDM子块数呈指数增长。而且这两种方法都需要 发送边信息。TR技术的最优峰值减少子载波的选取和最优切削阈值的选取是 非常困难的。TI技术需要修正或扩展信号的调制星座,使得同一个数据对应星 座上的多个点,但选取最优的信号星座表示也是非常困难的。
参数化最小互熵(PMCE,Parametric Minimum Cross-Entropy) 方法起 源于著名的Kullback最小互熵方法(M inxEnt) 。主要用于稀有事件的概率 估计和对可满足性问题的计数。这种方法是基于由最优联合MinxEnt分布推导 而来的边缘概率分布。类似于互熵(CE,Cross Entropy)方法,PMCE方法 首先把一个基本的计数问题转化为一个相应的稀有事件出现的概率估计问题, 然后解这个估计问题。PMCE方法能发现重要采样分布的最优参数,并能高 效地给出高质量的解。它是一个多项式时间算法。

二、核心程序
相位表格如下:
Phase_choice = ...
[1 1 1 1 1 1 1 1;
1 1 1 1 1 1 1 2;
1 1 1 1 1 1 2 1;
1 1 1 1 1 1 2 2;
1 1 1 1 1 2 1 1;
1 1 1 1 1 2 1 2;
1 1 1 1 1 2 2 1;
1 1 1 1 1 2 2 2;
1 1 1 1 2 1 1 1;
1 1 1 1 2 1 1 2;
1 1 1 1 2 1 2 1;
1 1 1 1 2 1 2 2;
1 1 1 1 2 2 1 1;
1 1 1 1 2 2 1 2;
1 1 1 1 2 2 2 1;
1 1 1 1 2 2 2 2;
1 1 1 2 1 1 1 1;
1 1 1 2 1 1 1 2;
1 1 1 2 1 1 2 1;
1 1 1 2 1 1 2 2;
1 1 1 2 1 2 1 1;
1 1 1 2 1 2 1 2;
1 1 1 2 1 2 2 1;
1 1 1 2 1 2 2 2;
1 1 1 2 2 1 1 1;
1 1 1 2 2 1 1 2;
1 1 1 2 2 1 2 1;
1 1 1 2 2 1 2 2;
1 1 1 2 2 2 1 1;
1 1 1 2 2 2 1 2;
1 1 1 2 2 2 2 1;
1 1 1 2 2 2 2 2;
1 1 2 1 1 1 1 1;
1 1 2 1 1 1 1 2;
1 1 2 1 1 1 2 1;
1 1 2 1 1 1 2 2;
1 1 2 1 1 2 1 1;
1 1 2 1 1 2 1 2;
1 1 2 1 1 2 2 1;
1 1 2 1 1 2 2 2;
1 1 2 1 2 1 1 1;
1 1 2 1 2 1 1 2;
1 1 2 1 2 1 2 1;
1 1 2 1 2 1 2 2;
1 1 2 1 2 2 1 1;
1 1 2 1 2 2 1 2;
1 1 2 1 2 2 2 1;
1 1 2 1 2 2 2 2;
1 1 2 2 1 1 1 1;
1 1 2 2 1 1 1 2;
1 1 2 2 1 1 2 1;
1 1 2 2 1 1 2 2;
1 1 2 2 1 2 1 1;
1 1 2 2 1 2 1 2;
1 1 2 2 1 2 2 1;
1 1 2 2 1 2 2 2;
1 1 2 2 2 1 1 1;
1 1 2 2 2 1 1 2;
1 1 2 2 2 1 2 1;
1 1 2 2 2 1 2 2;
1 1 2 2 2 2 1 1;
1 1 2 2 2 2 1 2;
1 1 2 2 2 2 2 1;
1 1 2 2 2 2 2 2;
1 2 1 1 1 1 1 1;
1 2 1 1 1 1 1 2;
1 2 1 1 1 1 2 1;
1 2 1 1 1 1 2 2;
1 2 1 1 1 2 1 1;
1 2 1 1 1 2 1 2;
1 2 1 1 1 2 2 1;
1 2 1 1 1 2 2 2;
1 2 1 1 2 1 1 1;
1 2 1 1 2 1 1 2;
1 2 1 1 2 1 2 1;
1 2 1 1 2 1 2 2;
1 2 1 1 2 2 1 1;
1 2 1 1 2 2 1 2;
1 2 1 1 2 2 2 1;
1 2 1 1 2 2 2 2;
1 2 1 2 1 1 1 1;
1 2 1 2 1 1 1 2;
1 2 1 2 1 1 2 1;
1 2 1 2 1 1 2 2;
1 2 1 2 1 2 1 1;
1 2 1 2 1 2 1 2;
1 2 1 2 1 2 2 1;
1 2 1 2 1 2 2 2;
1 2 1 2 2 1 1 1;
1 2 1 2 2 1 1 2;
1 2 1 2 2 1 2 1;
1 2 1 2 2 1 2 2;
1 2 1 2 2 2 1 1;
1 2 1 2 2 2 1 2;
1 2 1 2 2 2 2 1;
1 2 1 2 2 2 2 2;
1 2 2 1 1 1 1 1;
1 2 2 1 1 1 1 2;
1 2 2 1 1 1 2 1;
1 2 2 1 1 1 2 2;
1 2 2 1 1 2 1 1;
1 2 2 1 1 2 1 2;
1 2 2 1 1 2 2 1;
1 2 2 1 1 2 2 2;
1 2 2 1 2 1 1 1;
1 2 2 1 2 1 1 2;
1 2 2 1 2 1 2 1;
1 2 2 1 2 1 2 2;
1 2 2 1 2 2 1 1;
1 2 2 1 2 2 1 2;
1 2 2 1 2 2 2 1;
1 2 2 1 2 2 2 2;
1 2 2 2 1 1 1 1;
1 2 2 2 1 1 1 2;
1 2 2 2 1 1 2 1;
1 2 2 2 1 1 2 2;
1 2 2 2 1 2 1 1;
1 2 2 2 1 2 1 2;
1 2 2 2 1 2 2 1;
1 2 2 2 1 2 2 2;
1 2 2 2 2 1 1 1;
1 2 2 2 2 1 1 2;
1 2 2 2 2 1 2 1;
1 2 2 2 2 1 2 2;
1 2 2 2 2 2 1 1;
1 2 2 2 2 2 1 2;
1 2 2 2 2 2 2 1;
1 2 2 2 2 2 2 2;
2 1 1 1 1 1 1 1;
2 1 1 1 1 1 1 2;
2 1 1 1 1 1 2 1;
2 1 1 1 1 1 2 2;
2 1 1 1 1 2 1 1;
2 1 1 1 1 2 1 2;
2 1 1 1 1 2 2 1;
2 1 1 1 1 2 2 2;
2 1 1 1 2 1 1 1;
2 1 1 1 2 1 1 2;
2 1 1 1 2 1 2 1;
2 1 1 1 2 1 2 2;
2 1 1 1 2 2 1 1;
2 1 1 1 2 2 1 2;
2 1 1 1 2 2 2 1;
2 1 1 1 2 2 2 2;
2 1 1 2 1 1 1 1;
2 1 1 2 1 1 1 2;
2 1 1 2 1 1 2 1;
2 1 1 2 1 1 2 2;
2 1 1 2 1 2 1 1;
2 1 1 2 1 2 1 2;
2 1 1 2 1 2 2 1;
2 1 1 2 1 2 2 2;
2 1 1 2 2 1 1 1;
2 1 1 2 2 1 1 2;
2 1 1 2 2 1 2 1;
2 1 1 2 2 1 2 2;
2 1 1 2 2 2 1 1;
2 1 1 2 2 2 1 2;
2 1 1 2 2 2 2 1;
2 1 1 2 2 2 2 2;
2 1 2 1 1 1 1 1;
2 1 2 1 1 1 1 2;
2 1 2 1 1 1 2 1;
2 1 2 1 1 1 2 2;
2 1 2 1 1 2 1 1;
2 1 2 1 1 2 1 2;
2 1 2 1 1 2 2 1;
2 1 2 1 1 2 2 2;
2 1 2 1 2 1 1 1;
2 1 2 1 2 1 1 2;
2 1 2 1 2 1 2 1;
2 1 2 1 2 1 2 2;
2 1 2 1 2 2 1 1;
2 1 2 1 2 2 1 2;
2 1 2 1 2 2 2 1;
2 1 2 1 2 2 2 2;
2 1 2 2 1 1 1 1;
2 1 2 2 1 1 1 2;
2 1 2 2 1 1 2 1;
2 1 2 2 1 1 2 2;
2 1 2 2 1 2 1 1;
2 1 2 2 1 2 1 2;
2 1 2 2 1 2 2 1;
2 1 2 2 1 2 2 2;
2 1 2 2 2 1 1 1;
2 1 2 2 2 1 1 2;
2 1 2 2 2 1 2 1;
2 1 2 2 2 1 2 2;
2 1 2 2 2 2 1 1;
2 1 2 2 2 2 1 2;
2 1 2 2 2 2 2 1;
2 1 2 2 2 2 2 2;
2 2 1 1 1 1 1 1;
2 2 1 1 1 1 1 2;
2 2 1 1 1 1 2 1;
2 2 1 1 1 1 2 2;
2 2 1 1 1 2 1 1;
2 2 1 1 1 2 1 2;
2 2 1 1 1 2 2 1;
2 2 1 1 1 2 2 2;
2 2 1 1 2 1 1 1;
2 2 1 1 2 1 1 2;
2 2 1 1 2 1 2 1;
2 2 1 1 2 1 2 2;
2 2 1 1 2 2 1 1;
2 2 1 1 2 2 1 2;
2 2 1 1 2 2 2 1;
2 2 1 1 2 2 2 2;
2 2 1 2 1 1 1 1;
2 2 1 2 1 1 1 2;
2 2 1 2 1 1 2 1;
2 2 1 2 1 1 2 2;
2 2 1 2 1 2 1 1;
2 2 1 2 1 2 1 2;
2 2 1 2 1 2 2 1;
2 2 1 2 1 2 2 2;
2 2 1 2 2 1 1 1;
2 2 1 2 2 1 1 2;
2 2 1 2 2 1 2 1;
2 2 1 2 2 1 2 2;
2 2 1 2 2 2 1 1;
2 2 1 2 2 2 1 2;
2 2 1 2 2 2 2 1;
2 2 1 2 2 2 2 2;
2 2 2 1 1 1 1 1;
2 2 2 1 1 1 1 2;
2 2 2 1 1 1 2 1;
2 2 2 1 1 1 2 2;
2 2 2 1 1 2 1 1;
2 2 2 1 1 2 1 2;
2 2 2 1 1 2 2 1;
2 2 2 1 1 2 2 2;
2 2 2 1 2 1 1 1;
2 2 2 1 2 1 1 2;
2 2 2 1 2 1 2 1;
2 2 2 1 2 1 2 2;
2 2 2 1 2 2 1 1;
2 2 2 1 2 2 1 2;
2 2 2 1 2 2 2 1;
2 2 2 1 2 2 2 2;
2 2 2 2 1 1 1 1;
2 2 2 2 1 1 1 2;
2 2 2 2 1 1 2 1;
2 2 2 2 1 1 2 2;
2 2 2 2 1 2 1 1;
2 2 2 2 1 2 1 2;
2 2 2 2 1 2 2 1;
2 2 2 2 1 2 2 2;
2 2 2 2 2 1 1 1;
2 2 2 2 2 1 1 2;
2 2 2 2 2 1 2 1;
2 2 2 2 2 1 2 2;
2 2 2 2 2 2 1 1;
2 2 2 2 2 2 1 2;
2 2 2 2 2 2 2 1;
2 2 2 2 2 2 2 2;
];............................................................................
PAPR_pts = zeros(1,Nframes);
PAPRA = 7.5:0.25:10;
for ii = 1:length(Iter)
ii
for k=1:Nframes
%产生数据源
QPSK_Ind = randint(1,Nfft,length(Map_qpsk)) + 1;
%调制,这里为了研究PAPR性能,所以不加入编码模块和交织模块
Qpsk_mod = Map_qpsk(QPSK_Ind(1,:));
%进行IFFT变换
Dat_Ifft = ifft(Qpsk_mod,[],2);
%计算功率和PAPR
Signal_Power = abs(Dat_Ifft.^2);
Peak_Power = max(Signal_Power,[],2);
Mean_Power = mean(Signal_Power,2);
PAPRo(k) = 10*log10(Peak_Power./Mean_Power);
%随机分块
QPSK_Ind = randperm(Nfft);
A = zeros(Npts,Nfft);
for v=1:Npts
A(v,QPSK_Ind(v:Npts:Nfft)) = Qpsk_mod(QPSK_Ind(v:Npts:Nfft));
end
a = ifft(A,[],2);
%限幅
Tho = mean2(abs(a));
[rr,cc] = size(a);
for i = 1:rr
for j = 1:cc
if abs(a(i,j)) > Tho
a(i,j) = Tho*(real(a(i,j)) + ij*imag(a(i,j)))/abs(a(i,j));
end
end
end
%PCME算法
P0 = 0.5*ones(1,Npts);%初始概率为0.5
Ps = zeros(Iter(ii),Npts);
P = zeros(Iter(ii),Npts);
for iter = 1:Iter(ii)
...............................................................
%更新概率P
if iter == 1
Ps(iter,:) = P0;
else
Ps(iter,:) = alpha * P(iter,:) + (1-alpha) * P(iter-1,:);
if sum(Ps(iter,:)) == round(sum(Ps(iter,:)));
break;
end
end
end
%根据PMCE计算得到的相位因子来计算PAPR值
aa = sum(a.*repmat(sign((1-2*Ps(iter,:)))',1,Nfft));
Signal_Power = abs(aa.^2);
Peak_Power_temp = max(Signal_Power,[],2);
Mean_Power_temp = mean(Signal_Power,2);
PAPR_temp(k) = 10*log10(Peak_Power_temp./Mean_Power_temp);
end
[cdf,PAPR] =ecdf(PAPR_temp);
NUMs(ii) = mean(PAPR);
end
figure;
plot(Iter,NUMs,'b-o');
xlabel('PAPR0[dB]');
ylabel('Search');
grid on;
%01-62三、测试结果
在matlab2021a中仿真得到如下的效果:
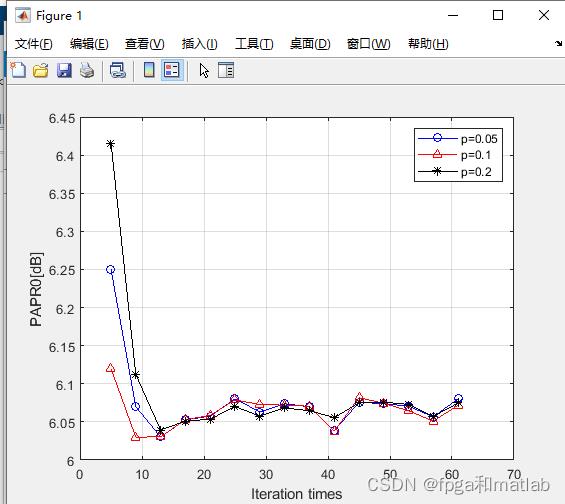
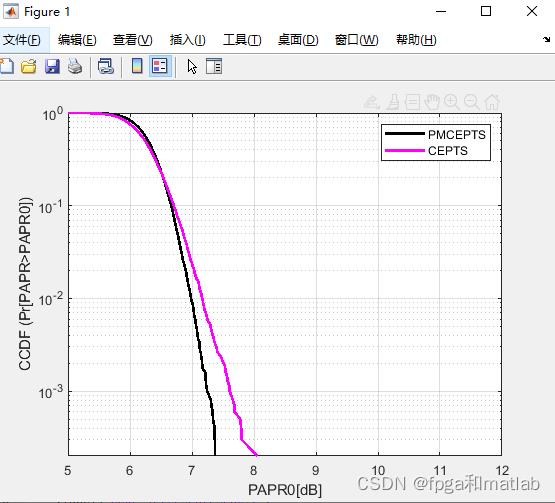
以上是关于基于参数化最小互熵(Parametric Minimum Cross Entropy,PMCE)算法的PAPR抑制matlab仿真的主要内容,如果未能解决你的问题,请参考以下文章