基础篇9 # 排序:冒泡排序(Bubble Sort)插入排序(Insertion Sort)选择排序(Selection Sort)
Posted 凯小默
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基础篇9 # 排序:冒泡排序(Bubble Sort)插入排序(Insertion Sort)选择排序(Selection Sort)相关的知识,希望对你有一定的参考价值。
说明
【数据结构与算法之美】专栏学习笔记
如何分析一个排序算法?
1、排序算法的执行效率
- 最好情况、最坏情况、平均情况时间复杂度
- 时间复杂度的系数、常数 、低阶
- 比较次数和交换(或移动)次数
2、排序算法的内存消耗
3、排序算法的稳定性
原地排序(Sorted in place):就是特指空间复杂度是 O(1) 的排序算法。
稳定性度量指标:如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变,这种排序算法叫作稳定的排序算法;如果前后顺序发生变化,那对应的排序算法就叫作不稳定的排序算法。
冒泡排序(Bubble Sort)
冒泡排序是一种简单的排序算法,它重复地走访过要排序的数列,每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。
// 冒泡排序,a表示数组,n表示数组大小
public void bubbleSort(int[] a, int n)
if (n <= 1) return;
for (int i = 0; i < n; ++i)
// 提前退出冒泡循环的标志位
boolean flag = false;
for (int j = 0; j < n - i - 1; ++j)
if (a[j] > a[j+1]) // 交换
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = true; // 表示有数据交换
if (!flag) break; // 没有数据交换,提前退出
可以查看排序的可视化演示

有序度
有序度是数组中具有有序关系的元素对的个数。
有序元素数学表达式表示如下:
有序元素对:a[i] <= a[j], 如果 i < j。
比如:2,4,3,1,5,6,这组数据
有序元素有:
(2, 4) (2, 3) (2, 5) (2, 6)
(4, 5) (4, 6)
(3, 5) (3, 6)
(1, 5) (1, 6)
(5, 6)
所以上面数据组的有序度就是11。
比如 6,5,4,3,2,1,有序度是 0;对于一个完全有序的数组,有序度就是 n(n-1)/2*。全有序的数组的有序度叫作满有序度。
逆序度
逆序元素对:a[i] > a[j], 如果i < j。
逆序度 = 满有序度 - 有序度。
下面用 4,5,6,3,2,1 这组数据来对比一下冒泡过程的有序度跟逆序度:
| 冒泡次数 | 冒泡后结果 | 有序度 | 逆序度 |
|---|---|---|---|
| 初始状态 | 4,5,6,3,2,1 | 3 | 12 |
| 第 1 次冒泡 | 4,5,3,2,1,6️⃣ | 6 | 9 |
| 第 2 次冒泡 | 4,3,2,1,5️⃣,6️⃣ | 9 | 6 |
| 第 3 次冒泡 | 3,2,1,4️⃣,5️⃣,6️⃣ | 12 | 3 |
| 第 4 次冒泡 | 2,1,3️⃣,4️⃣,5️⃣,6️⃣ | 14 | 1 |
| 第 5 次冒泡 | 1,2️⃣,3️⃣,4️⃣,5️⃣,6️⃣ | 15 | 0 |
冒泡排序包含两个操作原子,比较和交换。每交换一次,有序度就加 1。对于包含 n 个数据的数组进行冒泡排序,平均情况下,需要 n*(n-1)/4 次交换操作,平均情况下的时间复杂度就是 O( n 2 n^2 n2)。
插入排序(Insertion Sort)
插入排序是一种简单的排序算法,它的基本思想是:将一个记录插入到已排好序的有序表中,从而得到一个新的记录数增1的有序表。
插入算法的核心思想:将数组中的数据分为已排序区间和未排序区间两个区间,然后初始已排序区间只有一个元素,就是数组的第一个元素。再取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。
例子:4,5,6,1,3,2 数据进行插入排序,逆序数为10。

插入排序包含两种操作,一种是元素的比较,一种是元素的移动,移动操作的次数总是固定的,就等于逆序度。
// 插入排序,a表示数组,n表示数组大小
public void insertionSort(int[] a, int n)
if (n <= 1) return;
for (int i = 1; i < n; ++i)
int value = a[i];
int j = i - 1;
// 查找插入的位置
for (; j >= 0; --j)
if (a[j] > value)
a[j+1] = a[j]; // 数据移动
else
break;
a[j+1] = value; // 插入数据
有点晕的同学可以查看排序的可视化演示,选择插入排序,就能清晰的看到过程效果
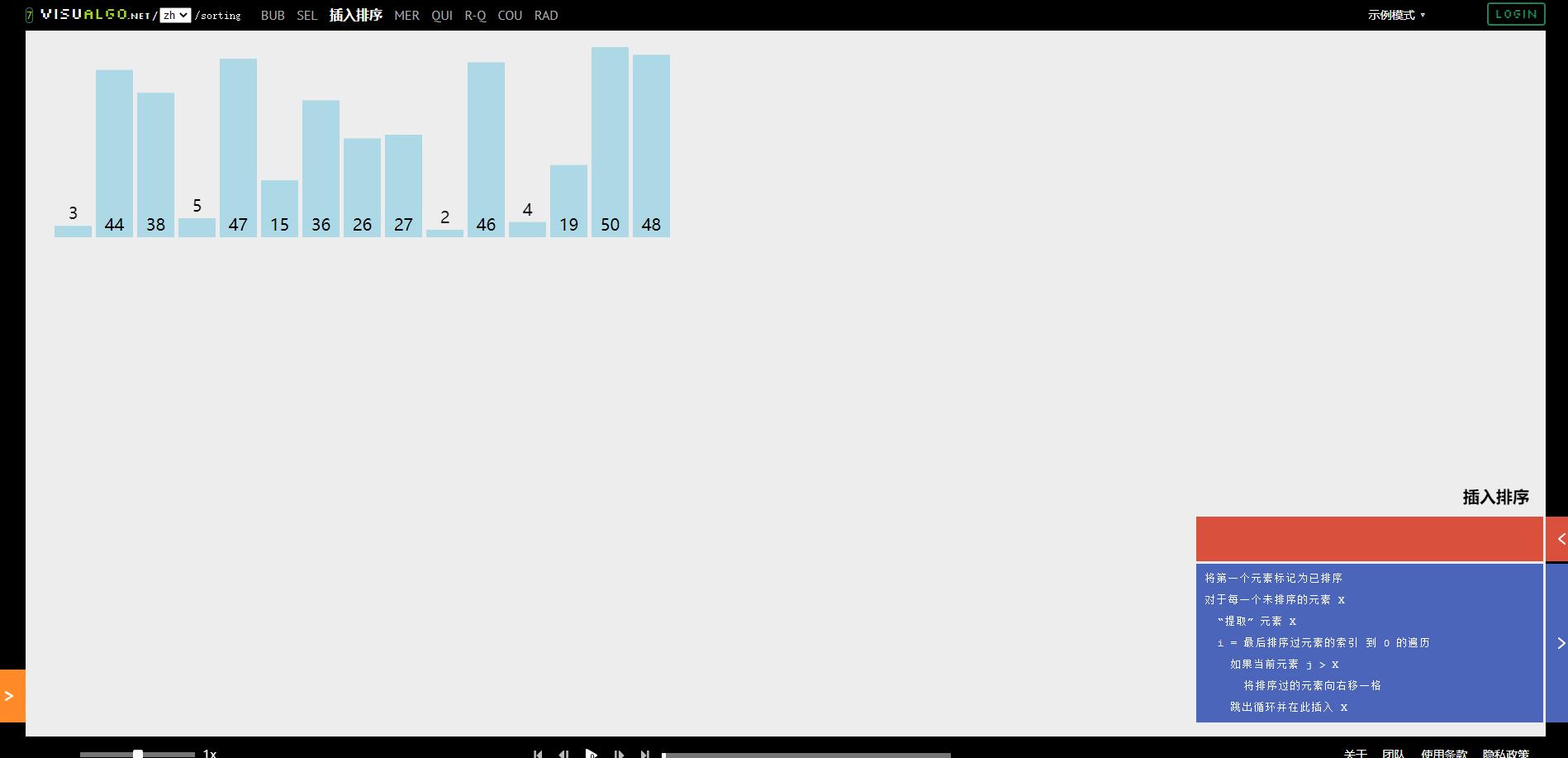
现实生活里就有这样的例子,打扑克的时候,整理牌用到的思路其实就是插入排序,牌堆就是未排序区间,手中已摸的牌就是已排序区间。每一次抽牌,就根据摸到的牌的大小从左往右,或者从右往左对比,放到恰当的位置。
选择排序(Selection Sort)
选择排序算法的实现思路有点类似插入排序,但选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。
选择排序原理示意图:可以查看排序的可视化演示,选择选择排序,就能清晰的看到过程效果
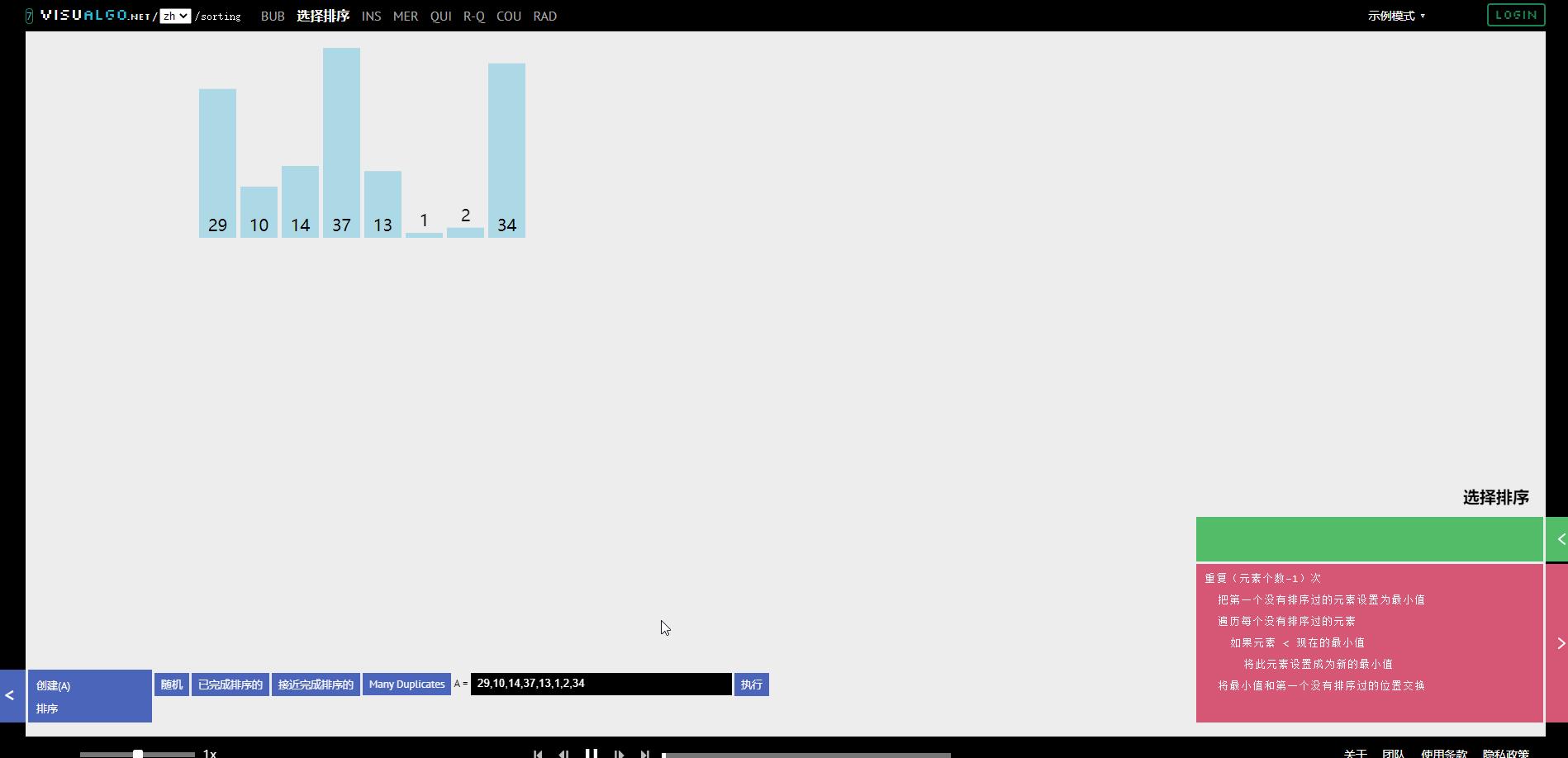
总结
总的来说,冒泡排序的数据交换要比插入排序的数据移动要复杂,相对于冒泡排序和插入排序,选择排序不稳定,就稍微逊色一点。
| 空间复杂度 | 是否原地排序 | 是否稳定 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(1) | ✔️ | ✔️ | O(n) | O( n 2 n^2 n2) | O( n 2 n^2 n2) |
| 插入排序 | O(1) | ✔️ | ✔️ | O(n) | O( n 2 n^2 n2) | O( n 2 n^2 n2) |
| 选择排序 | O(1) | ✔️ | ❌ | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O( n 2 n^2 n2) |
以上是关于基础篇9 # 排序:冒泡排序(Bubble Sort)插入排序(Insertion Sort)选择排序(Selection Sort)的主要内容,如果未能解决你的问题,请参考以下文章