2023年数学建模美赛A题（A drought stricken plant communities）分析与编程

Posted 2023-03-05 YouCans

2023年数学建模美赛A题（A drought stricken plant communities）分析与编程
2023年数学建模美赛D题（Prioritizing the UN Sustainability Goals）分析与编程

特别提示：
1 本文介绍2023年美赛题目，进行深入分析；
2 本文首先对 A题进行深入分析，其它题目分析详见专题讨论；
3 最新更新：增加了多种群LK模型和例程。

文章目录

• 2023年数学建模美赛A题（A drought stricken plant communities）分析与编程
• • 1. A题：A drought stricken plant communities（遭受旱灾的植物群落）
  • • 1.1 背景
    • 1.2 要求
  • 2. 问题分析
  • 3. 种间竞争关系理论 Lotka-Volterra模型
  • • 3.1 Malthus人口理论
    • 3.2 捕食者-猎物系统
    • 3.3 Lotka-Volterra模型
    • 3.4 Lotka-Volterra模型的数值模拟
    • 3.4 三种群 Lotka-Volterra模型的数值模拟
  • 4. Lotka-Volterra模型与全球植被模式
  • • 4.1 现存生物量一般动力学模型
    • 4.2 包含n个物种的全球植被模式的一般动力学方程：
  • 5. 参考数据
  • 6. 参考资料
  • 3. 微分方程模型求解
  • • 3.1 基本概念
    • 3.2 微分方程的数学建模
    • 3.3 微分方程的数值解法
  • 4. SciPy 求解常微分方程（组）
  • • 4.1 一阶常微分方程（组）模型
    • 4.2 scipy.integrate.odeint() 函数
  • 5. 求洛伦兹（Lorenz）方程的数值解
  • • 6.1 例题 2：求洛伦兹（Lorenz）方程的数值解
    • 6.2 洛伦兹（Lorenz）方程问题的编程步骤
    • 6.3 洛伦兹（Lorenz）方程问题 Python 例程
    • 6.4 洛伦兹（Lorenz）方程问题 Python 例程运行结果

2023年数学建模美赛A题（A drought stricken plant communities）分析与编程

1. A题：A drought stricken plant communities（遭受旱灾的植物群落）

1.1 背景

不同的植物群落对压力的反应不同。例如，草原对干旱非常敏感。干旱发生的频率和严重程度不同。但大量的观察表明，不同物种的数量对植物群落如何在连续多代干旱周期中的适应能力起到了重要作用。在一些仅有单一物种的植物群落中，后代不像有 4种或更多物种的群落中的个体植物那样容易适应干旱条件。这些观察引出了许多问题：例如，对于一个植物群落，要从这种局部生物多样性中受益，最少需要多少种物种？随着物种数量的增加，这种现象如何发展？这对植物群落的长期生存性意味着什么？

1.2 要求

考虑到植物群落中干旱适应性与物种数量的关系，您的任务是探索和更好地理解这一现象。具体地，您应该：

• 开发一个数学模型，预测植物群落随着不同的不规则天气周期的变化。在降水充足的时期应包括降雨的时间。该模型应考虑干旱周期中不同物种之间的相互作用。

• 探讨你能从你的模型中得出什么结论，关于植物群体与更大环境的长期相互作用。考虑以下问题：

  • 要使植物群落受益，需要的不同植物物种数量是多少，随着物种数量的增加会发生什么？
  • 社区中的物种类型如何影响你的结果？
  • 未来天气周期中干旱发生的频率和变化范围的影响是什么？如果干旱较少，物种数量对总人口的影响是否相同？
  • 污染和栖息地减少等其他因素如何影响你的结论？
  • 您的模型表明应该采取什么措施以确保植物群落的长期生存力，对更大环境的影响是什么？

2. 问题分析

1. 这是一道微分方程建模题目，建立模型是关键，模型求解并不难，基于模型的分析和讨论可以发挥想象力。
2. 需要先找到相关研究论文，根据论文中提出物种与环境的关系的原理模型，建立微分方程的数学模型。论文中会给出具体的数学模型，可能是偏微分方程，能够求解就直接用；如果不会就简化为常微分方程也可以。
3. 微分方程是描述系统的状态随时间和空间演化的数学工具。本题显然是研究几种物种的数量随时间的变化规律。
4. **特别注意：**给定初始条件的一阶常微分方程（组）的标准形式是：
   $$\{\begin{array}{l}\begin{array}{rl}& \frac{dy}{dt}=f(y,t)\\ & y(t_0)=y_0\end{array}\end{array}$$
   微分方程是微分方程组，式中的 y 是数组向量，有几个物种就有几个变量，$y_i(t)$ 表示物种 i 的总量随时间 t 的变化。
   也就是说，可以先建立一种或两种物种的模型，分析变化趋势，再依次增多物种数量，分析变化趋势。
5. **特别注意：**构造外部条件及降雨量随时间的变化函数。
   降雨量函数要满足题目要求：（1）不同的不规则天气周期，既要有干旱周期，又要有降水周期，还要有间隔周期；（2）干旱发生的频率和变化范围。
   如何构造合理的降雨量函数，可以体现能力和创新的。思路一是设计的降雨量函数包含不同的可能模式，思路二是降雨量函数包括地球上典型的干旱模式，思路三是找到非洲地区的降雨量统计。
6. **特别注意：**污染和栖息地减少等其他因素的影响，需要在模型中增加一个系数，或者一项，反映污染和栖息地减少的影响。直接在模型中增加一个系数，比较简单。
   进一步地，可以构思污染与种群总数相关，是一个随种群总数变化的系数。
7. **特别注意：**采取什么措施以确保植物群落的长期生存力，应该通过模型研究得到结论。
   建议首先查找资料找到一种或多种靠谱的措施，然后将其量化为一个系数或一项加入模型（跟污染系数的原理是一致的），通过模型研究措施的影响，证明采取的措施是有效的。
   简单地，既然污染会破坏环境，那么防止污染就可以保护环境，可以抑制污染系数的增大。
   又如，水土保持能否量化为模型参数？食物链能否构造模型？
8. 微分方程模型求解，详见本文后续章节及博客：

• Python小白的数学建模课-09.微分方程模型（https://youcans.blog.csdn.net/article/details/117702996）
• Python小白的数学建模课-11.偏微分方程数值解法（https://youcans.blog.csdn.net/article/details/119755450）
  本题要研究时间的变化，因此跟微分方程边值问题没什么关系。

---

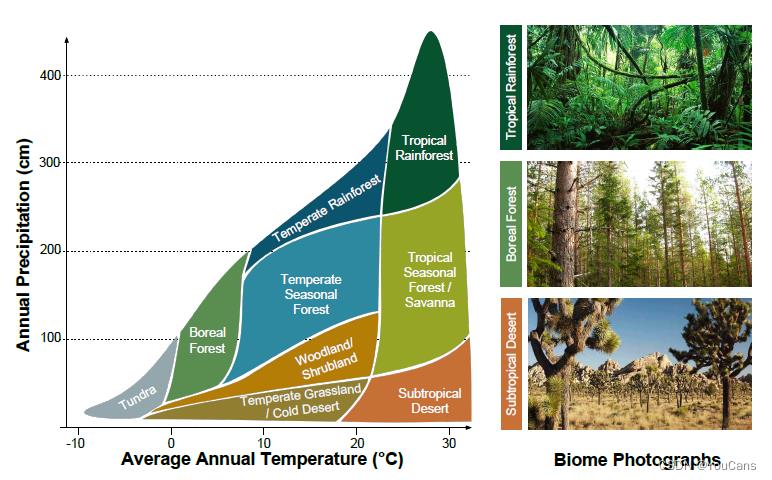
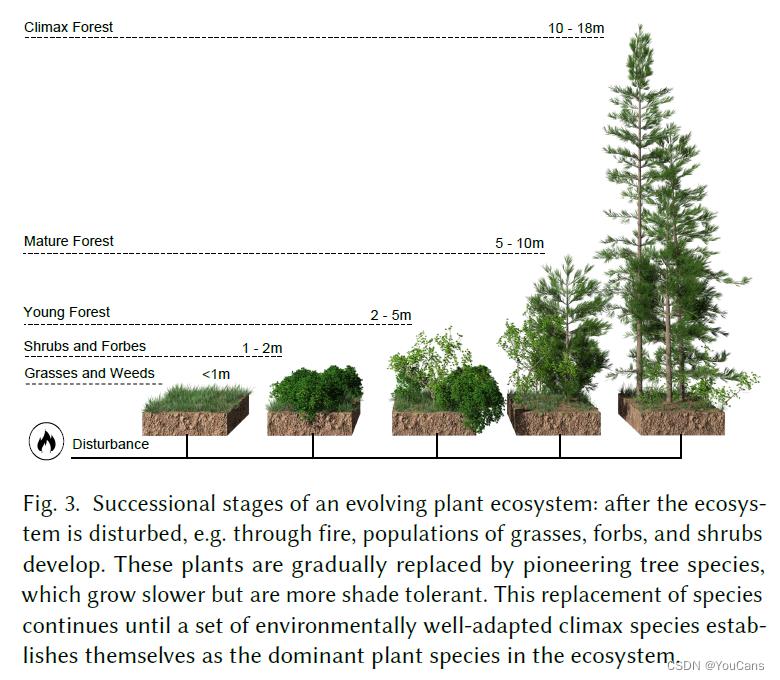
3. 种间竞争关系理论 Lotka-Volterra模型

常微分方程与生态学有什么关联？生态学理论一直以种群动态为根基。它涌现出所谓生物多样性、空间分布格局、种间互作，也是功能性状、物候等话题在应用生态学中的归宿。

3.1 Malthus人口理论

1798年Malthus提出的人口理论被认为是生态学第一定律。Malthus指出，一切生物在“不受外力”的影响下，都以恒定的速率 k 增长。用微分方程可表达为：
$$\frac{dx}{dt}=kx,k>0$$

该方程可直接用定积分（或不定积分）求解，结果为：
$$x=e^{k(t-t_0)}{x}_0$$
这是一个指数曲线， 称为**「自然繁殖（normal reproduction）** 。

由于资源有限，当种群个体数过大时竞争激烈，故种群增长率会有所下降。所以 k 不是一个恒值，而是关于 x 的函数：
$$k=f(x)$$

函数f(x)应当是在x>0范围内随x增加而单调递减的函数。根据麦克劳林展开式：

$$f(x)=f(0)+\frac{df(x)}{dx}{|}_{x=0}(x)+o(x)\approx a-bx$$

当x足够小时，任何光滑函数可用线性函数作近似，因此:

$$\frac{dx}{dt}=(a-bx)x$$

求解微分方程，可得：

$$x=\frac{a}{e^{-at}+b}$$

3.2 捕食者-猎物系统

Lotka（1910）和Volterra（1926）分别提出了捕食者–猎物系统的种群动态模型，称为Lotka–Volterra模型。该模型假设：捕食者、猎物相遇的几率与双方的种群个体数成正比；捕食者捕食猎物的频次与相遇频次成正比；捕食者种群增长率与捕食猎物的频次成正比；捕食者以恒定的速率死亡。
$$\begin{gathered} \frac{dx}{dt}=kx-axy \\ \frac{dy}{dt}=-ly+bxy \end{gathered}$$

这个二元系统（捕食者+猎物）动态会如何变化：

► 捕食者、猎物种群动态的相位曲线如何？

► 捕食者、猎物种群动态是达到稳定平衡，还是有限环，还是混沌？或者说，相位曲线会呈螺旋形，造成系统崩溃或收敛到一个稳定点？

► 受到外界扰动时，捕食者、猎物种群动态还能保持稳定吗？

1 为什么到达平衡的时间经常是无穷大？

2 初值对Lotka–Volterra模型行为的影响

3 无扰动下Lotka–Volterra有限环大小不变

3.3 Lotka-Volterra模型

Lotka-Volterra模型（Lotka-Volterra种间竞争模型）是logistic模型（阻滞增长模型）的延伸。现设定如下参数：

• N1、N2：分别为两个物种的种群数量
• K1、K2：分别为两个物种的环境容纳量
• r1、r2 ：分别为两个物种的种群增长率

依逻辑斯蒂模型有如下关系：
$$\frac{d{N}_1}{dt}=r_1\ast N_1\ast (1-\frac{N_1}{K_1})$$

其中：N/K 可以理解为已经利用的空间（称为“已利用空间项”），则 $(1-N/K)$ 可以理解为尚未利用的空间（称为“未利用空间项”）。
当两个物种竞争或者利用同一空间时，“已利用空间项”还应该加上N2种群对空间的占用。则：
KaTeX parse error: Undefined control sequence: \\alfa at position 53: …acN_1K_1 - \\̲a̲l̲f̲a̲ ̲\\fracN_2K_2…

其中，α：物种2对物种1的竞争系数，即每个N2个体所占用的空间相当于α个N1个体所占用空间。
则有，β：物种1对物种2的竞争系数，即每个N1个体所占用的空间相当于β个N2个体所占用空间。则另有：

$$\frac{d{N}_2}{dt}=r_2\ast N_2\ast (1-\frac{N_2}{K_2}-\beta \frac{N_1}{K_1})$$

当物种N1种群（物种1）的环境容纳量为K1时，N1种群中每个个体对自身种群的增长抑制作用为1/K1；
同理，N2种群中每个个体对自身种群的增长抑制作用为1/K2。
另外，从（1）、（2）两个方程以及α、β的定义中可知：

• N2种群中每个个体对N1种群的影响为：α/K1
• N1种群中每个个体对N2种群的影响为：β/K2
  因此，当物种2可以抑制物种1时，可以认为，物种2对物种1的影响 > 物种2对自身的影响，即 α/K1 > 1/K2。
  整理后得：K2 > K1/α，同理有：
• 物种2不能抑制物种1：K2 < K1/α
• 物种1可以抑制物种2：K1 > K2/β
• 物种1不能抑制物种2：K1 < K2/β

在竞争的过程中，由于K1、K2、α 以及 β 的数值不同，可能会产生如下四种结果：
（1）物种1能抑制物种2，物种2能抑制物种1：两物种都有可能得胜；
（2）物种1不能抑制物种2，物种2能抑制物种1：物种 2 得胜；
（3）物种1能抑制物种2，物种2不能抑制物种1：物种 2 得胜；
（4）物种1不能抑制物种2，物种2不能抑制物种1：两物种都不能抑制对方，形成稳定平衡。
结果4是一个稳定的平衡，无论N1和N2种群数量的组合(N1,N2)落在直角坐标系内哪一区域，最终都将使得N1种群和N2种群的数量趋向平衡点。

3.4 Lotka-Volterra模型的数值模拟

引入如下的相对种群规模变量

$$
u=\\fracUU^∗=\\fraceγβU\\

v=\\fracVV^∗=\\fracγaV\\
$$

以及无量纲时间 $\tau =\alpha \beta t$

原来的 Lotka-Volterra 方程组可以被改写成：

d u d