卷积降维与池化降维的对比分析

Posted 2023-03-04 算法与编程之美

1 问题

在学习深度学习中卷积网络过程中，有卷积层，池化层，全连接层等等，其中卷积层与池化层均可以对特征图降维，本次实验针对控制其他层次一致的情况下，使用卷积降维与池化降维进行对比分析，主要是看两种降维方式对精度的影响以，以及损失值的大小。与此同时还可以探究不同维度下对精度是否有影响。

2 方法

这里是所有的代码，每次只需要更改网络的模型，即使用卷积层，使其降维的维度最后是1x1、7x7、14x14，需要更改三次，其次是使用池化层降维，最后也需要达到1x1、7x7、14x14，这三种维度。

import torchvision from torchvision.transforms import ToTensor, transforms from torch.utils.data import DataLoader from torch import nn import torch from time import * import xlwt import matplotlib.pyplot as plt plt.rcParams['font.sans-serif']=['SimHei'] plt.rcParams['axes.unicode_minus']=False # 创建一个新的类继承nn.Module class MyNet(nn.Module):    # (5.2) 定义网络有哪些层，这些层都作为成员变量    def __init__(self):        super().__init__()        # 卷积        # in_channels输入 out_channels输出 kernel_size 卷积核 stride 步长        self.conv1 = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3, stride=1, padding=1, )        # [-,16,28,28] [B, C, H, W]  batch channel height weight        # self.max_pool1 = nn.MaxPool2d(2)        self.conv2 = nn.Conv2d(in_channels=16, out_channels=32, kernel_size=3, stride=2, padding=1, )        # self.max_pool2 = nn.MaxPool2d(2)        # self.conv3 = nn.Conv2d(in_channels=32, out_channels=64, kernel_size=4, stride=2, padding=1, )        # self.max_pool3 = nn.MaxPool2d(2)        # [-,32,28,28]        # 全连接        self.fc = nn.Linear(in_features=32 * 14 * 14, out_features=10)    # (5.3) 定义数据在网络中的流动    # x - 1x28x28  CxHxW C表示通道数，H表示图像高度，W表示图像宽度    def forward(self, x):        x = torch.relu(self.conv1(x))        # x = self.max_pool1(x)        x = torch.relu(self.conv2(x))        # x = self.max_pool2(x)        # x = torch.relu(self.conv3(x))        # x = self.max_pool3(x)        x = torch.flatten(x, 1) #! 默认从0维开始拉伸  如果不设置1的话 会吧batch也拉伸进去        # [B, C, H, W]        # 拉伸 C H W        out = torch.relu(self.fc(x))        return out # 训练网络 # loss_list:  统计每个周期的平均loss def train(dataloader, net, loss_fn, optimizer):    size = len(dataloader.dataset)    epoch_loss = 0.0    batch_num = len(dataloader)    net.train()    # 精度=原预测正确数量/总数    correct = 0    # 一个batch一个batch的训练网络    for batch_idx, (x, y) in enumerate(dataloader):        # --->        x, y = x.to(device), y.to(device)  # 在GPU上运行x,y        pred = net(x)        loss = loss_fn(pred, y)        # 基于loss信息利用优化器从后向前更新网络全部参数        optimizer.zero_grad()        loss.backward()        optimizer.step()        epoch_loss += loss.item()        correct += (pred.argmax(1) == y).type(torch.float).sum().item()        if batch_idx % 100 == 0:            # print(f'batch index: batch_idx, loss: loss.item()')  # item()方法将单个tensor转化成数字            print(f'[ batch_idx + 1 :>5d / batch_num :>5d ] loss: loss.item()')    # 统计一个周期的平均loss    avg_loss = epoch_loss / batch_num    avg_accuracy = correct / size    return  avg_accuracy, avg_loss # 验证and评估 def test_and_val(dataloader, net, loss_fn):    size = len(dataloader.dataset)    batch_num = len(dataloader)    correct = 0    losses = 0    net.eval()    with torch.no_grad():        for x, y in dataloader:            x, y = x.to(device), y.to(device)            pred = net(x)            loss = loss_fn(pred, y)            losses += loss.item()            correct += (pred.argmax(1) == y).type(torch.int).sum().item()    accuracy = correct / size    avg_loss = losses / batch_num    # print(f'The Accuracy = accuracy * 100%')    return accuracy, avg_loss if __name__ == '__main__':    transform = transforms.Compose([        transforms.ToTensor(),        transforms.Normalize(0.1307, 0.3081)])    # (0) 测试机器是否支持GPU    data_train_acc = []    data_train_loss = []    data_val_acc = []    data_val_loss = []    device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")    # batch_size = [32,64,128,256]    batch_size = [64]    train_all_ds = torchvision.datasets.MNIST(root="data", download=True, train=True, transform=transform, )    # 将训练集划分为训练集+验证集    train_ds, val_ds = torch.utils.data.random_split(train_all_ds, [50000,10000])    test_ds = torchvision.datasets.MNIST(root="data", download=True, train=False, transform=transform, )    for each in range(len(batch_size)):        train_loader = DataLoader(dataset=train_ds,batch_size=batch_size[each], shuffle=True,)        val_loader = DataLoader(dataset=val_ds,batch_size=batch_size[each],)        test_loader = DataLoader(dataset=test_ds,batch_size=batch_size[each],)        # (5) 网络的输入、输出以及测试网络的性能(不经过任何训练的网络)        net = MyNet().to(device)        optimizer = torch.optim.SGD(net.parameters(), lr=0.01)        loss_fn = torch.nn.CrossEntropyLoss()        # （6）训练周期        begin_time = time()        train_accuracy_list = []        train_loss_list = []        val_accuracy_list = []        val_loss_list = []        epoch = 10        for t in range(epoch):            print(f"Epoch t + 1")            train_accuracy, train_loss = train(train_loader, net, loss_fn, optimizer)            train_accuracy_list.append(train_accuracy)            train_loss_list.append(train_loss)            print(f'Epoch t + 1 :<2d Train Acc = train_accuracy * 100 :.2f%  ||  Epoch t + 1 Train Loss = train_loss')            val_accuracy, val_loss = test_and_val(val_loader, net, loss_fn)            val_accuracy_list.append(val_accuracy)            val_loss_list.append(val_loss)            print(f'Epoch t + 1 :<2d Val Acc   = val_accuracy * 100 :.2f%  ||  Epoch t + 1 Val Loss   = val_loss')        # print(f'Best_Train_Acc = max(train_accuracy_list) * 100%  ||  Best_Val_Acc = max(val_accuracy_list) * 100%')        data_train_acc.append(train_accuracy_list)        data_train_loss.append(train_loss_list)        data_val_acc.append(val_accuracy_list)        data_val_loss.append(val_loss_list)    data_set = [data_train_acc,data_train_loss,data_val_acc,data_val_loss]    file = xlwt.Workbook('encoding = utf-8')  # 设置工作簿编码    sheet1 = file.add_sheet('数据', cell_overwrite_ok=True)  # 创建sheet工作表    # 要写入的列表的值    name = ['train_acc_batch','train_loss_batch','val_acc_batch','val_loss_batch']    # for one in range(len(data_set)):    #     data = data_set[one]    #     id = name[one]    #     for i in range(len(data)):    #         for j in range(len(data[i])):    #             sheet1.write(j, i, data[i][j])  # 写入数据参数对应 行, 列, 值    #     file.save(f'CNN1_CH_id.xls')  # 保存.xls到当前工作目录    print(f'Best_Train_Acc = max(train_accuracy_list) * 100 :.2f%, Best_Val_Acc = max(val_accuracy_list) * 100 :.2f%')    test_accuracy,_ = test_and_val(test_loader, net, loss_fn)    print(f'Test Acc = test_accuracy * 100%')    end_time = time()    print('Time Consumed:',end_time-begin_time)

卷积降维与池化降维对精度的影响

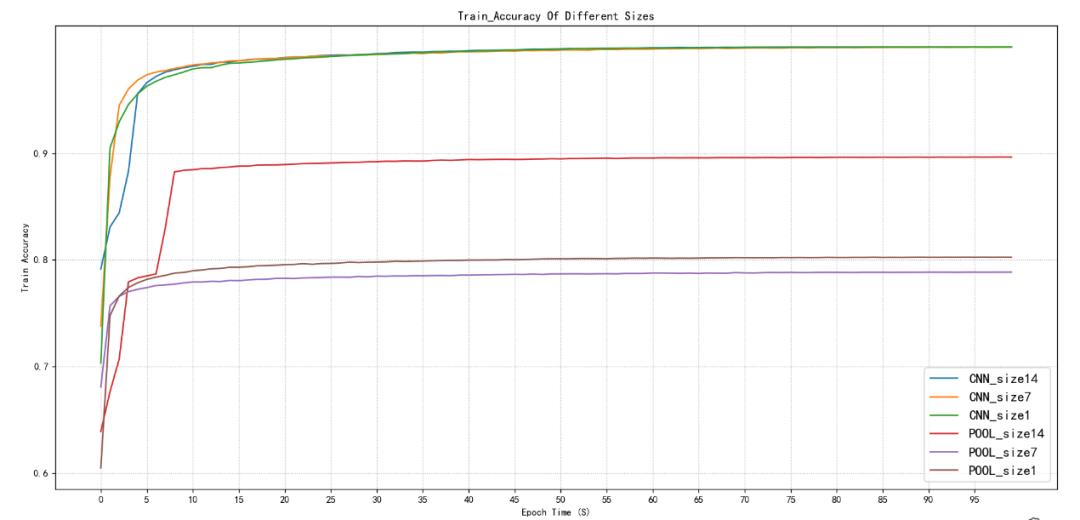
图2.1训练集精度对比

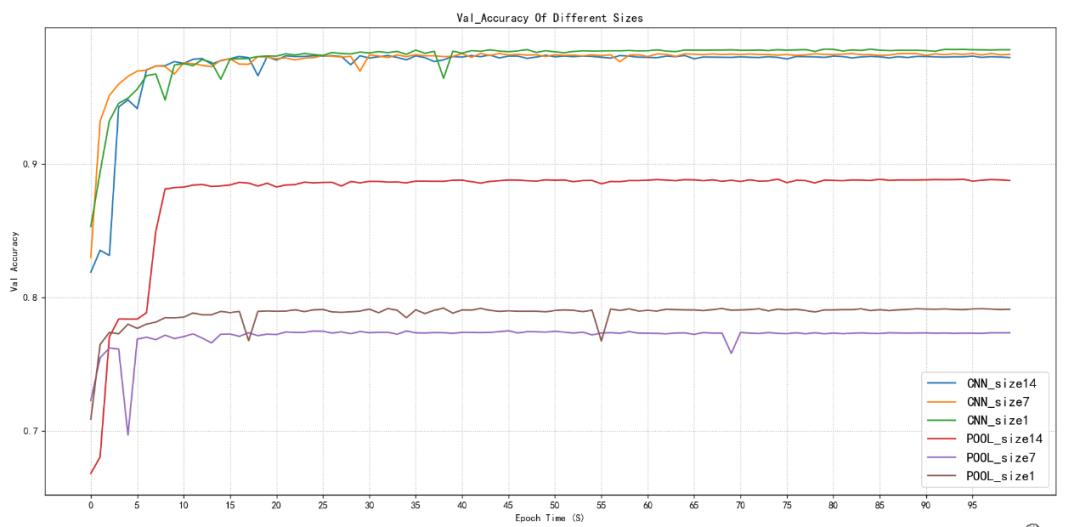
图2.2验证集精度对比

如图2.1和图2.2所示在使用卷积降维的情况下无论特征图尺寸在14x14、7x7、1x1在训练集下，精度最开始都是从80%多在10个周期以后均能达到99%左右，最终预测精度能达到99.99%，并且在10个周期以后就达到99%，再训练90个周期就是缓慢的从99%到99.99%几乎接近1的精度了。训练集也是如此，10个周期左右达到98%，最后稳定在98.40%左右。

池化降维，无论训练集还是验证集在14x14、7x7，1x1在首次只有60%多的准确率，在14x14的尺寸下，池化降维可以接近90%的准确率，大致在88%-89%，7x7、1x1均只能达到78%-79%左右，并且都是在10个周期左右趋于稳定，只有小幅波动。

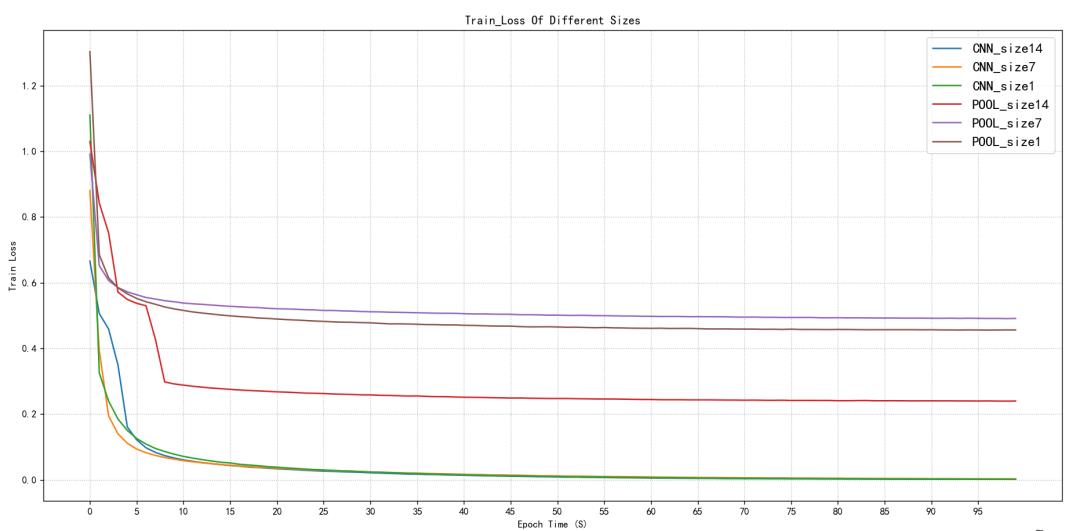
图2.3训练集损失值对比

卷积降维与池化降维对损失值的影响

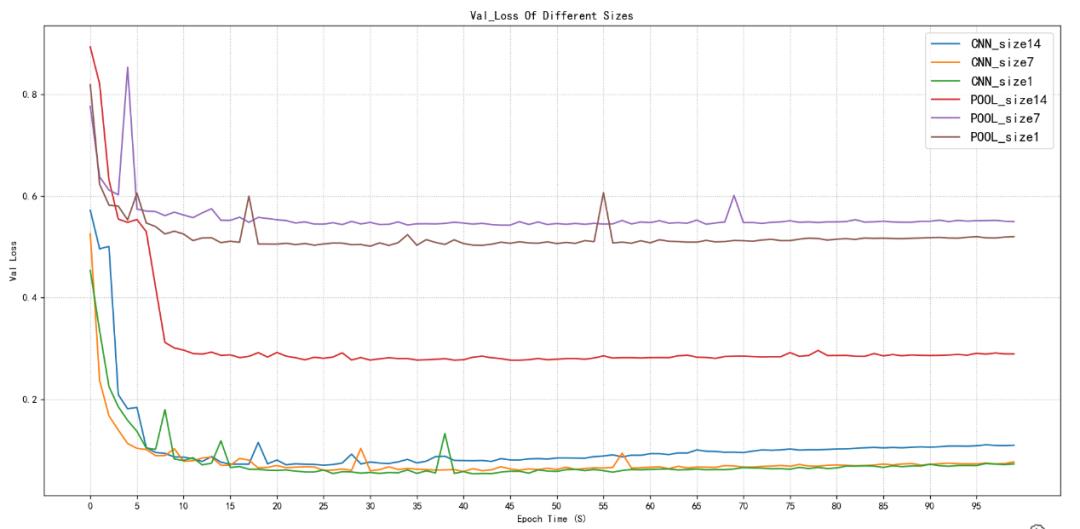
图2.4验证集损失值对比

如图2.3和2.4所示，卷积降维训练集与验证集的损失值在首次就能达到池化降维的最小值，并且卷积降维随着训练次数的增加还在持续减小，几乎能够达到0.00几的损失值，最后稳定在这附近波动，代表预测值与真实值之间的差距非常小，几乎接近。

然后池化降维首次就是0.8-0.9左右，随着训练次数增加最低值也就只有0.5-0.6左右。但是池化降维在14x14尺寸下其损失值可以相对于在池化降维下7x7、1x1的尺寸下较小一些，可以达到0.3左右的损失值。

3 结语

针对卷积降维和池化降维，这里是对特征图14x14、7x7、1x1进行了精度对比和损失值对比的分析，最终得出在对于降维的方法使用下，卷积降维效果更佳，但需要人为去计算出该卷积出来的特征图大小，但是池化可以直接很简单的得出特征图大小，这是其中一个区别，也是池化特征的一个优点。但是对于实验结果的效果，卷积降维要更好与池化降维的。能够使训练集精度达到99.99%，验证集精度达到98.40%左右。这是卷积降维的优点所在。

在本次实验中，得出的最后的结论是，卷积降维对于结果精度要优于池化降维，但是卷积降维需要人为来计算卷积后的特征图大小，从而去更改卷积层的参数，有时候较为麻烦。池化降维则可以轻易的得出想要的特征图大小。

对于本次实验只是比较了特征图14x14、7x7、1x1，这三个尺寸对于精度的影响不同。还可以试着比较训练花费时间。以及不同尺寸是否对结果有什么影响。这次实验数据也有不同尺寸的结果，我也同时对比了一下在卷积层最后不同的尺寸对于精度的影响，最后发现只有前10个周期有一点区别，最终均能达到最优的效果，但是为了计算量的减少，在同等结果的情况下，尺寸小那么更节省时间吧。