机器学习模型评价指标及拟合概念

Posted 2023-03-03 ironyl

机器学习模型评价指标及拟合概念

• • 一、机器学习模型评价指标
  • • 回归问题等连续值的差值的判断
    • • • 1） MAE平均绝对误差：
        • 2）MSE均方误差：
        • 3）RMSE均方根误差：
        • 4）R平方：
    • 分类问题
    • • • 1）混淆矩阵
        • 2）准确度（Accuracy）
        • 3）精度或查准率（Precision）
        • 4) 召回率（Recall）
        • 5）调和平均（F1（本质上相当于β取1） Score）
        • 6）F-β Score
  • 二、拟合概念
  • • • • 1、欠拟合（Underfitting）
        • 2、过拟合（Overfitting）

一、机器学习模型评价指标

回归问题等连续值的差值的判断

回归问题常用的基本性能度量基本都是基于预测值与真实值之间的误差来作为评价验证标准的，如下常用的有：

1） MAE平均绝对误差：

$$MAE=\frac{1}{n}\sum _{i=1}^n|f_i-y_i|$$

2）MSE均方误差：

$$MAE=\frac{1}{n}\sum _{i=1}^n(f_i-y_i{)}^2$$

3）RMSE均方根误差：

$$RMSE=\sqrt{MSE}$$

4）R平方：

$$r^2=1-\frac{S{S}_{res}}{S{S}_{tot}}=1-\frac{\sum (y_i-f_i{)}^2}{\sum (y_i-\bar{y}{)}^2}$$

分类问题

以二分类问题为例，尝试用以下几种方法进行评估：

1）混淆矩阵

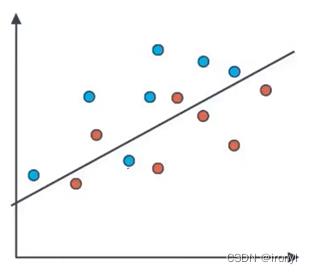
假设蓝色的点是正点，红色是负点，可根据得出模型规则划分出点的阵营，以上图为例：

	Guessed positive	Guessed negative
Positive	True Positives = 6	False Negative = 1
Negative	False Positive = 2	True Negative = 5

因此得到该二分类的混淆矩阵为：$\left[\begin{array}{cc}6& 1\\ 2& 5\end{array}\right]$
缺陷：虽然包含全部的信息，但对结果展示并不直观，为了更直观的显示一个模型的好坏，可能仍需要使用额外的指标去度量模型的好坏

2）准确度（Accuracy）

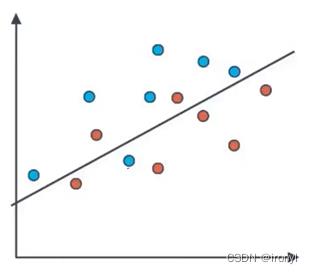
准确度本质上来说就是计算模型分类以后，正确分类的点有多少个，也就是分类正确的点占全部样本的比例。
仍以上述为例：蓝色点表示positive，红色点表示negative
$$accuracy=\frac{6+5}{14}=78.6\%$$
缺陷：准确度会有一些信息的损失，且并不适用于所有的场景，比如检测某人是否患有罕见病，显然患有罕见病的几率是比较低的，监测正常的病人数准确度确实很高，但不能达到检测罕见病的目的（样本分布极度不平衡等情况）,会存在一定的局限性

3）精度或查准率（Precision）

使用获取的混淆矩阵为基础去进行精度的计算，以上述获取的矩阵为例：
当前混淆矩阵为：$$\left[\begin{array}{cc}6& 1\\ 2& 5\end{array}\right]$$
当前被猜测为posiive点的总共有8(2+6)个，其中有6个是预测正确的positive，那么我们所求取的精度为：
$$Precision=\frac{6}{2+6}=75\%$$
精度越高，说明预测的的准确率越高，模型越好

4) 召回率（Recall）

能够考察当前模型究竟检测出多少的正确有效值，仍然以上述混淆矩阵为例，positive的训练样本点共7(6+1)个，其中6个被检测出来为positive，则召回率为：
$$Recall=\frac{6}{6+1}=85.7\%$$
例子：检测垃圾邮件，现有280000封非垃圾邮件，有566封垃圾邮件，分别计算当将所有邮件检测为垃圾邮件的精度和召回率，当所有邮件检测为非垃圾邮件的精度和召回率。
全部诊断为垃圾邮件：

	Guessed-SPAM	Guessed-Non-SPAM
SPAM	566	0
Non-SPAM	280000	0

$$Precision=\frac{566}{566+280000}，Recall=\frac{566}{566}$$
全部诊断为非垃圾邮件：

	Guessed-SPAM	Guessed-Non-SPAM
SPAM	0	566
Non-SPAM	0	280000

$$Precision=\frac{0}{0}，Recall=\frac{0}{566}$$

5）调和平均（F1（本质上相当于β取1） Score）

当调和平均比较大的时候就能够说明你的模型的处理数据达到目的程度是不错的，分析如下：

以上述为例，平均调和相当于将精度和召回率平均了一下，精度相当于True Positive+False Positive ，召回率相当于True Positive+False Positive，当平均调和比较高的时候，精度中的False Positive和召回率中的False Negative都是比较低的，那么相对来说分类形成的正确数目就会越多，因此能够对模型进行良好的评价(未采用两个相加/2的方式实现平均，是为了只要精度或者召回率有一方逼近0，那么调和平均就逼近0)。
调和平均计算如下：
$$F1Score=2\ast \frac{Precision\ast Recall}{Precision+Recall}$$

6）F-β Score

F1 Score中精度和召回率所占的比例是均衡的，也就是五五开，但有时候我们的模型希望精度或者召回率二者之一所占的权重更大，就衍生出了F-β Score,当β=1时，其实就是F1 Score。
计算如下：
$$F_{\beta }=(1+{\beta }^2)\ast \frac{precision\ast recall}{({\beta }^2\ast precision)+recall}$$
由上式观察可知，当β>1时，recall所占的权重是更大的，当β<1时，precision所占的权重是更大的，因此通过β能调节而这所占的比例，权重占比选择可以根据实际问题选择。
比如以下question：
①检测飞机的故障零件
解释：对于precision而言，表示检测出的故障零件中真实故障零件的占比；对于recall而言，表示真实故障零件中测出的故障零件数目占比；显然关于检测故障零件我们需要确定检测出的故障零件数目，对于现实故障零件数目越少越好，因此β>1能够增大recall在计算中所占的权重
②向潜在的客户寄送免费的样品
解释：样本需要成本，如果赠送后能够返回购买产品的我们理解为潜在客户，就precision而言表示检测出的潜在客户中真实潜在客户的占比；而recall是真实的潜在客户中我们测出来的潜在客户的占比；显而易见，真实的潜在顾客检测出来占比越高越值得赠送样品来拉拢客户，因此β<1能增大precision在计算中所占的权重
③向手机中发送关于用户可能喜欢的视频的通知
解释：关于推送视频通知，更偏向于precision或者recall并没有对更显著的效果，所以而这权重基本五五开，用调和平均计算即可，即β=1

注：多分类问题与二分类问题获取混淆矩阵和计算准确度不尽相同，只是在计算precisin和recall的时候需要指定一下正例（positive）
以mnist手写识别为例，假设以下为识别数据后获取到的混淆矩阵：

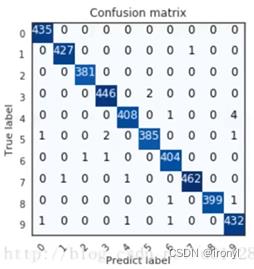
假设指定“7”作为模型的正例，那么 p r e c i s i o n = 432 432 + 1 + 1 + 4 （第 10 列）