多维时序 | MATLAB实现GTO-CNN-GRU人工大猩猩部队优化卷积门控循环单元多变量多步时间序列预测

Posted 2023-03-02 机器学习之心

多维时序 | MATLAB实现GTO-CNN-GRU人工大猩猩部队优化卷积门控循环单元多变量多步时间序列预测

目录

• • 多维时序 | MATLAB实现GTO-CNN-GRU人工大猩猩部队优化卷积门控循环单元多变量多步时间序列预测
  • • 预测效果
    • 基本介绍
    • 模型描述
    • 程序设计
    • 学习总结
    • 参考资料

预测效果

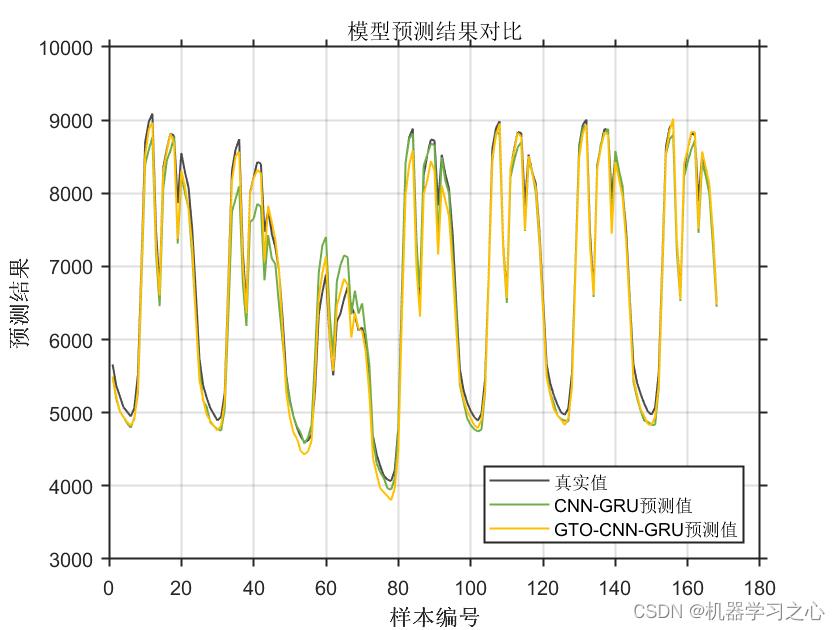
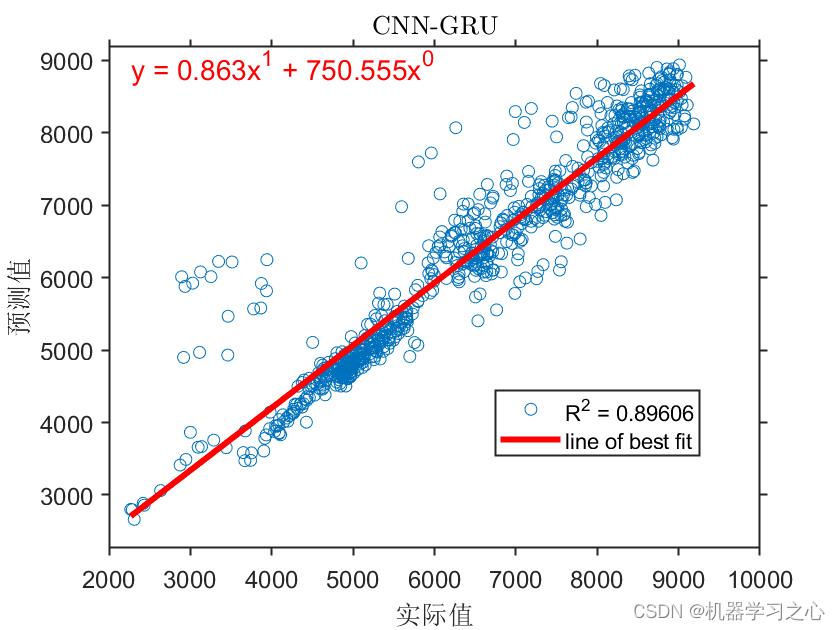
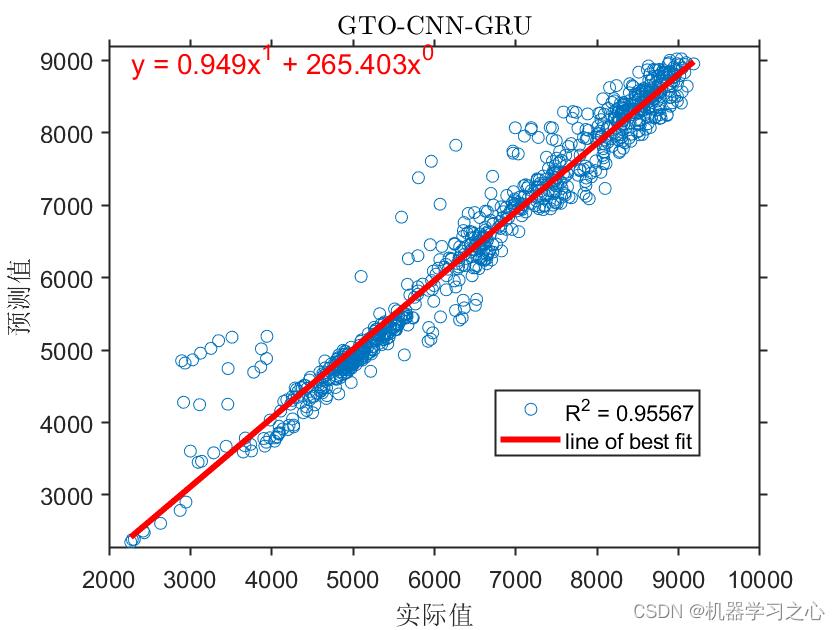
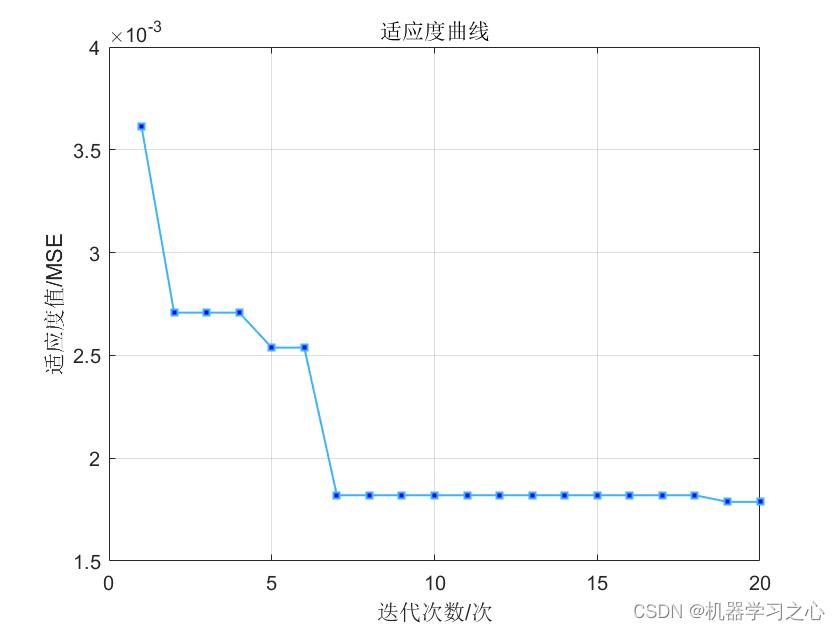
基本介绍

MATLAB实现GTO-CNN-GRU人工大猩猩部队优化卷积门控循环单元多变量多步时间序列预测。提出了一种基于GTO-CNN-GRU（convolutional neural networks-gate recurrent unit）神经网络的电力系统短期负荷预测方法。 结果表明：与单独的CNN -GRU 网络相比，GTO-CNN-GRU 网络对电力系统短期负荷的预测误差更小，预测精度更高。

模型描述

GTO优化CNN-GRU，分为GTO部分、CNN-GRU部分和数据部分。首先根据 GTO传入的参数进行解码，获得所需超参数，然后利用数据部分传入的训练集进行网络训练，获得实际输出值与期望输出值的误差均方差，并将均方差作为适应度值返回给GTO部分。GTO部分根据适应度值进行优化，实现种群与全局最优解的更新。 通过该方法，最终可获得优化的网络超参数。进而使用卷积神经网络（CNN）对负荷及气象数据进行卷积处理，以更好地提取数据新特征，增强输入数据与输出数据间的相关性。然后使用门控循环单元（GRU）实现短期负荷预测。使用某地区的负荷数据结合当地的气象数据，对CNN-GRU方法进行了测试。

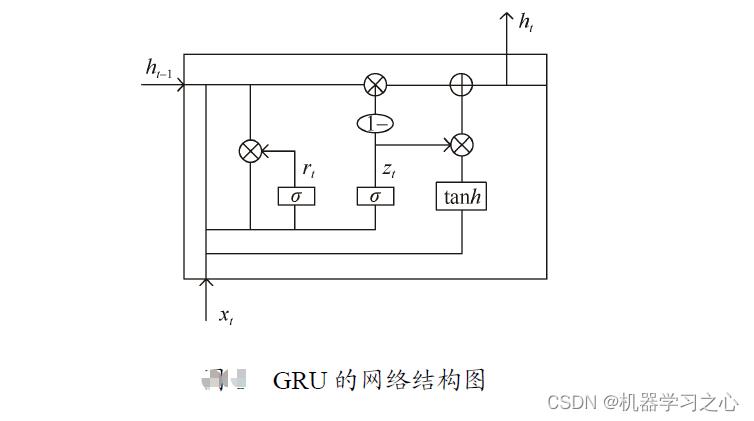
将经过卷积之后产生的特征序列作为GRU的输入。GRU 由LSTM 发展而来，LSTM 是RNN的变体。RNN 网络通过对输入信号的循环保证了信号的持续存在。LSTM 是由RNN 网络改进而来，在RNN 的基础上加入了记忆单元和门机制，有效地解决了长序列训练中存在的梯度消失和梯度爆炸问题。LSTM 用输入门、遗忘门和输出门3 个门函数来控制输入值、遗忘值和输出值。GRU 网络较LSTM 网络有所简化，GRU 网络由新门和重置门两个门函数构成。

程序设计

• 完整源码和数据私信博主获取或同等价值程序兑换获取。

function [lb,ub,dim,fobj] = Get_Functions_details(F)




% F1

function o = F1(x)
o=sum(x.^2);
end

% F2

function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end

% F3

function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
    o=o+sum(x(1:i))^2;
end
end

% F4

function o = F4(x)
o=max(abs(x));
end

% F5

function o = F5(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end

% F6

function o = F6(x)
o=sum(abs((x+.5)).^2);
end

% F7

function o = F7(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end

% F8

function o = F8(x)
o=sum(-x.*sin(sqrt(abs(x))));
end

% F9

function o = F9(x)
dim=size(x,2);
o=sum(x.^2-10*cos(2*pi.*x))+10*dim;
end

% F10

function o = F10(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end

% F11

function o = F11(x)
dim=size(x,2);
o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;
end

% F12

function o = F12(x)
dim=size(x,2);
o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));
end

% F13

function o = F13(x)
dim=size(x,2);
o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...
((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));
end

% F14

function o = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];

for j=1:25
    bS(j)=sum((x'-aS(:,j)).^6);
end
o=(1/500+sum(1./([1:25]+bS))).^(-1);
end

% F15

function o = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end

% F16

function o = F16(x)
o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end

% F17

function o = F17(x)
o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end

% F18

function o = F18(x)
o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
    (30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end

% F19

function o = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
o=0;
for i=1:4
    o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end

% F20

function o = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
o=0;
for i=1:4
    o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end

% F21

function o = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

o=0;
for i=1:5
    o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

% F22

function o = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];

o=0;
for i=1:7
    o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end

% F23

function o = F23(x<
以上是关于多维时序 | MATLAB实现GTO-CNN-GRU人工大猩猩部队优化卷积门控循环单元多变量多步时间序列预测的主要内容，如果未能解决你的问题，请参考以下文章
 
 Keras LSTM实现多维输入输出时序预测实践详解
 时序预测 | MATLAB实现LSTM-SVR(长短期记忆神经网络-支持向量机)时间序列预测
 多维尺度分析（Multidimensional scaling）与MATLAB实现
 怎样用matlab实现多维K-means聚类算法
 解读顶会ICDE’21论文：利用DAEMON算法解决多维时序异常检测问题
 基于matlab智能优化与机器学习结合算法数据预测清单