[算法读书笔记]二分查找算法

Posted 2023-02-15 凌星An

二分查找算法

百度百科:
二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。
它充分利用了元素间的次序关系，采用分治策略，可在最坏的情况下用O(log n)完成搜索任务。
它的基本思想是：（这里假设数组元素呈升序排列）
将n个元素分成个数大致相同的两半，取a[n/2]与欲查找的x作比较，
如果x=a[n/2]则找到x，算法终止；
如果x<a[n/2]，则我们只要在数组a的左半部继续搜索x；
如果x>a[n/2]，则我们只要在数组a的右半部继续搜索x。

图解:
比如，下面是一个有序的序列，我们要查找4这个值，使用二分是怎么进行的呢

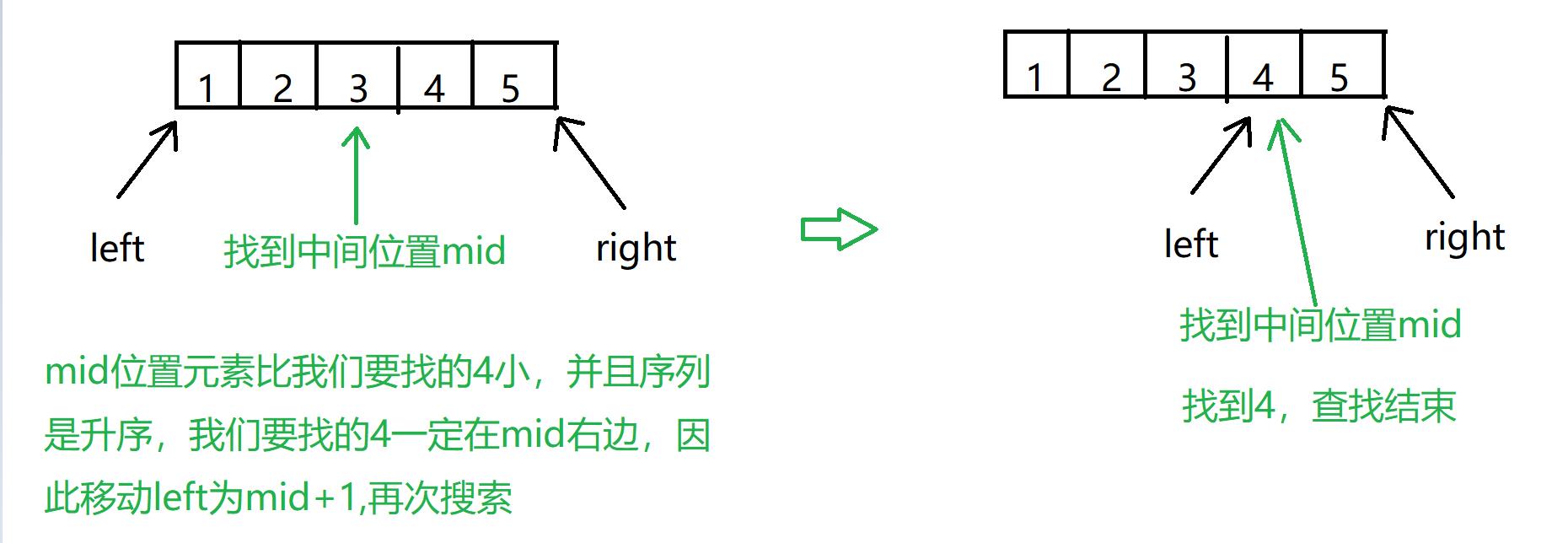
题目练习

704. 二分查找
     链接：https://leetcode-cn.com/problems/binary-search/
     

int search(int* nums, int numsSize, int target)
        //左右边界
        int left=0,right=numsSize-1;
        while(left<=right)
            //计算中间节点
            int mid=left+right>>1;
            if(nums[mid]==target)
               //等于查找值，返回
                return mid;
            else if(nums[mid]>target)
           //中间节点的值，比我们要查找的值大，则要查找的值在中间节点左边
           //移动右边界
                right=mid-1;
            else
          //中间节点的值，比我们要查找的值小，则要查找的值在中间节点右边
          //移动左边界
                left=mid+1;
            
        
        return -1;

代码实现

我们要查找的区间为[left,right]    左，右边界也在区间内

1.
check()函数为真，结果在左区间及中点
即将区间划分为[left,mid] 和[mid+1,right]
while(left<right)
     int mid=left+right>>1;
     if( check() )
          right=mid;
     else
          left=mid+1;
     

//这种算法，是寻找区间[left,right]中最左边为target的算法
2.
check()函数为真，结果在右区间及中点
即将区间划分为[left,mid-1] 和[mid,right]
while(left<right)
     int mid=left+right+1>>1;
     if( check() )
          left=mid;
     else
          right=mid-1;
     

//这种算法，是寻找区间[left,right]中最右边为target的算法

还是上面的题目，我们使用刚刚的二分查找算法进行改写
704. 二分查找
链接：https://leetcode-cn.com/problems/binary-search/

int search(int* nums, int numsSize, int target)
        int left=0,right=numsSize-1;
        while(left<right)
            int mid=left+right>>1;
            if(nums[mid] >=target)
                 //倘若中间值比target要小，则target一定在mid的右边，
                //可划分为[left,mid] [mid+1 ,right]
                right=mid;
            else
                left=mid+1;
            
        
        return nums[left]==target?left:-1;

int search(int* nums, int numsSize, int target)
        int left=0,right=numsSize-1;
        while(left<right)
            int mid=left+right+1>>1;
            if(nums[mid] <=target)
               //倘若中间值比target要大，则target一定在mid的左边，
                //可划分为[left,mid-1] [mid ,right]
                left=mid;
            else
                right=mid-1;
            
        
        return nums[left]==target?left:-1;

浮点数二分查找

这个很少情况下，会使用，不做详细解释，如向详细了解，可前往参考页面.

while(right-left <1e-6)
       double mid= (left+right)/2;
       if(check() )
           left=mid;
       else
           right=mid;
       

参考：
https://www.acwing.com/blog/content/277/