0042. Trapping Rain Water (H)

Posted 2020-12-13 墨云黑

Trapping Rain Water (H)

题目

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

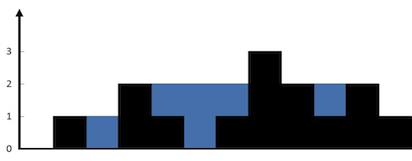
The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!

Example:

Input: [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
Output: 6

---

题意

计算由给定数组构成的高度图能够存储的最大水量(图中蓝色区域)。

思路

暴力法：对于每一个下标位置，当前位置高度为cur，找到它左侧的最大高度leftMax，及右侧的最大高度rightMax，如果两者都大于cur，说明在当前位置可以存水，可存水量为min(leftMax, rightMax) - cur。复杂度为\\(O(N^2)\\)。(一开始想到的暴力法是奇葩的从下往上扫描找空格hhh)

动态规划优化的暴力法：暴力法效率较低的原因在于每一次都要重新计算左右两侧的最大高度，通过动态规划提前将每个位置左右两侧的最大高度记录下来可以大大提高效率。复杂度为\\(O(N)\\)。
记dp[i]为以i为端点的左/右区间中的最大高度，那么有 \\(dp[i]=max(dp[i-1],\\ height[i])\\)。

官方解答还提供了压栈法和Two pointers解法。

压栈法：从左到右遍历数组，若栈空或当前下标cur对应高度小于栈顶下标top对应高度，则将cur压入栈，这保证了栈中每一个下标的高度是递减的；若 height[cur] > height[top]，同时top的高度又小于栈中前一个下标对应的高度，说明在下标top处可以存水(左右两边高度大于height[top])，将top出栈并计算存储的水量，重复上述过程直到cur对应高度不大于此时栈顶下标高度，将cur压入栈。

Two Pointers：左右两边各设一个指针left和right向中间移动，每次判断，如果 height[left] < height[right]，且 height[left] < leftMax，说明left位置被leftMax和height[right]包围，可以存水，若 height[left] > leftMax，则更新leftMax；如果 height[right] <= height[left]，且 height[right] < rightMax，说明right位置被rightMax和height[left]包围，可以存水，若 height[right] < rightMax，则更新rightMax。

---

代码实现

Java

动态规划优化

class Solution {
    public int trap(int[] height) {
        if (height.length == 0) {
            return 0;
        }
        
        int sum = 0;
        int[] leftMaxHeight = new int[height.length];
        int[] rightMaxHeight = new int[height.length];
        
        // 动态规划记录左右最大高度信息
        leftMaxHeight[0] = height[0];
        rightMaxHeight[height.length - 1] = height[height.length - 1];
        for (int i = 1; i < height.length - 1; i++) {
            int j = height.length - i - 1;
            leftMaxHeight[i] = Math.max(leftMaxHeight[i - 1], height[i]);
            rightMaxHeight[j] = Math.max(rightMaxHeight[j + 1], height[j]);
        }
        
        for (int i = 0; i < height.length; i++) {
            int leftMax = leftMaxHeight[i];
            int rightMax = rightMaxHeight[i];
            if (leftMax > height[i] && rightMax > height[i]) {
                sum += Math.min(leftMax, rightMax) - height[i];
            }
        }

        return sum;
    }
}

压栈法

class Solution {
    public int trap(int[] height) {
        int sum = 0, cur = 0;
        Deque<Integer> stack = new ArrayDeque<>();

        while (cur < height.length) {
            while (!stack.isEmpty() && height[cur] > height[stack.peek()]) {
                int top = stack.pop();
                if (stack.isEmpty()) {
                    break;
                }
                int dx = cur - stack.peek() - 1;
                int dy = Math.min(height[cur], height[stack.peek()]) - height[top];
                sum += dx * dy;
            }
            stack.push(cur++);
        }
        
        return sum;
    }
}

Two Pointers

class Solution {
    public int trap(int[] height) {
        int sum = 0;
        int left = 0, right = height.length - 1;
        int leftMax = -1, rightMax = -1;

        while (left < right) {
            if (height[left] < height[right]) {
                if (height[left] > leftMax) {
                    leftMax = height[left];
                } else {
                    sum += leftMax - height[left];
                }
                left++;
            } else {
                if (height[right] > rightMax) {
                    rightMax = height[right];
                } else {
                    sum += rightMax - height[right];
                }
                right--;
            }
        }

        return sum;
    }
}

javascript

动态规划优化

/**
 * @param {number[]} height
 * @return {number}
 */
var trap = function (height) {
  let len = height.length
  let left = new Array(len).fill(0)
  let right = new Array(len).fill(0)

  for (let i = 1; i < len; i++) {
    left[i] = Math.max(left[i - 1], height[i - 1])
    right[len - 1 - i] = Math.max(right[len - i], height[len - i])
  }

  let sum = 0
  for (let i = 1; i < len - 1; i++) {
    if (left[i] > height[i] && right[i] > height[i]) {
      sum += Math.min(left[i], right[i]) - height[i]
    }
  }

  return sum
}

压栈法

/**
 * @param {number[]} height
 * @return {number}
 */
var trap = function (height) {
  let sum = 0
  let stack = []

  for (let i = 0; i < height.length; i++) {
    while (stack.length > 0 && height[i] > height[stack[stack.length - 1]]) {
      let j = stack.pop()
      if (stack.length === 0) {
        break
      }
      let k = stack[stack.length - 1]
      let dx = i - k - 1
      let dy = Math.min(height[i], height[k]) - height[j]
      sum += dx * dy
    }
    stack.push(i)
  }

  return sum
}

Two Pointers

/**
 * @param {number[]} height
 * @return {number}
 */
var trap = function (height) {
  let sum = 0
  let left = 0, right = height.length - 1
  let leftMax = -1, rightMax = -1

  while (left < right) {
    if (height[left] < height[right]) {
      if (height[left] > leftMax) {
        leftMax = height[left++]
      } else {
        sum += leftMax - height[left++]
      }
    } else {
      if (height[right] > rightMax) {
        rightMax = height[right--]
      } else {
        sum += rightMax - height[right--]
      }
    }
  }

  return sum
}