PPOJ刷题-3

Posted 2023-03-01 Mr.wu123

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了PPOJ刷题-3相关的知识，希望对你有一定的参考价值。

PPOJ刷题-3

1265: 最近公共祖先

题目描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

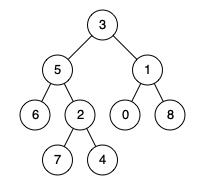
输入

输入两行。
第一行按照先序输入一棵二叉树，其中空节点用 -1 表示。
第二行输入两个结点的值val1, val2 , 输出该结点的双亲节点的val.(数据保证所有节点val的值都不相同)

输出

输出一行，代表最近公共祖先的val。

样例输入

3 5 6 -1 -1 2 7 -1 -1 4 -1 -1 1 0 -1 -1 8 -1 -1
5 1

样例输出

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//先序遍历建立二叉树，然后对其进行先序遍历，
//如果某个结点的左子树和右子树都找到了权值为a和b的结点，则该节点就是最近公共结点
struct TreeNode 
   int val;
   TreeNode *left,*right;
;


void build(TreeNode * &T)

    int x;
    cin>>x;
    if(x==-1)
        T==NULL;
        return ;
    
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);


TreeNode *Find(TreeNode *T,int a,int b)

    //如果该节点权值为a或b，或者该节点为空，返回该结点
    if(T==NULL||T->val==a||T->val==b) return T;
    //递归查找左子树和右子树，将结果分别保存在l和r
    TreeNode *l=Find(T->left,a,b),*r=Find(T->right,a,b);
    //如果在左右子树找到了，就返回该节点
    if(l && r) return T;
    //否则说明在同一子树上；对于一个结点是另一个结点祖先的情况，先找到的结点就是最近公共祖先
    else return l?l:r;


int main()

    TreeNode * T=NULL;
    build(T);
    int a,b;
    cin>>a>>b;
    cout<<Find(T,a,b)->val<<endl;
    return 0;

1266: 二叉树的直径

题目描述

二叉树的直径是指二叉树中相距最远的两个点的距离。如下图所示二叉树，最远的两个点是7和13或者 4和13，故二叉树直径为6.

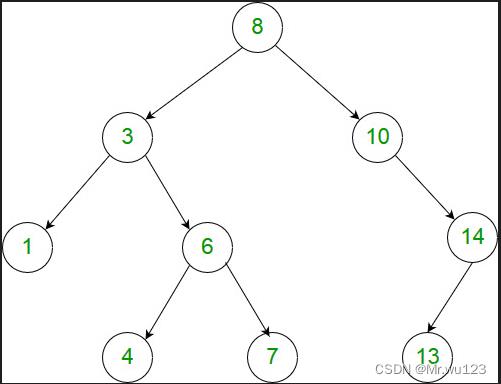
输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

输出一行代表二叉树的直径。

样例输入

8 3 1 -1 -1 6 4 -1 -1 7 -1 -1 10 -1 14 13 -1 -1 -1

样例输出

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//先序遍历建立二叉树，求二叉树中相距最远的两个点的距离
//只需要每个结点的的左子树的最大深度+右子树的最大深度
struct TreeNode 
   int val;
   TreeNode *left,*right;
;
int MaxL=0;

void build(TreeNode * &T)

    int x;
    cin>>x;
    if(x==-1)
        T==NULL;
        return ;
    
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);


//求解以该节点为根节点的最大深度
int Depth(TreeNode *T,int h)

    //若该结点为空，就返回深度
    if(T==NULL) return h;
    //分别求出左右子树的深度
    int l=Depth(T->left,h+1),r=Depth(T->right,h+1);
    return max(l,r);


//寻找二叉树中相距最远的两个点的距离
void Find(TreeNode *T)

    if(T==NULL) return;
    int l,r;
    //左子树不为空则求左子树的深度，为空则深度为0
    l=T->left?Depth(T->left,0):0;
    //右子树不为空则求右子树的深度，为空则深度为0
    r=T->right?Depth(T->right,0):0;
    if(MaxL<l+r) MaxL=l+r;
    Find(T->left);
    Find(T->right);


int main()

    TreeNode * T=NULL;
    build(T);
    MaxL=0;
    Find(T);
    cout<<MaxL<<endl;
    return 0;

1364: 删除给定值的叶子节点

题目描述

PIPI有一棵二叉树和一个整数 target ，请你删除所有值为 target 的叶子节点。
注意，一旦删除值为 target 的叶子节点，它的父节点就可能变成叶子节点；如果新叶子节点的值恰好也是 target ，那么这个节点也应该被删除。

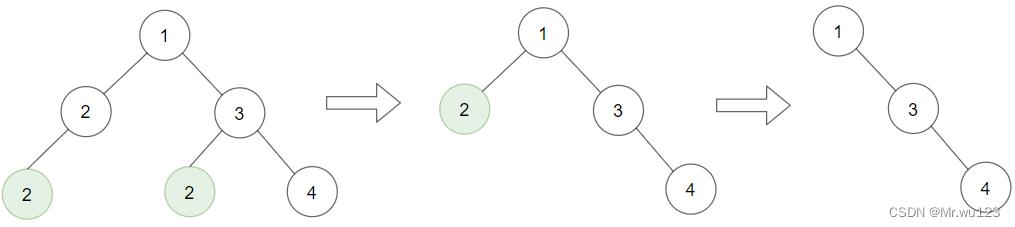
输入

第一行按照先序输入树T，其中空节点用 -1 表示。
第二行输入target

输出

按照先序输出删完之后的二叉树。

样例输入

1 2 2 -1 -1 -1 3 2 -1 -1 4 -1 -1
2

样例输出

1 3 4

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//采用后序遍历进行查找，因为要先知道子节点被删除没有；
//记录每一个结点的父亲结点，以及当前结点是父节点的左孩子还是右孩子（0左1右）
//如果当前结点值为target并且左右子树都为空，那就将父节点的左（右）孩子置空
struct TreeNode 
   int val;
   TreeNode *left,*right;
;

void build(TreeNode * &T)

    int x;
    cin>>x;
    if(x==-1)
        T==NULL;
        return ;
    
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);


void Delete(TreeNode *root,TreeNode *fa,int son,int target)//son=0左孩子，son=1右孩子

    if(!root) return;
    Delete(root->left,root,0,target);
    Delete(root->right,root,1,target);
    //如果结点值为target，且左右子树为空就删除
    if(root->val==target && root->left==NULL && root->right==NULL)
        if(son==0) fa->left=NULL;
        else fa->right=NULL;
    


void Print(TreeNode *T)//先序输出

    if(T==NULL) return;
    printf("%d ",T->val);
    Print(T->left);
    Print(T->right);


int main()

    TreeNode * T=NULL;
    build(T);
    int target;
    cin>>target;
    Delete(T,T,-1,target);
    //根节点为target
    if(T->val==target && T->left==NULL &&T->right==NULL)
        T=NULL;
    Print(T);
    return 0;

1365: 祖父结点为偶数的节点

题目描述

PIPI有一棵二叉树，他想知道所有祖父结点值为偶数的结点值之和。

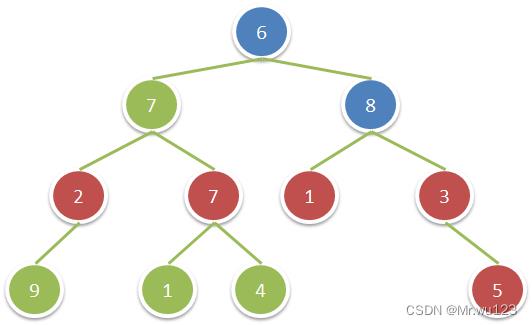
输入

输入包含一行，先序输入一棵二叉树，空节点用-1表示。

输出

输出为满足条件的结点值之和。

样例输入

6 7 2 9 -1 -1 -1 7 1 -1 -1 4 -1 -1 8 1 -1 -1 3 -1 5 -1 -1

样例输出(2+7+1+3+5=18)

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//每次遍历保存该节点的父节点和祖父结点，判断祖父结点是否为偶数即可
//递归时，当前结点变父节点，父节点变祖父结点
struct TreeNode 
   int val;
   TreeNode *left,*right;
;
int ans=0;//统计数值之和

void build(TreeNode * &T)

    int x;
    cin>>x;
    if(x==-1)
        T==NULL;
        return ;
    
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);


void DFS(TreeNode *T,TreeNode *fa,TreeNode *gfa)//进行中序遍历

    if(!T) return;
    DFS(T->left,T,fa);
    //祖父结点存在且为偶数
    if(gfa&&gfa->val%2==0) ans+=T->val;
    DFS(T->right,T,fa);


int main()

    TreeNode * T=NULL;
    build(T);
    DFS(T,NULL,NULL);
    cout<<ans<<endl;
    return 0;

1369: 二叉树的最大深度

题目描述

给定一个二叉树，找出其最大深度。
最大深度是从根节点到最远叶子节点的最长路径上的节点数量。

输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

输出一行代表二叉树的最大深度。

样例输入

1 2 -1 -1 3 4 -1 -1 -1

样例输出

#include<bits/stdc++.h>
using namespace std;
const int N=100;

struct TreeNode 
   int val;
   TreeNode *left,*right;
;

void build(TreeNode * &T)

    int x;
    cin>>x;
    if(x==-1)
        T==NULL;
        return ;
    
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);


int Height(TreeNode *T,int h)

    if(T==NULL) return h;
    return max(Height(T->left,h+1),Height(T->right,h+1));


int main()

    TreeNode * T=NULL;
    build(T);
    cout<<Height(T,0)<<endl;
    return 0;

1370: 高度平衡的二叉树

题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。
一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。

输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

若是则输出YES，否则输出NO。

样例输入

1 2 -1 -1 3 4 -1 -1 -1

样例输出

YES

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//用flag标记二叉树是否平衡，对每个结点计算两个子树的高度差
struct TreeNode 
   int val;
   TreeNode *left,*right;
;
int flag=1;
void build(TreeNode * &T)

    int x;
    cin>>x;
    if(x==-1)
        T==NULL;
        return ;
    
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);


int Height(TreeNode *T,int h)

    if(T==NULL) return h;
    return max(Height(T->left,h+1),Height(T->right,h+1));


void Judge(TreeNode *T)

    if(!flag||T==NULL) return;
    if(abs(Height(T->left,0)-Height(T->right,0))>1) flag=0;
    //继续递归判断左右子树
    Judge(T->left);
    Judge(T->right);


int main()

    TreeNode * T=NULL;
    build(T);
    Judge(T);
    if(flag)
        printf("YES\\n");
    else
        printf("NO\\n");
    return 0;

1371: 求根到叶子结点数字之和

题目描述

给定一个二叉树，它的每个结点都存放一个1-9的数字，每条从根到叶子节点的路径都代表一个数字。
例如，从根到叶子节点路径 1->2->3 代表数字 123。
计算从根到叶子节点生成的所有数字之和，答案保证在int范围。

输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

输出根到叶子节点生成的所有数字之和。

样例输入

1 2 -1 -1 3 4 -1 -1 -1

样例输出

#include<bits/stdc++.h>
using namespace std;
const int N=100;
//用变量sum来统计所有数字之和，每次递归到了根节点，就把数字加到sum中，然后结束递归
struct TreeNode 
   int val;
   TreeNode *left,*right;
;
int sum=0;
void build(TreeNode * &T)

    int x;
    cin>>x;
    if(x==-1)
        T==NULL;
        return ;
    
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);


void Plus(TreeNode *T,int ans)

    //如果为叶子结点，结束递归
    if(T->left==NULL&&T->right==NULL) sum+=ans*10+T->val;
    //否则继续在左右子树递归查找叶子结点
    if(T->left!=NULL) Plus(T->left,ans*10+T->val);
    if(T->right!=NULL) Plus(T->right,ans*10+T->val);


int main()

    TreeNode * T=NULL;
    build(T);
    Plus(T,0);
    cout<<sum<<endl;
    return 0;

1372: 找树左下角的值

题目描述

给定一个二叉树，在树的最后一行找到最左边的值。

输入

输入一行，按照先序输入一棵二叉树，其中空节点用 -1 表示。

输出

输出树的最后一行最左边的值。

样例输入

1 2 -1 -1 3 4 -1 -1 -1

样例输出

#include<bits/stdc++.h>
using namespace std;
//按照先序遍历遍历整棵树，保存深度最深的第一个遍历到的叶子结点的值
const int N=100;
struct TreeNode 
   int val;
   TreeNode *left,*right;
;
int H=0,x;
void build(TreeNode * &T)

    int x;
    cin>>x;
    if(x==-1)
        T==NULL;
        return ;
    
    T=new TreeNode;
    T->val=x;
    T->left=T->right=NULL;
    build(T->left);
    build(T->right);


void findk(TreeNode *T,int h)

    //如果是叶子结点
    if(T->left==NULL&&T->right==NULLPPOJ刷题-2
 PPOJ刷题-2
 PPOJ刷题-1
 PPOJ刷题-1
 PPOJ刷题-1
 二叉树经典题之二叉树最近公共祖先（LeetCode）