一些结论总结
Posted Flame♡
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一些结论总结相关的知识,希望对你有一定的参考价值。
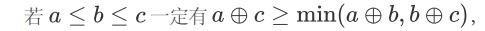
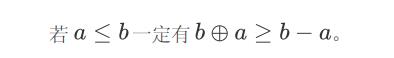


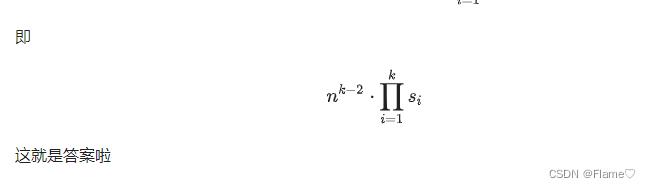
一个长度为
n
n
n的数列,里面可以任意填充
[
1
,
n
]
[1,n]
[1,n],长度为
k
k
k的最长上升子序列的期望个数是
(
n
k
)
/
k
!
\\binomnk/k!
(kn)/k!的 据说在根号的时候复杂度最大…
由上面得知的结论是最长上升子序列的期望是 n \\sqrtn n
也就是一个随机数列大概会由 n \\sqrtn n个长度为 n \\sqrtn n的最长上升子序列构成)
n n n 个点的有根二叉树的数量是 f n = ∑ i = 1 n − 1 f i f n − i − 1 f_n=\\sum\\limits_i=1^n-1f_if_n-i-1 fn=i=1∑n−1fifn−i−1
对应就是卡特兰数
f n f_n fn 的叶子数 g n = n ∗ f n − 1 g_n=n*f_n-1 gn=n∗fn−1
下图是求
n
!
n!
n! 里2的因子数目

证明
所以组合数是奇数当且仅当满足 n-a=m-b+(n-m)-c
即 a=b+c
即 n n n& m = = m m==m m==m
或者 m m m& ( n − m ) = = 0 (n-m)==0 (n−m)==0
(因为两个and=0说明没有位置重叠相加不存在进位 又因为两个相加要和n相等 所以只能是对应位置相等)
这个东西可以用来求网格图上路径数的奇偶性
学习资料:
以上是关于一些结论总结的主要内容,如果未能解决你的问题,请参考以下文章