[LeetCode] 42. Trapping Rain Water 收集雨水
Posted 轻风舞动
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[LeetCode] 42. Trapping Rain Water 收集雨水相关的知识，希望对你有一定的参考价值。
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
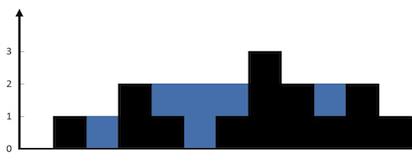
The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!
Example:
Input: [0,1,0,2,1,0,1,3,2,1,2,1] Output: 6
解法1：双指针Two Pointers，left和right分别指向数组的头尾，从两边向中间扫描，在当前两指针的范围内，先比较两头找出较小值，如果较小值是left指向的值，则从左向右扫描，如果较小值是right指向的值，则从右向左扫描，若遇到的值比当较小值小，则将差值存入结果，如遇到的值大，则重新确定新的窗口范围，迭代直至left和right指针重合。
对于任何一个坐标，检查其左右的最大坐标，然后相减就是容积。所以，
1. 从左往右扫描一遍，对于每一个坐标，求取左边最大值。
2. 从右往左扫描一遍，对于每一个坐标，求最大右值。
3. 再扫描一遍，求取容积并加和。
2和3可以合并成一个循环，公式：H[i] = min(Max(Array[j] ), Max(Array[k])) – Array[i] where j < i and k > i
解法2：栈stack
Follow up:
不求所有容积，而是求容积中的最大值。这样就类似于Container With Most Water，但是有不同的地方，这题里面每一个坐标本身是占体积的。所以从两边往中间扫的时候，根本不知道中间坐标共占用了多少体积。
Java:
public class Solution {
public int trapRainWater(int[] heights) {
if (heights.length == 0) {
return 0;
}
int[] maxHeights = new int[heights.length + 1];
maxHeights[0] = 0;
for (int i = 0; i < heights.length; i++) {
maxHeights[i + 1] = Math.max(maxHeights[i], heights[i]);
}
int max = 0, area = 0;
for (int i = heights.length - 1; i >= 0; i--) {
area += Math.min(max, maxHeights[i]) > heights[i]
? Math.min(max, maxHeights[i]) - heights[i]
: 0;
max = Math.max(max, heights[i]);
}
return area;
}
}
Java: 参考
public class Solution {
public int trap(int[] height) {
Stack<Integer> st = new Stack<Integer>();
if(height.length == 0)
return 0;
int i = 0;
int j = height.length - 1;
int ans = 0;//返回的答案
int secHight = 0;//第二个高度（最高的那个不动）
while(i < j){
if(height[i] < height[j]){
secHight = Math.max(secHight,height[i]);
//因为长度为1，高度也就是面积值，如果height[i]==secHight,则新增面积为0
ans += secHight - height[i];
i++;
}else{
secHight = Math.max(secHight,height[j]);
//因为长度为1，高度也就是面积值，如果height[i]==secHight,则新增面积为0
ans += secHight - height[j];
j--;
}
}
return ans;
}
}
Python:
class Solution:
# @param A, a list of integers
# @return an integer
def trap(self, A):
result = 0
top = 0
for i in xrange(len(A)):
if A[top] < A[i]:
top = i
second_top = 0
for i in xrange(top):
if A[second_top] < A[i]:
second_top = i
result += A[second_top] - A[i]
second_top = len(A) - 1
for i in reversed(xrange(top, len(A))):
if A[second_top] < A[i]:
second_top = i
result += A[second_top] - A[i]
return result
Python:
# Time: O(n)
# Space: O(n)
class Solution2:
# @param A, a list of integers
# @return an integer
def trap(self, A):
result = 0
stack = []
for i in xrange(len(A)):
mid_height = 0
while stack:
[pos, height] = stack.pop()
result += (min(height, A[i]) - mid_height) * (i - pos - 1)
mid_height = height
if A[i] < height:
stack.append([pos, height])
break
stack.append([i, A[i]])
return result
Python: wo
class Solution(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
if not height:
return 0
res = 0
left, right = 0, len(height) - 1
left_max, right_max = 0, 0
while left < right:
if height[left] < height[right]:
left_max = max(left_max, height[left])
left += 1
res += max(0, left_max - height[left])
else:
right_max = max(right_max, height[right])
right -= 1
res += max(0, right_max - height[right])
return res
C++:
// Time: O(n)
// Space: O(1)
class Solution {
public:
int trap(vector<int>& height) {
if (height.empty()) {
return 0;
}
int i = 0, j = height.size() - 1;
int left_height = height[0];
int right_height = height[height.size() - 1];
int trap = 0;
while (i < j) {
if (left_height < right_height) {
++i;
// Fill in the gap.
trap += max(0, left_height - height[i]);
// Update current max height from left.
left_height = max(left_height, height[i]);
}
else {
--j;
// Fill in the gap.
trap += max(0, right_height - height[j]);
// Update current max height from right.
right_height = max(right_height, height[j]);
}
}
return trap;
}
};
C++:
int trap(vector<int>& height) {
int l = 0, r = height.size()-1, level = 0, water = 0;
while (l < r) {
int lower = height[height[l] < height[r] ? l++ : r--];
level = max(level, lower);
water += level - lower;
}
return water;
}
C++:
#include <bits/stdc++.h>
using namespace std;
// two pointers
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size();
// Exceptional Case:
if(n <= 2){
return 0;
}
int ans = 0;
int left = 0, right = n - 1;
while(left < right){
int min_height = min(height[left], height[right]);
if(height[left] == min_height){
while(++left < right && height[left] <= min_height){
ans += (min_height - height[left]);
}
}
else if(height[right] == min_height){
while(left < --right && height[right] <= min_height){
ans += (min_height - height[right]);
}
}
}
return ans;
}
};
类似题目：
[LeetCode] 11. Container With Most Water 装最多水的容器
[LeetCode] 407. Trapping Rain Water II 收集雨水 II
All LeetCode Questions List 题目汇总
以上是关于[LeetCode] 42. Trapping Rain Water 收集雨水的主要内容，如果未能解决你的问题，请参考以下文章
leetcode42 Trapping Rain Water
LeetCode-42-Trapping Rain Water
leetcode 42. Trapping Rain Water
LeetCode 42. Trapping Rain Water