二叉树的操作

Posted 2023-02-25 勇士后卫头盔哥

二叉树的比较与相加

二叉树的克隆操作
克隆操作就是将当前的二叉树复制一份出来,其复制接口的返回值为堆空间中的一颗新二叉树,这个二叉树的地址是不一样的,但是这颗树的其他属性和数据元素在对应位置都是相当的,接口的定义如下所示

sharedPointer <BTree<T>> clone()const

设计思路
在堆空间里面先创建一个二叉树结点出来,然后把数据元素复制到新创建的二叉树结点中,接下来就递归的克隆左子树和右子树,然后指定左右子树的父亲,也就是新创建出来的结点,递归公式如下

             return NULL;                     node == NULL
clone(node)
             n = NewNode();
             n->value = node->value;
             n->left  = clone(node->left);    node != NULL
             n->right = clone(node->right);

代码实现

protected:
BTreeNode<T>*  clone(BTreeNode<T>* node)const

    BTreeNode<T>* ret = NULL;
    if(node!=NULL)
    
         ret = BTreeNode<T>::NewNode();
         if(ret!=NULL)
         
             ret->value = node->value;
             ret->l_pointer = clone(node->l_pointer);
             ret->r_pointer = clone(node->r_pointer);
             if(ret->l_pointer!=NULL)
             
                ret->l_pointer->parent = ret;
             
             if(ret->r_pointer!=NULL)
             
                ret->r_pointer->parent = ret;
             
         
         else
         
           THROW_EXCEPTION(NoEnougMemoryException,"No EnoungMemory");
         
    
    return ret;

public:
SharedPointer < BTree<T> > clone()const

    BTree<T>* ret = new BTree<T>();
    if(ret!=NULL)
    
        ret->m_root = clone(root());
    
    else
    
        THROW_EXCEPTION(NoEnougMemoryException,"No enoug memory to malloc");
    
   return ret;

二叉树比较操作

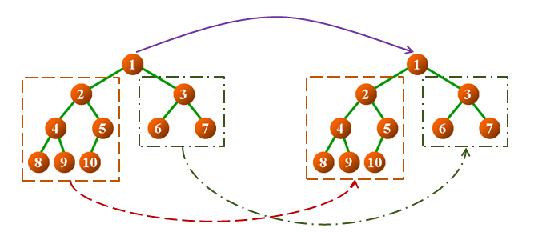
二叉树比较操作就是判断两个二叉树中的数据元素是否对应相等,就是两个树的根节点数据元素,左子树,右子树对应相等,因为引入了比较操作,所以我们得重载比较操作符,可以看出比较也是一个递归调用的过程,递归公式如下所示

                 return true;          lh==rh
                 return false;         lh == 0&& rh!=0
                 retunr false;         lh != 0&& rh==0
equal(rh,lh)
                 lh->value==rh->value&&
                 equal(lh->left,rh->left)&&   lh!=0&&rh!=0
                 equal(lh->right,rg->right)

代码:

protected:
bool operator ==(const BTree<T>* btree)

    return equal(this->root(),btree->root());

bool operator !=(const BTree<T>* btree)

    return !(this==btree);

public:
bool equal(BTreeNode<T>* lh,BTreeNode<T>* rh)

    if(lh==rh)
    
        return true;
    
    else if((lh!=NULL)&&(rh!=NULL))
    
        return (lh->value==rh->value)&&equal(lh->l_pointer,rh->l_pointer)&&equal(lh->r_pointer,rh->r_pointer);
    
    else
    
         return false;
    

二叉树的相加操作

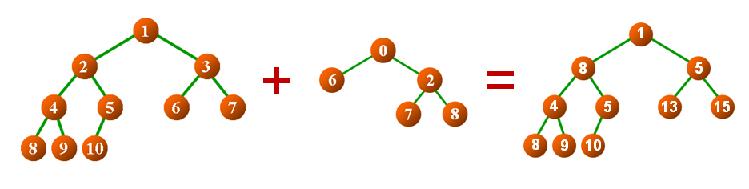
相加操作就是将当前二叉树与参数btree中的数据元素在对应位置处相加,返回值为堆空间中的一颗新二叉树,当然对于二叉树来说它还有一些特殊的结点,比如上图中的2号结点,6号结点相加操作,需要将2号结点的左子树赋值结果二叉树对应结点的左子树,同样的道理2号结点的右子树也是同样的操作,将lh为根节点的二叉树与递归公式如下所示

             clone(rh)                            lh==0&&rh!=0
           
add(lh,rh)   clone(lh)                            lh!=0&&rh==0
             
             n =  NewNode();
             n->value = lh->value + rh->value;
             n->left  = add(lh->left,rh->left);   lh!=0&&rh!=0
             n->right = add(lh->right,rh->rigth);

代码

  protected:
  BTreeNode<T>* add(BTreeNode<T>* lh,BTreeNode<T>* rh)
  
      BTreeNode<T>* ret = NULL;
      if((lh!=NULL)&&(rh==NULL))
      
          ret = clone(lh);
      
      else if((lh==NULL)&&(rh!=NULL))
      
          ret =  clone(rh);
      
      else if((lh!=NULL)&&(rh!=NULL))
      
          ret = BTreeNode<T>::NewNode();
          if(ret!=NULL)
          
              ret->value        = lh->value+rh->value;
              ret->l_pointer    = add(lh->l_pointer,rh->l_pointer);
              ret->r_pointer    = add(lh->r_pointer,rh->r_pointer);
              if(ret->l_pointer!=NULL)
              
                 ret->l_pointer->parent = ret;
              
              if(ret->r_pointer!=NULL)
              
                 ret->r_pointer->parent = ret;
              
          
          else
          
              THROW_EXCEPTION(NoEnougMemoryException,"no EnougMemory Exception");
          
      
      return ret;
  
  public:
  SharedPointer < BTree<T> > add(const BTree<T>& btree)
 
      BTree<T>* ret = new BTree<T>();
      if(ret!=NULL)
      
          ret->m_root = add(root(),btree.root());
      
      else
      
          THROW_EXCEPTION(NoEnougMemoryException,"no EnougMemory.....");
      
      return ret;
  

实验代码

int main()

  BTree<int> bt;
  BTreeNode<int>* n = NULL;
  bt.insert(1,NULL);

  n = bt.find(1);
  bt.insert(2,n);
  bt.insert(3,n);


  n = bt.find(2);
  bt.insert(4,n);
  bt.insert(5,n);

  n = bt.find(4);
  bt.insert(8,n);
  bt.insert(9,n);

  n = bt.find(5);
  bt.insert(10,n);

  n=bt.find(3);
  bt.insert(6,n);
  bt.insert(7,n);
  SharedPointer < BTree<int> > clonenode   = bt.clone();
  BTree<int> nbt;
  nbt.insert(0,NULL);

  n = nbt.find(0);
  nbt.insert(6,n);
  nbt.insert(2,n);

  n = nbt.find(2);
  nbt.insert(7,n);
  nbt.insert(8,n);

  SharedPointer < BTree<int> > r = bt.add(nbt);

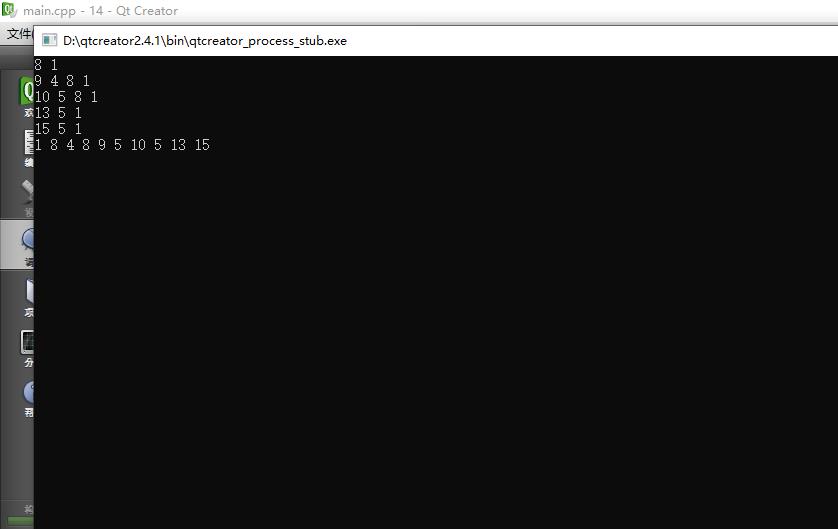
  int a[] = 8,9,10,13,15;
  for(int i =0;i<5;i++)
  
      TreeNode<int>* node = r->find(a[i]);
      while(node)
      
          cout<<node->value<<" ";
          node = node->parent;
      
      cout<<endl;
  
  SharedPointer < Aarry<int> > tr = r->traversal(PreOrder);//先序遍历
  for(int i =0;i<tr->length();i++)
  
      cout<<(*tr)[i]<<" ";
  
  cout<<endl;
  //cout<<(bt==*clonenode)<<endl;

  return 0;